АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Скалярное произведение

Понятие скалярного произведения вводилось в школьном курсе геометрии. Напомним его и рассмотрим свойства этого произведения.

Определение 17. Скалярным произведением двух векторов а и b называется число (a, b) равное произведению модулей векторов а и b на косинус угла между ними, т.е.

(a, b) = | a | ∙ | b | ∙ cos φ,

где φ – угол между векторами а и b.

Определение 18. Если угол между векторами прямой, то векторы называются ортогональными.

Скалярное произведение нулевого вектора на любой вектор считается равным нулю.

Свойства скалярного произведения:

1. (a, b) = (b, a) (коммутативность);

2. (a, b) = 0 тогда и только тогда, когда выполняется одно из условий:

а) а = 0;

б) b = 0;

в) cos φ = 0, т. е. а и b ортогональны;

3. (a, а) = | а |², т. е. скалярный квадрат вектора равен квадрату модуля этого вектора. Действительно, в этом случае φ = 0 и cos φ = 0, тогда

(a, а) = | a | ∙ | а | ∙ cos φ = | а |²;

4. (a, а) = 0 тогда и только тогда, когда а – нулевой вектор;

5. векторы ортонормированного базиса удовлетворяют соотношениям:

(е ₁, е ₁) = (е ₂, е ₂) = (е ₃, е ₃) = 1,

(е ₁, е ₂) = (е ₁, е ₃) = (е ₂, е ₃) = 0;

6. если λ – число, то (λ a, b) = λ(a, b), т.е. числовой множитель можно выносить за знак скалярного произведения;

7. (a + b, с) = (a, с) + (b, c) (дистрибутивность);

8. координаты любого вектора в прямоугольной системе координат равны скалярным произведениям этого вектора на базисные вектора.

Докажем последнее свойство. Пусть вектор а имеет в некотором базисе е ₁, е ₂, е ₃ разложение

а = а ₁ е ₁ + а ₂ е ₂ + а ₃ е ₃.

Рассмотрим скалярное произведение вектора на базисный вектор, используя при этом свойство дистрибутивности:

(а, е ₁) = (а ₁ е ₁ + а ₂ е ₂ + а ₃ е ₃, е1) =

= (а ₁ е ₁, е ₁) + (а ₂ е ₂, е ₁) + (а ₃ е ₃, е ₁) = а ₁(е ₁, е ₁) + а ₂(е ₂, е ₁) + а ₃(е ₃, е ₁).

Если базис ортогонален, то

(е ₁, е ₂) = (е ₃, е ₁) = 0, (е ₁, е ₁) = | е ₁|².

Получаем, что скалярное произведение вектора на базисный вектор равно

(а, е ₁) = а ₁ | е ₁|²,

.

Аналогично, другие координаты вектора:

, .

Если базис е ₁, е ₂, е ₃ не только ортогонален, но еще и нормирован, т.е. | е ₁| = | е ₂| = | е ₃| = 1, то

а ₁ = (а, е ₁), а ₂ = (а, е ₂), а ₃ = (а, е ₃).

Таким образом, свойство 8 доказано.

Найдем выражение скалярного произведения через координаты сомножителей.

Пусть в некотором базисе е ₁, е ₂, е ₃ векторы а и b имеют следующие координаты

а (а ₁, а ₂, а ₃), b (b ₁, b ₂, b ₃).

Найдем их скалярное произведение (a, b), для чего воспользуемся свойствами 6 и 7.

(a, b) = (а ₁ е ₁ + а ₂ е ₂ + а ₃ е ₃, b ₁ е ₁ + b ₂ е ₂ + b ₃ е ₃) =

= а ₁ b ₁(е ₁, е ₁) + а ₁ b ₂(е ₁, е ₂) + а ₁ b ₃(е ₁, е ₃) +

+ а ₂ b ₁(е ₂, е ₁) + а ₂ b ₂(е ₂, е ₂) + а ₂ b ₃(е ₂, е ₃) +

+ а ₃ b ₁(е ₃, е ₁) + а ₃ b ₂(е ₃, е ₂) + а ₃ b ₃(е ₃, е ₃).

Если базис е ₁, е ₂, е ₃ произвольный, то данная формула является окончательной. Если базис е ₁, е ₂, е ₃ ортогонален, т. е.

(е ₁, е ₂) = (е ₁, е ₃) = (е ₂, е ₃) = 0,

то формула примет вид:

(a, b) = а ₁ b ₁ (е ₁, е ₁) + а ₂ b ₂ (е ₂, е ₂) + а ₃ b ₃ (е ₃, е ₃) =

= а ₁ b ₁ | е ₁|² + а ₂ b ₂ | е ₂|² + а ₃ b ₃ | е ₃|².

Если кроме ортогональности векторов потребуем, чтобы их длины равнялись единице, т. е. базис е ₁, е ₂, е ₃ являлся бы ортонормированным, то формула будет иметь вид:

(a, b) = а ₁ b ₁ + а ₂ b ₂ + а ₃ b ₃ .

Это формула выражения скалярного произведения через координаты сомножителей в ортонормированном базисе.

Учитывая, что

(a, b) = | a | ∙ | b | ∙ cos φ,

, ,

получим формулу для нахождения угла между векторами

.

Таким образом, скалярное произведение применяется, когда нужно найти угол между векторами, определить являются ли данные векторы ортогональными.

Дата добавления: 2015-01-18 | Просмотры: 665 | Нарушение авторских прав
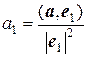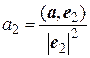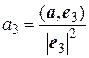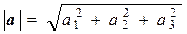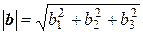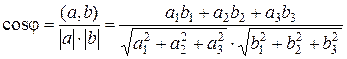