 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Взаимное расположение прямых и плоскостей1. прямые на плоскости Рассмотрим расположение двух прямых на плоскости. Они могут быть параллельны или пересекаться. Совпадающие прямые будем рассматривать как частный случай параллельных прямых. Перпендикулярные прямые – частный случай пересекающихся прямых. Очевидно, что две прямые параллельны, если у них коллинеарны направляющие вектора или, соответственно, нормальные вектора. В остальных случаях прямые пересекаются.
Полученная формула
определяет один из углов между прямыми, другой угол равен π – φ. Пример 1. Прямые заданы уравнениями y = 2 x + 3 и y = –3 x + 2. Найти угол между этими прямыми. Очевидно, что k 1 = 2, k 2 = –3, поэтому
Таким образом, один из углов между данными прямыми равен Если прямые заданы общими уравнениями: A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0, тогда
Получили аналогичную формулу для нахождения угла:
Для простоты можно условиться под углом φ между двумя прямыми понимать острый положительный угол. Тогда тангенс этого угла будет всегда положительным. Поэтому для острого угла φ получаем:
Пример 2. Определить угол между прямыми 2 x – 3 y + 7 = 0 и 4 x – 8 y + 9 = 0. По последней формуле имеем
Очевидно, что для параллельных прямых тангенс угла между ними равен нулю. Поэтому для прямых, заданных уравнениями с угловыми коэффициентами y = k 1 x + b 1, y = k 2 x + b 2 получим A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 получаем
Значит, A 1 B 2 – A 2 B 1 = 0 – условие параллельности прямых. Учитывая, что для прямой Ax + By + C = 0 вектор q = (– B, A) можно рассматривать как направляющий, то аналогичные формулы можно вывести, рассматривая угол между прямыми, как угол между их направляющими векторами. Очевидно, чтобы угол между прямыми был прямой, т.е. они были перпендикулярны, необходимо, чтобы были перпендикулярны их нормали или, соответственно, их направляющие вектора. Для прямых A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 получаем: (n 1, n 2) = 0 или A 1 A 2 + B 1 B 2 = 0. Это условие перпендикулярности прямых. Преобразуем последнее уравнение, разделив обе его части на B 1 B 2, получаем
Заменим 1 + k 1 k 2 = 0 или k 1 k 2 = –1. Полученное соотношение k 1 k 2 = –1 дает условие перпендикулярности прямых, заданных уравнениями с угловыми коэффициентами. Пример 3. Показать, что прямые 2 x – 4 y + 1 = 0 и – x + 2 y + 3 = 0 параллельны. Действительно A 1 = 2, B 2 = –4 и A 2 = –1, B 2 = 2. Подставим эти значения в условие параллельности прямых A 1 B 2 – A 2 B 1 = 0: 2 ∙ 2 – (–1) ∙ (–4) = 0. Получим верное тождество. Пример 4. Показать, что прямые 3 x – 5 y + 7 = 0 и 10 x + 6 y – 3 = 0 перпендикулярны. Приведем уравнения прямых к уравнениям с угловыми коэффициентами: 5 y = 3 x + 7 => 6 y = –10 x + 3 => Следовательно,
Пусть заданы две прямые A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0. Пусть известно, что они параллельны, т.е. A 1 B 2 – A 2 B 1 = 0. Если координаты нормального вектора n 2 ненулевые, то это условие можно переписать:
Это условие параллельности прямых. Если пропорциональны и свободные члены этих уравнений, то прямые совпадают:
Это условие совпадения прямых.
2. плоскости Очевидно, что две плоскости могут быть параллельны или пересекаться. Совпадение двух плоскостей будем рассматривать как частный случай параллельных плоскостей. Частным случаем пересекающихся плоскостей являются перпендикулярные плоскости. Угол между плоскостями – это угол между их нормальными векторами. Следовательно, если две плоскости заданы общими уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0, то угол φ между плоскостями можно найти как угол между векторами n 1(A 1, B 1, C 1) и n 2(A 2, B 2, C 2), используя скалярное произведение:
Это формула нахождения угла между плоскостями. Очевидно, что если мы хотим найти острый угол между плоскостями, то cosφ > 0 и дробь берем со знаком плюс. Если две плоскости перпендикулярны, то перпендикулярны и их нормальные вектора и, значит, их скалярное произведение равно нулю (n 1, n 2) = 0 или A 1 A 2 + B 1 B 2 + C 1 C 2 = 0. Это условие перпендикулярности плоскостей. Две плоскости параллельны, если параллельны их нормальные вектора, а это значит, их векторное произведение равно нулю:
Значит, условие параллельности плоскостей можно записать в виде:
т.е. координаты нормалей пропорциональны. Если все координаты вектора n 2 отличны от нуля, условие параллельности можно записать иначе:
Выясним, при каком условии плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 совпадают. Для решения этой задачи заметим, что мы рассматриваем совпадение как частный случай параллельности. Поэтому должно выполняться условие
С другой стороны, ввиду совпадения плоскостей, координаты (x, y, z) в обоих уравнениях принимают одни и те же значения. Умножая уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 на общую величину из соотношения
получаем μ A 2 x + μ B 2 y + μ C 2 z + μ D 2 = 0 или Сокращая выражения, получаем A 1 x + B 1 y + C 1 z + μ D 2 = 0. (**) Вычтем из полученного уравнения (**) уравнение первой плоскости A 1 x + B 1 y + C 1 z + D 1 = 0, получим D 2μ – D 1 = 0 и, следовательно, Итак, пропорция (*) дополняется еще одним звеном и принимает вид
Обратно, при соблюдении условия (***) уравнения A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 действительно изображают одну и ту же плоскость, т.к. первое уравнение получается из второго умножением на общую величину μ. Следовательно, условие (***) – условие совпадения плоскостей. Пример 5. Убедимся, что уравнения 2 x – 3 y + z – 4 = 0 и –4 x + 6 y – 2 z + 8 = 0 задают одну и ту же прямую. Запишем соответствующее соотношение
Каждая из дробей при сокращении равна (–1/2) и, следовательно, условие совпадения плоскостей выполнено.
Заметим, что условие
предполагает ненулевые коэффициенты второй плоскости. Для того чтобы избежать этого ограничения, данные условия можно записать следующим образом
Эти условия также представляют собой условия совпадения плоскостей. 3. прямые в пространстве Две прямые в пространстве могут пересекаться, быть параллельны и скрещиваться. Угол между прямыми в пространстве – это угол между направляющими векторами. Две прямые образуют два угла в сумме составляющие 180º. Косинусы обоих углов отличаются только знаком. Если требуется найти острый угол, то косинус берут со знаком плюс. Пусть даны две прямые, заданные каноническими уравнениями:
Направляющие векторы q (q 1, q 2, q 3) и s (s1, s 2, s 3) образуют угол, косинус которого можно найти по формуле
Таким образом, эту формулу можно рассматривать и как формулу угла между двумя прямыми в пространстве. Очевидно, что прямые параллельны, если их направляющие вектора коллинеарны. Условие коллинеарности векторов можно записать в виде:
или, приравнивая их к нулю координаты векторного произведения [ q, s ], получим
Если координаты направляющего вектора s (s 1, s 2, s 3) отличны от нуля, то условие коллинеарности векторов можно записать в более удобной форме:
Последние два соотношения можно рассматривать как условие параллельности двух прямых. Очевидно, если направляющие вектора двух прямых коллинеарны, а координаты начальной точки одной прямой удовлетворяют уравнению другой прямой, то прямые совпадают. Пример 1. Покажем, что уравнения
задают одну и ту же прямую. Действительно, направляющие вектора этих прямых коллинеарны
Покажем, что координаты начальной точки второго уравнения (3;5;2) удовлетворяют первому уравнению
Таким образом, эти прямые параллельны и проходят через одну и ту же точку и, следовательно, эти прямые совпадают. Если прямые пересекаются или скрещиваются под прямым углом, то скалярное произведение направляющих векторов будет равно нулю. Например, для прямых
условие перпендикулярности прямых будет иметь вид: q 1 s 1 + q 2 s 2 + q 3 s 3 = 0. Для того чтобы определить являются ли две непараллельные прямые пересекающимися или скрещивающимися, рассмотрим их параметрические уравнения:
Очевидно, если точка пересечения существует, то найдутся такие значения параметров t 1 и t 2, для которых будут выполняться равенства
и, следовательно, система будет иметь решение. Подставляя полученные значения t 1 и t 2 в параметрические уравнения, получим координаты точки пересечения. Если система несовместна, то прямые не пересекаются и, значит, являются скрещивающимися. Пример 2. Покажем, что прямые
пересекаются, и найдем координаты точки пересечения. Перейдем от канонических уравнений к параметрическим:
Аналогично для второй прямой:
Приравняем соответствующие координаты для систем, получим
Решая последнюю систему, получим t = 1, t 1 = 0. Подставляя значение параметров в параметрические уравнения прямых, получаем координаты точки пересечения: x = 3, y = 5, z = 2.
Рассмотрим расположение в пространстве прямой и плоскости. Прямая и плоскость либо пересекаются, либо параллельны. Очевидно, что плоскость Ax + By + Cz + D = 0 и прямая, заданная уравнением
параллельны тогда и только тогда, когда вектор нормали n (A, B, C) перпендикулярен направляющему вектору прямой q (q 1, q 2, q 3). И, значит, их скалярное произведение равно нулю: Aq 1 + Bq 2 + Cq 3 = 0. Это условие параллельности прямой и плоскости. Если Aq 1 + Bq 2 + Cq 3 ≠ 0, то прямая и плоскость пересекаются. Для того чтобы найти координаты точки пересечения, запишем параметрические уравнения прямой:
Подставим полученные выражения для x, y и z в уравнение плоскости, получим A (q 1 t + x 1) + B (q 2 t + y 1) + C (q 3 t + z 1) + D = 0. Решаем полученное уравнение относительно t: (Aq 1 + Bq 2 + Cq 3) t = – Ax 1 – By 1 – Cz 1 – D,
Подставляем полученное значение t в параметрические уравнения, найдем координаты точки пересечения прямой и плоскости. Пример 3. Найдем точку пересечения плоскости 5 x + 2 y – 3 z + 4 = 0 и прямой, заданной уравнением
Перепишем уравнение прямой в виде:
Следовательно, параметрические уравнения прямой имеют вид:
Подставим полученные выражения в уравнение плоскости, получим: 5(2 t + 1) + 2(4 t + 3) – 3(3 t + 2) + 4 = 0, 10 t + 5 + 8 t + 6 – 9 t – 6 + 4 = 0, 9 t + 9 = 0, t = –1. Подставим t = –1 в параметрические уравнения прямой, найдем координаты: x = –2 + 1 = –1, y = –4 + 3 = –1, z = –3 + 2 = –1. Получили координаты точки пересечения М 1(–1; –1; –1) прямой и плоскости. Сделаем проверку, подставив координаты М 1(–1; –1; –1) в уравнение плоскости: –5 – 2 + 3 + 4 = 0. Убеждаемся, что М 1 лежит в плоскости. Подставим координаты М 1 в каноническое уравнение прямой:
Следовательно, точка принадлежит прямой. Итак, точка М 1(–1; –1; –1) является точкой пересечения прямой и плоскости.
Вопросы для самопроверки 1. Какими уравнениями задается прямая на плоскости? 2. Как можно задать плоскость? 3. Какие уравнения задают прямую в пространстве? 4. Какие возможны взаимные расположения прямой и плоскости? Дата добавления: 2015-01-18 | Просмотры: 1956 | Нарушение авторских прав |
Найдем угол между двумя прямыми. Пусть уравнение прямой L 1 имеет вид y = k 1 x + b 1, где k 1 = tgα1, а уравнение прямой L 2: y = k 2 x + b 2, где k 2 = tgα2.
Из рис. 38 видно, что α2 = φ + α1 и, значит, φ = α2 – α1. Следовательно,
.
.
, другой угол равен 
.
и 
. Подставим значения k 1 и k 2 в формулу угла между прямыми и получим:
.
.
.
.
или 
.
на k 1 и 
на k 2, получим
;
.
и 
и, значит, k 1 k 2 = –1. Данные прямые перпендикулярны.
.
.
.
.
,
,
.
.
. (***)
.
и 
.
,
.
и 
.
или 
.
и 
и 
=> 
=> 
=> 
=> 
=> 
=> 
.
.
=> 
.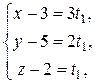