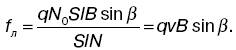АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Магнитное поле

Магнитным полем называют всю материю, посредством которой осуществляется силовое воздействия на движущиеся электрические заряды, помещенные в поле, и другие тела, обладающие магнитным моментом. Для магнитного поля, как и для электростатического, имеется количественная характеристика – магнитный момент (векторная величина).

Магнитная индукция в некоторой точке поля равна отношению максимального вращающего момента, действующего на рамку с током в однородном магнитном поле, к магнитному моменту этой рамки. Единицей магнитного потока является вебер (Вб):

1Вб = 1Тлм2.

Тл – единица магнитной индукции (Тесла). Из формулы видно, что поток может быть как положительным, так и отрицательным.

Закон Ампера. Энергия контура с током в магнитном поле. Одним из главных проявлений магнитного поля является его силовое действие на движущиеся электрические заряды и токи. А. М. Ампером был установлен закон, определяющий это силовое воздействие.

В проводнике, находящемся в магнитном поле, выделим достаточно малый участок dI, который рассматривается как вектор, направленный в сторону тока. Произведение IdI называют элементом тока. Сила, действующая со стороны магнитного поля на элемент тока, равна:

dF = kIB sinb × dl,

где k – коэффициент пропорциональности; или в векторной форме

dF = ldl × B.

Эти соотношения выражают закон Ампера.

Сила, действующая согласно закону Ампера на проводник с током в магнитном поле, есть результат его воздействия на движущиеся электрические заряды, создающие этот ток. Сила, действующая на отдельный движущийся заряд, определяется отношением силы F, приложенной к проводнику с током, к общему числу N носителей тока в нем:

f _Л = F / N_(i)

Сила тока равна:

I = jS,

F = jSBL sinb,

где j – плотность тока. Получаем:

F = jSBL sin b = qnvSBL sinb2,

где n =N/ S I – концентрация частиц.

Подставляя последнее выражение к первому, получаем выражение для силы, действующей со стороны магнитного поля на отдельный движущийся электрический заряд и называемой силой Лоренца:

Направление силы Лоренца можно определить из векторной записи уравнения

f n = qvB.

Дата добавления: 2015-02-02 | Просмотры: 644 | Нарушение авторских прав