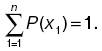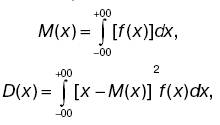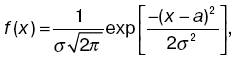АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Случайная величина. Закон распределения

Определение случайной величины. Многие случайные события могут быть оценены количественно как случайные величины. Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретные и непрерывные случайные величины.

Распределение дискретной случайной величины. Дискретная величина считается заданной, если указаны возможные ее значения и соответствующие им вероятности. Обозначим дискретную случайную величину х, ее значения х₁, х₂…, в вероятности: Р (х₁) =р₂, Р (х2) = р₂ и т. д.

Совокупность х и Р называется распределением дискретной случайной величины.

Так как все возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна единице:

Здесь предполагается, что дискретная случайная величина имеет n значений. Выражение называется условием нормировки.

Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины. Наиболее употребительные из них: 1) математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений;

2) дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Для непрерывной случайной величины математическое ожидание и дисперсия записываются в виде:

где f(x) – плотность вероятности или функция распределения вероятностей. Она показывает, как изменяется вероятность отнесения к интервалу dx случайной величины в зависимости от значения самой этой величины. Нормальный закон распределения. В теориях вероятностей и математической статистики, в различных приложениях важную роль играет нормальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность ее вероятности имеет вид:

где а = М(х) – математическое ожидание случайной величины;

σ – среднее квадратное отклонение; следовательно;

σ²– дисперсия случайной величины. Кривая нормального закона распределения имеет колоколообразную форму, симметричную относительно прямой х = а (центр рассеивания).

Дата добавления: 2015-02-02 | Просмотры: 717 | Нарушение авторских прав