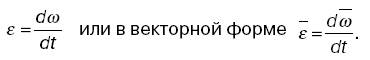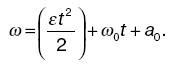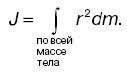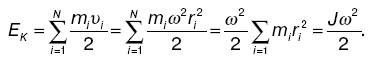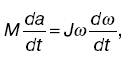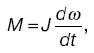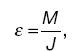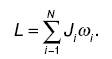АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Основы механики

Механикой называют раздел физики, в котором изучается механическое движение материальных тел. Под механическим движением понимают изменение положения тела или его частей в пространстве с течением времени.

Для медиков этот раздел представляет интерес по следующим причинам:

1) понимание механики движения целого организма для целей спортивной и космической медицины, механики опорно-двигательного аппарата человека – для целей анатомии и физиологии;

2) знание механических свойств биологических тканей и жидкостей;

3) понимание физических основ некоторых лабораторных методик, используемых в практике медико-биологических исследований, например центрифугирования.

Механика вращательного движения абсолютно твердого тела

Абсолютно твердым телом называют такое, расстояние между любыми двумя точками которого неизменно. При движении размеры и форма абсолютно твердого тела не изменяются. Быстрота вращения тела характеризуется угловой скоростью, равной первой производной от угла поворота радиус-вектора по времени:

ω = dt/da

Угловая скорость есть вектор, который направлен по оси вращения и связан с направлением вращения. Вектор угловой скорости в отличие от векторов скорости и силы является скользящим. Таким образом, задание вектора w указывает положение оси вращения, направление вращения и модуль угловой скорости. Быстрота изменения угловой скорости характеризуется угловым ускорением, равным первой производной от угловой скорости по времени:

Из этого видно, что вектор углового ускорения совпадает по направлению с элементарным, достаточно малым изменением вектора угловой скорости dw: при ускоренном вращении угловое ускорение направлено так же, как и угловая скорость, при замедленном вращении – противоположно ей. Приведем формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:

1) уравнение равномерного вращательного движения:

a = wt + a₀

где а₀ – начальное значение угла;

2) зависимость угловой скорости от времени в равномерном вращательном движении:

w = et + W₀,

где w₀ – начальная угловая скорость;

3) уравнение равнопеременного вращательного движения:

Основные понятия механики

Момент силы. Моментом силы относительно оси вращения называют векторное произведение радиус-вектора на силу:

M_i = r_i × F_i,

где r_i и F_i – векторы.

Момент инерции. Мерой инерции тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от распределения ее в пространстве относительно оси.

Моментом инерции тела относительно оси называют сумму моментов инерции материальных точек, из которых состоит тело:

Момент инерции сплошного тела обычно определяют интегрированием:

Момент импульсов тела относительно оси равен сумме моментов импульсов точек, из которых состоит данное тело:

Кинетическая энергия вращающего тела. При вращении тела его кинетическая энергия складывается

10б из кинетических энергий отдельных его точек. Для твердого тела:

Приравняем элементарную работу всех внешних сил при таком повороте к элементарному изменению кинетической энергии:

Mda = Jwdw,

откуда

сокращаем это равенство на ω:

откуда

Закон сохранения момента импульса. Если суммарный момент всех внешних сил, действующих на тело, равен нулю, то момент импульса этого тела остается постоянным. Этот закон справедлив не только для абсолютно твердого тела. Так, для системы, состоящей из N тел, вращающихся вокруг общей оси, закон сохранения момента импульса можно записать в форме:

Дата добавления: 2015-02-02 | Просмотры: 581 | Нарушение авторских прав