 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫЗадание 1. Найти область определения функции Решение. Функция
Задание 3. 1. Найти производные функций указанного порядка: а) б) Решение. а) Применим правило дифференцирования суммы
При дифференцировании первого слагаемого используем формулу
Для второго слагаемого применим формулу
Итак, в результате получим:
б) Замечая, что
Итак, в ответе получаем Найдем
Итак,
Задание 4.
Решение.
Пояснения к решению: 1) В числителе применили формулу сокращенного умножения 2) Поделив почленно числитель на знаменатель, представили подынтегральную функцию в виде суммы более простых функций. 3) Применили свойства неопределенного интеграла: интеграл от суммы функций равен сумме интегралов от каждой функции, а также вынесли постоянный множитель за знак интеграла. 4) Использовали таблицу основных интегралов. 2. Найти Решение. В этом интеграле надо сделать замену переменных.
Пояснения к решению: 1) Делаем замену переменных 2) Снова делаем замену переменных, возвращаясь к прежней переменной
4. Найти Решение. В этом случае необходимо применить формулу интегрирования по частям
Пояснения к решению: 1) Применили формулу интегрирования по частям. Это дало возможность понизить показатель степени степенной функции. 2) Еще раз применили формулу интегрирования по частям.
Задание 5.
Вычислим интеграл
Ответ:
Задание 6.
а) Вычислить площадь фигуры, ограниченной линиями:
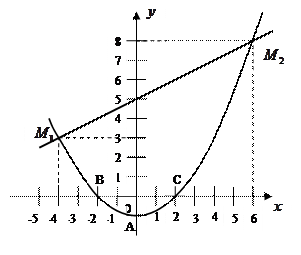
Решение. Построим фигуру, площадь которой требуется найти (рис. 2). Графиком функции
Таким образом, Найдём точки пересечения параболы с осью
Парабола пересекает ось абсцисс в точках Для построения прямой, заданной уравнением
Найдём точку пересечения прямой и параболы. Для этого решим совместно систему уравнений:
Рис. 2
Итак, прямая пересекает параболу в точках
где
так как прямая является верхней границей заштрихованной области, а парабола − нижней. Итак,
Ответ: Площадь фигуры, ограниченной линиями
б) Вычислить объём тела, образованного вращением вокруг оси
Решение. Объём тела, образованного вращением вокруг оси
. Выразим
получим пределы интегрирования
Тогда
Ответ: Объём тела, образованного вращением вокруг оси
Задание 7. Найти общее решение уравнения Решение. Разделив в этом уравнении переменные и интегрируя обе части, получим
Ответ: Задача 8. Группа студентов в течении недели осуществляет дежурство на 8 различных объектах. Сколькими способами можно составить расписание дежурств в субботу, если в этот день недели должно осуществляться дежурство только на 3 любых объектах? Решение. Количество вариантов дежурств на объектах в субботу равно числу размещений из восьми элементов по три элемента. Находим Ответ: Можно составить 336 различных вариантов дежурств на субботу на объектах. Задача 9. В полученной партии из 20 коробок лекарственных средств 5 коробок содержат брак. Для быстрого выяснения наличия брака в партии случайным образом вскрывают и обследуют 2 коробки. а) Найти вероятность того, что среди них окажется хотя бы одна браком. б) Найти вероятность этого же события, если обследовать 6 коробок. Решение. Обозначим через Аi событие, состоящее в том, что i -ая извлеченная коробка окажется с браком; через А – хотя бы одна из коробок содержит брак. Тогда а) Чтобы наступило событие P( где P(А)=1-P( т.е. при таком способе проверки мы обнаружим брак в 45% случаев. б) Чтобы наступило событие P( Итак, P(А)=1-P( т.е. при таком способе проверки мы обнаружим брак в 87% случаев. Ответ: а) 0,447; б) 0,871.
Задача 10. На следующий год в местности Х прогнозируют две вспышки гриппа. Причем в весенней вспышке заболевают 5%, а в осенне-зимней – 10% людей данной возрастной группы. Считая, что эти вспышки вызываются различными возбудителями (т.е. заболевания в эти периоды независимы) оценить вероятность того, что случайно взятый человек в следующем году переболеет гриппом хотя бы 1 раз. Решение. Обозначим через А событие, состоящее в том, что случайно взятый человек заболеет гриппом весной, через В –осенью, через С – переболеет гриппом хотя бы 1 раз. Тогда С=А+В. По теореме [P(A+B)=P(A)+P(B)-P(AB)] о вероятности суммы двух событий и по теореме [P(AB)= P(A)×P(B)] о вероятности произведения двух независимых событий получим: P(С)=P(A+B)=P(A)+P(B)- P(A)×P(B)= =0,05+0,10-0,05×0,10=0,145, т.е. 14,5% людей переболеют в этом году гриппом хотя бы 1 раз. Ответ: 0,145. Задача 11. Молодожёны планируют, что у них будет 3 дочки и 2 сына. Считая, что у них действительно будет 5 детей найти шанс осуществления их желания, если вероятность рождения девочки 49%. Решение. Обозначим через А событие (успех), состоящее в том, что при данной беременности родится девочка. Тогда супружеская пара проводит 5 независимых «испытаний». Нас интересует событие, состоящее в наступлении ровно трёх успехов, и двух неуспехов. Воспользуемся формулой Бернулли наступления ровно m успехов в серии из n испытаний:
где p вероятность успеха в одном испытании. Итак, вероятность искомого события:
Ответ: вероятность этого события 30%.
Задача 12. Вероятность заболевания гепатитом для жителя некоторой области в определённый период года составляет 5×10-4. Найти вероятность того, что среди 10000 обследованных жителей ровно 5 окажутся заболевшими. Решение. Вероятность успеха в одном испытании очень мала (р =0,0005), а количество испытаний велико (n =10000). Поэтому воспользоваться формулой Бернулли для вычисления вероятности наступления ровно m =5 успехов сложно с точки зрения громоздкости вычислений. Воспользуемся асимптотической формулой Пуассона
Тогда m=0,0005×10000=5. И искомая вероятность равна
Ответ: в 18% таких групп жителей будет ровно по 5 заболевших.
Задание 13. Имеются 3 конверта. В первом конверте 25 контрольных работ по информатике; во втором – 10 контрольных работ по информатике и 5 контрольных работ по математике; в третьем – 15 контрольных работ по математике. Из выбранного наугад конверта вынули контрольную работу по информатике. Найти вероятность того, что контрольная работа взята из первого конверта (событие A). Решение. Из условия задачи, имеем:
Соответственно вероятность выбора контрольных работ из первого, второго, третьего конвертов равна: Тогда вероятность выбора контрольных работ из первого конверта равна:
Ответ: вероятность выбора контрольной работы из первого конверта, равна 0,6. Задание 14. У 10 человек продолжительность инкубационного периода вирусного гепатита составила: 16, 20, 21, 15, 33, 39, 24, 24, 33, 39. Требуется составить статистическое распределение и определить: – математическое ожидание, –дисперсию, –среднеквадратическое отклонение. Решение. Составим статистическое распределение:
1. Найдем математическое ожидание по формуле:
2. Найдем дисперсию СВ по формуле:
Задание 15. Налоговый инспектор, изучая зависимость выработки
Полагая, что между признаками Решение. Для вычисления параметров а и b составим расчетную таблицу:
Составляем систему:
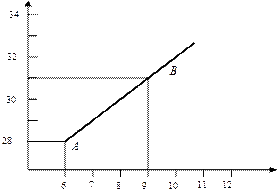
Уравнение регрессии У на Х имеет вид: Построим диаграмму рассеяния и линию регрессии:
Точки
Найдем коэффициент корреляции по формуле:
Зная уравнение регрессии, можно вычислить предполагаемую выработки на одного работника при величине товарооборота магазина 35 ус. ед.
Ответ: при величине товарооборота магазина 35 ус. ед. выработки на одного работника составит 56 ус. ед.
Дата добавления: 2015-12-15 | Просмотры: 952 | Нарушение авторских прав |
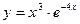 .
. , так как при любом значении
, так как при любом значении  функция имеет определенное вещественное значение. Точек разрыва нет, поэтому интервал непрерывности совпадает с областью определения функции
функция имеет определенное вещественное значение. Точек разрыва нет, поэтому интервал непрерывности совпадает с областью определения функции  .
. ,
,  ;
; ,
,  ,
, 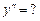
 , тогда
, тогда .
. , где
, где  – константа. Получим:
– константа. Получим: .
. . Тогда
. Тогда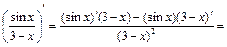
 .
.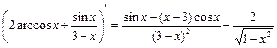 .
. является сложной функцией
является сложной функцией  , где
, где  , применим правило дифференцирования сложной функции
, применим правило дифференцирования сложной функции  . Получим:
. Получим: .
. .
. . Так как
. Так как  , то
, то  . Применим формулу для вычисления производной произведения:
. Применим формулу для вычисления производной произведения:  , полагая
, полагая  , а
, а 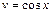 . Таким образом
. Таким образом  . Как и выше, заметим, что
. Как и выше, заметим, что 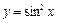 – сложная функция
– сложная функция  , где
, где  , а так как
, а так как  , имеем:
, имеем: .
. .
. .
. 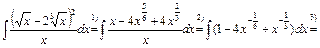
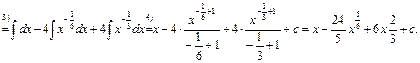 .
. .
. .
. .
. . В прямых скобках показано, почему делается именно такая замена. В остальных строках приведены вспомогательные выкладки.
. В прямых скобках показано, почему делается именно такая замена. В остальных строках приведены вспомогательные выкладки. .
. .
. .
.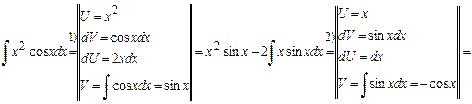
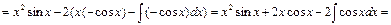

 , используя метод замены переменно
, используя метод замены переменно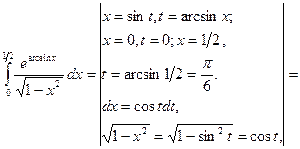
 .
. .
. .
. является парабола, ветви которой направлены вверх, так как
является парабола, ветви которой направлены вверх, так как  , а вершина находится в точке
, а вершина находится в точке  , где
, где ;
;  .
. .
. :
: ;
;  ;
; ;
; .
. и
и  .
. , достаточно указать координаты двух её точек:
, достаточно указать координаты двух её точек: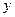
 и
и  .Площадь заштрихованной фигуры
.Площадь заштрихованной фигуры  найдём по формуле
найдём по формуле ,
,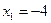 ,
,  ,
,  ,
, 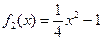 ,
,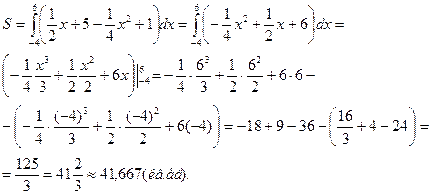
 кв. ед.
кв. ед. фигуры, ограниченной линиями:
фигуры, ограниченной линиями:  ,
,  .
.
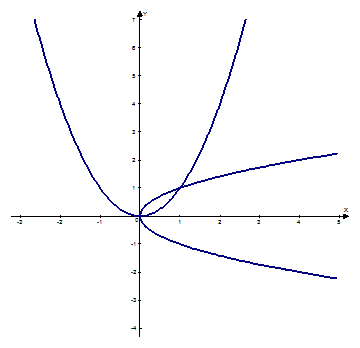
 , определяется по формуле:
, определяется по формуле: ,
,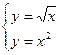
 и
и  .
.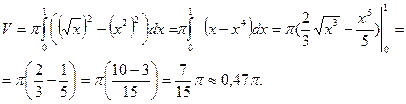
 куб. ед.
куб. ед.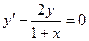

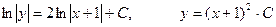
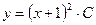
 = 8*(8–1)*(8–2) = 8*7*6 =336.
= 8*(8–1)*(8–2) = 8*7*6 =336. – ни одна из коробок не содержит брак.
– ни одна из коробок не содержит брак. ,
,  , т.е.
, т.е.  =0,553,
=0,553, – вероятность того, что в первой коробке не будет брака;
– вероятность того, что в первой коробке не будет брака;  – того, что во второй тоже не будет брака при условии, что в первой его не было. Итак
– того, что во второй тоже не будет брака при условии, что в первой его не было. Итак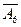 т.е.
т.е.  )= =
)= =  ×
×  ×
×  ×
× 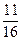 =0,129.
=0,129.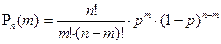 ,
, =
= 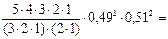 0,30601
0,30601 , где m= p×n.
, где m= p×n. 0,17547
0,17547 – событие, выбор первого конверта;
– событие, выбор первого конверта;  – событие, выбор второго конверта;
– событие, выбор второго конверта;  – событие, выбор третьего конверта.Так как выбор каждого конверта равновероятен, то имеем:
– событие, выбор третьего конверта.Так как выбор каждого конверта равновероятен, то имеем: .
.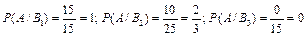 .
.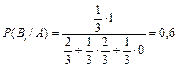
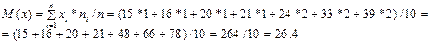
 3. Найдем среднеквадратическое отклонение СВ по формуле:
3. Найдем среднеквадратическое отклонение СВ по формуле: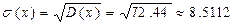
 (ус.ед.) на одного работника от величины товарооборота магазина
(ус.ед.) на одного работника от величины товарооборота магазина  (ус.ед.) за отчётный период обследовал десять магазинов и получил следующие данные.
(ус.ед.) за отчётный период обследовал десять магазинов и получил следующие данные.

 и
и  имеет место линейная корреляционная связь, определить выборочное уравнение линейной корреляции. Построить диаграмму рассеяния и линию регрессии. Сделать вывод о направлении и тесноте связи между
имеет место линейная корреляционная связь, определить выборочное уравнение линейной корреляции. Построить диаграмму рассеяния и линию регрессии. Сделать вывод о направлении и тесноте связи между  (ус. ед.)
(ус. ед.)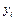





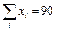
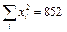



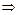


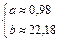
 .
.
 и
и  находим из уравнения регрессии.
находим из уравнения регрессии.
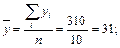


 ,
, .
. .
. корреляция положительная, то есть с возрастанием Х возрастает и У. Теснота связи достаточно большая, так как 0,93
корреляция положительная, то есть с возрастанием Х возрастает и У. Теснота связи достаточно большая, так как 0,93  1.
1. (ус. ед.).
(ус. ед.).