 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
III. Теория вероятностей и математическаяСТАТИСТИКА 3.1. Элементы комбинаторики. Перестановки. Размещения. Сочетания. Бином Ньютона. 3.2. Основы теории вероятностей. Классификация событий. Случайные события. Теоремы сложения и умножения вероятностей. Независимость случайных событий. Формула полной вероятности. Формулы Байеса. Случайные величины: дискретные и непрерывные. Закон распределения дискретной случайной величины. Математическое ожидание, дисперсия, их свойства. Биномиальное распределение. 3.3. Элементы математической статистики. Случайная выборка и закон ее распределения. Эмпирическая функция распределения. Оценки параметров функции распределения по выборке. Надежность. Доверительный интервал. Понятие корреляционной зависимости. Приложения элементов математической статистики к решению задач с биологическим, физическим и химическим содержаниями.
КОНТРОЛЬНЫЕ ЗАДАНИЯ Задание 1. Найти область определения функции В1. В5. В9. В13. В17. В21.
В25. В28. В31. В34. В38.
Задание 2. Построить по шагам график функции, используя правила преобразования графиков В1 В3 В5 В7 В9 В11 В13 В15 В17 В19 В21 В23 В25 В27 В29 В31 В33 В35 В37 В39
Задание 3. Для заданных функций найти первую производную В1. а) В 2. а) В 3. а) В 4. а) В 5. а) В 6. а) В 7. а) В 8. а) В 9. а) В 10. а) В 11. а) В 12. а) В 13. а) В 14. а) В 15. а) В 16. а) В 17. а) В 18. а) В 19. а) В 20. а) В 21. а) В 22. а) В 23. а) В 24. а) В 25. а) В 26. а) В 27. а) В 28. а) В 29. а) В 30. а) В 31. а) В 32. а) В 33. а) В 34. а) В 35. а) В 36. а) В 37. а) В 38. а) В 39. а) В 40. а) Задание 4. Найти неопределенные интегралы:
В12 а) В13 а) В14 а) В15 а) В16 a) В17 a) В18 а) В19 а) В20 а) В21 а)
В25 а) В26 а) В27 a) В28 a) В29 а) В30 а) В31 а) В32 а) В33 а) В34 а) В35 а) В36 a) В37 a) В38 а) В39 а) В40 а) Задание 5. Вычислить определенные интегралы: В1 а) В2 а) В3 a) В4 a) В5 а) В6 а) В7 а) В8 а) В9 а) В10 а) В11 а) В12 а) В13 а) В14 а) В15 а) В16 а) В17 а) В18 а) В19 а) В20 а) В21 а) В22 а) В23 a) В24 a) В25 а) В26 а) В27 а) В28 а) В29 а) В30 а) В31 а) В32 а) В33 а) В34 а) В35 а) В36 а) В37 а) В38 а) В39 а) В 40 а)
Задание 6. а) Вычислить площадь фигуры, ограниченной линиями:
В 1 В 3. В 5. В 7. В 9. В 11. В 13. В 15. В17 В 19 В 21. В 23. В 25. В27 В29.
В 31. В 33. В 35. В 37 В 39
б) Вычислить объем тела, образованного:
вращением вокруг оси В 1 В 2 В 3. В 4. В 5. В 6. В 7. В 8. В 9. В 10.
вращением вокруг оси В 11. В 12. В 13. В 14. В 15. В 16 В 17. В 18. В 19. В 20.
вращением вокруг оси В 21. В 22. В 23. В 24. В 25. В 26. В 27. В 28. В 29. В 30.
вращением вокруг оси В 31. В 32. В 33. В 34. В 35. В 36. В 37. В 38. В 39. В 40. Задание 7.
Найти общее в частное решение дифференциальных уравнений первого порядка. В 1. 2yу' = 3х3 В 2. 2хyy¢=3х5y2, у(1)=-1 В 3.y¢sinx=ycosx,y( В 4. xy' = -x2y2, y(1)=1 В 5. у¢ =ycosx, y( В 6.y¢y= В 7. 2yy¢ tg 2x = sin 2x, y(0) = 0 В 8. В 9. (1 + x2) y¢ у = arctg x, y(0)= 1 В 10.y'cos2xy=tg x, y(0)= -1 В 11. 3x2 dy + 2xydx = 0, y(0) = 1 В1 2. ху¢ arctg y= x, y(l) =0 В1 3. ху¢ В1 4. y¢ = 3x2y, y(0)= 1 В1 5.(1+ex)yy¢=e В1 6.у¢ В1 7. В1 8. (2 –x2) dy = В1 9. В2 0.tgx =yy¢, y(-l)= В 21. у'ху = 3х В 22.хy¢у=3х5 у(1)=-1 В2 3.y¢siny=l,y( В2 4. xy' = -x2y2, y(1)=1 В2 5. yу¢ =cosx, y( В2 6.y¢y= В2 7. y¢ 2y tg 2x = sin 2x, y(0) = 0 В2 8. В2 9. (1 + x2) y¢ у = arctg x, y(0)= 1 В 30.y'cosx=tg x, y(0)= -1 В 31. 3x2 dy + 2xydx = 0, y(0) = 1 В3 2. (ху¢) arctg y= x, y(l) =0 В3 3. ху¢ В3 4. y¢ = 3x2y, y(0)= 1 В3 5.(1+ex)yy¢=ey, y(0)==0 В3 6.у¢ В3 7. y'cos2x=tg x, y(0)= -1
В3 8. (2 –x2) dy = В3 9. В4 0.tg2y =y¢, y(-l)= Задание 8. В1. На городскую конференцию выбирают 5 лучших врачей из 8. Сколькими способами это можно сделать? B2. Замок сейфа открывается, если набрана правильная комбинация из 4 цифр от 0 до 9. Преступник пытается открыть сейф и набирает шифр наудачу. Найдите наибольшее возможное число безуспешных попыток, если все цифры шифра разные. B3. В терапевтическом отделении 20 человек госпитализированы с диагнозом – пневмония и 15 – с диагнозом бронхит. Сколькими способами можно выбрать 3 пациентов на обследование? B4. Сколькими способами можно разложить 5 упаковок аспирина в 5 шкафчиках? B5. На приёме у терапевта 18 человек, в день терапевт осматривает 15 человек. Сколькими способами можно составить очередь к врачу? B6. В группе 30 студентов. Сколькими способами можно выбрать шесть делегатов для переговоров с администрацией института по вопросу о свободной продаже пива в студенческом буфете? B7. Сколькими способами можно выбрать 4 из 20 больных на уколы? B8. В полуфинале первенства по шахматам участвует 20 студентов, а в финал выходят лишь трое. Сколько различных комбинаций по три студента можно получить в данном случае? B9. Имеется 8 штаммов бактерий, для определения скорости их роста необходимо выбрать 4. Сколькими способами это можно сделать? B10. Сколькими способами можно сделать больному инъекцию от трёх разных болезней, если имеются 3 шприца с различной вакциной? B11. Сколькими способами можно разместить 4 скальпеля разной величины на хирургическом столе? B12. Сколько слов можно составить их букв в слове “ПУЛЬМАНОЛОГ”? B13. Сколькими способами можно выбрать 3-ёх медсестёр и одного санитара из группы, состоящей из 8 медсестёр и 3–ёх санитаров? Дата добавления: 2015-12-15 | Просмотры: 1248 | Нарушение авторских прав |
 В2.
В2. 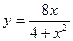 В3.
В3. 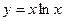 В4.
В4. 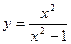
 В6.
В6.  В7.
В7.  В8.
В8. 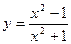
 В10.
В10.  В11
В11  В12.
В12. 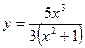
 В14.
В14.  В15.
В15.  В16.
В16. 
 В18.
В18.  В19.
В19.  В20.
В20. 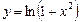
 В22.
В22. 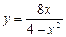 В23.
В23.  В24.
В24. 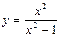
 В26.
В26.  В 27.
В 27. 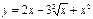
 В29.
В29.  В30.
В30. 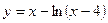
 В32.
В32.  В33.
В33. 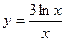
 В35.
В35. 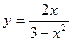 В36.
В36.  В37.
В37. 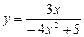
 В39.
В39.  В40.
В40. 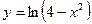
 В2
В2 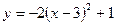
 В4
В4 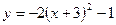
 В6
В6 
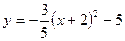 В8
В8 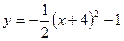
 В10
В10 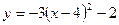
 В12
В12 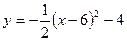
 В14
В14 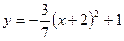
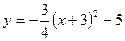 В16
В16 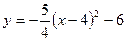
 В18
В18 
 В20
В20 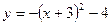
 В22
В22 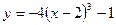
 В24
В24 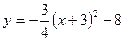
 В26
В26 
 В28
В28 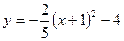
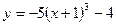
 В32
В32 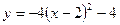
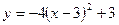 В34
В34 
 В36
В36 
 В38
В38 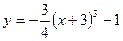
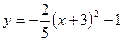
 ;
; ; б)
; б) 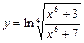 ; в)
; в)  .
. ; б)
; б)  ; в)
; в) 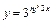
 ; б)
; б)  ; в)
; в) 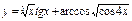
 ; б)
; б) 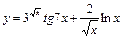 ; в)
; в) 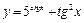
 ; б)
; б)  ; в)
; в) 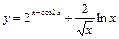
 ; б)
; б)  ; в)
; в) 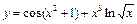
 ; б)
; б)  ; в)
; в) 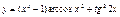
 ; б)
; б)  ; в)
; в) 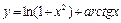
 ; б)
; б)  ; в)
; в) 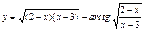
 ; б)
; б)  ; в)
; в) 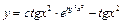
 ; б)
; б)  ; в)
; в) 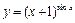
 ; б)
; б)  ; в)
; в) 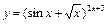
 ; б)
; б)  ; в)
; в) 
 ; б)
; б)  ; в)
; в) 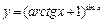
 ; б)
; б) 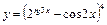 ; в)
; в) 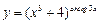
 ; б)
; б)  ; в)
; в) 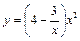
 ; б)
; б)  ; в)
; в) 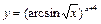
 ; б)
; б)  ; в)
; в) 
 ; б)
; б)  ; в)
; в) 
 ; б)
; б)  ; в)
; в) 
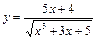 ; б)
; б)  ; в)
; в) 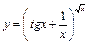
 ; б)
; б)  ; в)
; в) 
 ; б)
; б)  ; в)
; в) 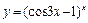
 ; б)
; б)  ; в)
; в) 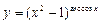
 ; б)
; б)  ; в)
; в) 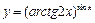
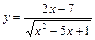 ; б)
; б)  ; в
; в 
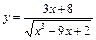 ; б)
; б)  ; в)
; в) 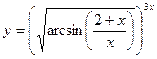
 ; б)
; б)  ; в)
; в)  ; в)
; в) 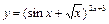
 ; в)
; в) 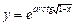
 ; б)
; б)  ; в)
; в) 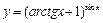
 ; б)
; б)  ; в)
; в) 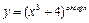
 ; в)
; в) 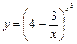
 ; б)
; б)  ; в)
; в)  ; б)
; б)  ; в)
; в) 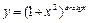
 ; в)
; в)  ; в)
; в)  ; в)
; в)  .
.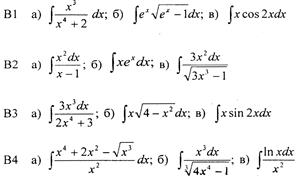
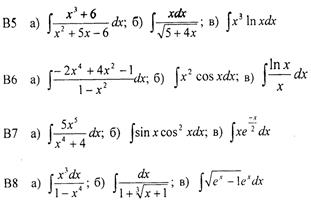
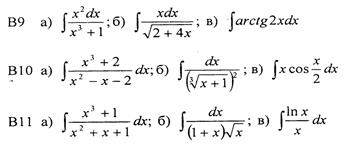
 б)
б)  ; в)
; в) 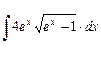
 б)
б)  ; в)
; в) 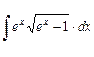

 б)
б)  в)
в) 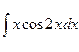
 б)
б)  в)
в) 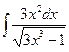
 б)
б) 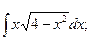 в)
в) 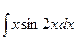
 б)
б)  в)
в) 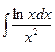
 б)
б) 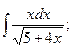 в)
в) 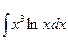
 б)
б)  в)
в) 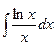
 б)
б) 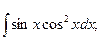 в)
в) 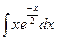
 б)
б)  в)
в) 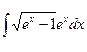


 в)
в) 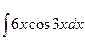
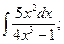 б)
б)  в)
в) 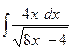
 б)
б)  в)
в) 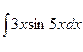
 б)
б)  в)
в) 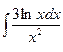
 б)
б)  в)
в) 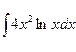
 б)
б)  в)
в) 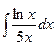
 б)
б)  в)
в) 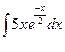
 б)
б) 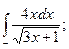 в)
в) 
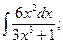 б)
б)  в)
в) 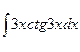
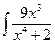
 в)
в)  б)
б)  в)
в)  б)
б)  в)
в) 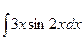
 в)
в)  б)
б)  в)
в) 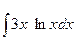
 б)
б)  в)
в) 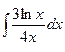
 б)
б)  в)
в) 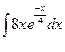
 б)
б) 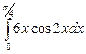
 б)
б) 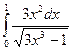
 б)
б) 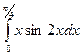
 б)
б) 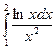
 б)
б) 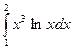
 б)
б) 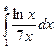
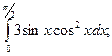 б)
б) 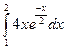
 б)
б) 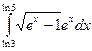
 б)
б) 
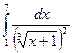 ; б)
; б) 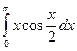
 б)
б) 
 б)
б) 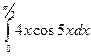
 б)
б) 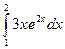
 б)
б) 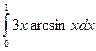
 б)
б) 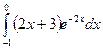
 б)
б) 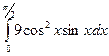
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 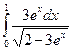
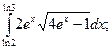 б)
б) 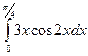
 б)
б) 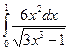

 б)
б) 
 б)
б) 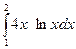
 б)
б) 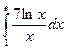
 б)
б) 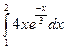
 б)
б) 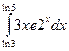
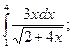 б)
б) 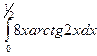
 ; б)
; б) 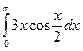
 б)
б) 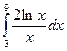
 б)
б) 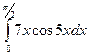
 б)
б) 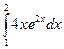
 б)
б) 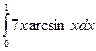
 б)
б) 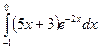
 б)
б) 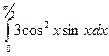
 б)
б) 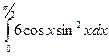
 б)
б) 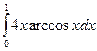
 б)
б) 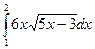
 б)
б)  ;
;  . В 2.
. В 2.  ;
; 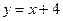 .
.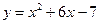 ;
;  . В4.
. В4.  ;
;  .
. . В 6.
. В 6.  ;
;  .
.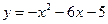 ;
;  ;
; 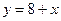 .
. ;
;  . В10.
. В10.  ;
;  ;
; 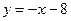 . В 12
. В 12  ;
;  .
. ;
;  . В14
. В14  ;
;  .
. ;
; 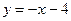 . В 16.
. В 16.  ;
;  ;
;  ;
;  . В 20.
. В 20.  ;
;  .
.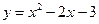 ;
;  . В24
. В24 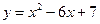 ;
;  . В 26.
. В 26.  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  ;
;  .
.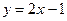 . В 34.
. В 34.  .
. ;
;  ;
;  .
.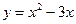 ;
;  . В 38.
. В 38. 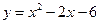 ;
; 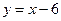 .
. ;
;  . В40
. В40  ;
;  .
.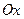 фигуры, ограниченной линиями:
фигуры, ограниченной линиями: ;
; 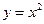 .
. ;
;  .
. ;
;  (одна полуволна),
(одна полуволна), 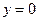 .
. ;
;  ;
;  ;
;  ;
; 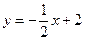 .
. ;
;  ;
;  .
. ;
; 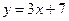 .
. (одна полуволна);
(одна полуволна);  ;
;  .
. фигуры, ограниченной линиями:
фигуры, ограниченной линиями: ;
;  .
. ;
; 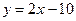 ;
;  .
. ;
;  ;
; 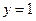 .
. ;
;  .
. ;
;  ;
;  ;
; 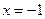 .
. ;
; 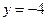 ;
;  (одна полуволна);
(одна полуволна);  .
. ;
;  .
.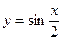 (одна полуволна);
(одна полуволна);  ;
;  .
. ;
;  ;
;  .
. ;
;  .
. ;
;  ;
;  ;
;  .
. ;
;  .
. ;
;  ;
;  , у(0)=0
, у(0)=0 )=0
)=0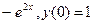
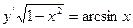 , у(0)= -1
, у(0)= -1 =х, у(1)=0
=х, у(1)=0 , y(0)==0
, y(0)==0 =1+x, у(0)=1
=1+x, у(0)=1 =tgx, у(0)=-1
=tgx, у(0)=-1 dx, y(3) = 1
dx, y(3) = 1 у¢=1, у(1)=1
у¢=1, у(1)=1 , у(0)=0
, у(0)=0 , у(0)= -1
, у(0)= -1 =x, у(0)=1
=x, у(0)=1