 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Необходимая численность выборкиРазрабатывая программу выборочного наблюдения, задаются конкретным значением предельной ошибки и уровнем вероятности. Неизвестной остается минимальная численность выборки, обеспечивающая заданную точность. Ее можно получить из формул средней и предельной ошибок в зависимости от типа выборки. Так, подставляя формулы сначала (39) и затем (40) в формулу (41) и решая ее относительно численности выборки, получим следующие формулы: для повторной выборки n = Вариация ( 1) берется из предыдущих выборочных наблюдений; 2) по правилу «трех сигм», согласно которому в размахе вариации укладывается примерно 6 стандартных отклонений 3) если приблизительно известна средняя величина изучаемого признака, то 4) если неизвестна дисперсия доли единиц, обладающих каким-либо значением признака, то используется ее максимально возможная величина Дата добавления: 2016-06-06 | Просмотры: 647 | Нарушение авторских прав |
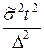 ; (46) для бесповторной выборки n =
; (46) для бесповторной выборки n =  . (47)
. (47)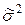 ) значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее берут приближенно одним из способов:
) значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее берут приближенно одним из способов: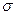 (H/
(H/  2 /9;
2 /9;