 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Методы выявления и оценки корреляционной связиДля выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд методов. 1. Рассмотрение параллельных данных (значений x и y в каждой из n единиц). Единицы наблюдения необходимо расположить по возрастанию значений факторного признака х (как в таблице справа) и затем сравнить с ним (визуально) поведение результативного признака у. В нашей задаче в 6 случаях по мере увеличения значений x увеличиваются и значения y, а в 5 случаях этого не происходит, поэтому затруднительно говорить о прямой связи между х и у. 2. Графический метод – это графическое изображение корреляционной зависимости. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Совокупность полученных точек представляет собой корреляционное поле (рис. 7), а соединяя последовательно нанесенные точки отрезками, получают ломаную линию, именуемую эмпирической линией регрессии (рис. 8).
Визуально анализируя график, можно предположить характер зависимости между признаками x и y. В нашей задаче эмпирическая линия регрессии (рис.8) похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной стоимостного внешнеторгового товарооборота и величиной таможенных платежей в федеральный бюджет. 3. Коэффициент корреляции знаков (Фехнера) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонений (
Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то КФ= 1, что характеризует наличие прямой связи. Если все знаки не совпадут, то КФ=– 1(обратная связь). Если же åС=åН, то КФ= 0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до Средние значения факторного и результативного признаков определяем по формуле средней арифметической простой (10):
В двух последних столбцах таблицы 19 приведены знаки отклонений каждого х и у от своей средней величины. Число совпадений знаков – 10, а несовпадений – 2, тогда определяем коэффициент корреляции знаков (Фехнера) по формуле (80): КФ= Таблица 19. Вспомогательная таблица для расчета коэффициента Фехнера
Обычно такое значение показателя тесноты связи характеризует заметную прямую зависимость между x и y, однако, следует иметь в виду, что поскольку КФ зависит только от знаков и не учитывает величину самих отклонений х и у от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление. 4. Линейный коэффициент корреляции – самый популярный измеритель тесноты линейной связи между двумя количественными признаками x и y. Он основан на предположении, что при полной независимости [24] признаков x и у отклонения значений факторного признака от средней ( В отличие от КФ в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t:
Линейный коэффициент корреляции r представляет собой среднюю величину из произведений нормированных отклонений для x и у:
Числитель формулы (82), деленный на n, представляющий собой среднее произведение отклонений значений двух признаков от их средних значений, называется коэффициентом ковариации – это мера совместной вариации факторного x и результативного y признаков:
Недостатком коэффициента ковариации является то, что он не нормирован, в отличие от линейного коэффициента корреляции. Очевидно, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х и у на произведение их средних квадратических отклонений:
Путем несложных математических преобразований[25] можно получить и другие модификации формулы линейного коэффициента корреляции, например:
Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если Таблица 20. Шкала Чэддока
Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у, а в других свидетельствовать о том, что зависимость не линейная. В нашей задаче для расчета r построим вспомогательную таблицу 21. Таблица 21. Вспомогательные расчеты линейного коэффициента корреляции
В нашей задаче: Тогда линейный коэффициент корреляции по формуле (81): r = 11,241/12 = 0,937. Аналогичный результат получаем по формуле (82): r = 1485,066/(12*4,784*27,618) = 0,937 Или по формуле (85): r = (106317,681/12 – 36,602*238,674) / (4,784*27,618) = 0,937, Найденное значение свидетельствует о том, что связь между величиной стоимостного внешнеторгового товарооборота и величиной таможенных платежей в федеральный бюджет очень близка к функциональной (сильная по шкале Чэддока). Проверка коэффициента корреляции на значимость (существенность). Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x и y, на основе которых он рассчитан. Другими словами, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. Для того, чтобы оценить существенность (значимость) самого r и, соответственно, реальность измеряемой связи между х и у, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σr. Оценка существенности (значимости) r основана на сопоставлении значения r с его средней квадратической ошибкой: Существуют некоторые особенности расчета σr в зависимости от числа наблюдений (объема выборки) – n. 1. Если число наблюдений достаточно велико (n >30), то σr рассчитывается по формуле (89):
Обычно, если 2. Если число наблюдений небольшое (n <30), то σr рассчитывается по формуле (90):
а значимость r проверяется на основе t- критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (91) и сопоставляется c tТАБЛ.
Табличное значение tТАБЛ находится по таблице распределения t -критерия Стьюдента (см. Приложение 2) при уровне значимости α=1-β и числе степеней свободы ν=n–2. Если tРАСЧ> tТАБЛ ,то r считается значимым, а связь между х и у – реальной. В противном случае (tРАСЧ< tТАБЛ) считается, что связь между х и у отсутствует, и значение r, отличное от нуля, получено случайно. В нашей задаче число наблюдений небольшое, значит, оценивать существенность (значимость) линейного коэффициента корреляции будем по формулам (90) и (91):
Из приложения 2 видно, что при числе степеней свободы ν = 12 – 2 = 10 (в 10-й строке) и вероятности β = 95% (уровень значимости α =1 – β = 0,05) tтабл= 2,2281, а при вероятности 99% (α =0,01) tтабл= 3,169, значит, tРАСЧ > tТАБЛ, что дает возможность считать линейный коэффициент корреляции r = 0,937 значимым. 5. Подбор уравнения регрессии [26] представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х, не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у со значениями факторного признака х. Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими. Они обычно обозначаются Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей. Для аналитической связи между х и у могут использоваться виды уравнений, приведенные в таблице 15 (при условии замены t на x). Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной), а все остальные — криволинейными зависимостями. Выбрав тип функции (таблица 15), по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов (МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака
Поставив данное условие, легко определить, при каких значениях a0, a1 и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в теме 6 «Статистическое изучение динамики ВЭД», поэтому, воспользуемся формулой (74) для нахождения параметров теоретической линии регрессии, заменив параметр t на x:
Выразив из первого уравнения системы (92) a0, получим[27]:
Подставив (93) во второе уравнение системы (92), затем разделив обе его части на n, получим:
Применяя 3 раза формулу средней арифметической, получим:
Раскрыв скобки и перенеся члены без a1 в правую часть уравнения, выразим a1:
Параметр a1 в уравнении линейной регрессии называется коэффициентом регрессии, который показывает на сколько изменяется значение результативного признака y при изменении факторного признака x на единицу. Исходные данные и расчеты для нашего примера представим в таблице 22. Таблица 22. Вспомогательные расчеты для нахождения уравнения регрессии
По формуле (96): По формуле (93): a0 = 238,674 – 5,407*36,602 = 40,767. Отсюда получаем уравнение регрессии:
Рис. 9. График эмпирической и теоретической линий регрессии Из рисунка 9 видно, что небольшие различия между эмпирической и теоретической линиями регрессии существуют, поэтому необходимо оценить существенность коэффициента регрессии и уравнения связи, для чего определяют среднюю ошибку параметров уравнения регрессии и сравнивают их с этой ошибкой. Расчет ошибок параметров уравнения регрессии основан на использовании остаточной дисперсии, характеризующей расхождение (отклонение) между эмпирическими и теоретическими значениями результативного признака. Для линейного уравнения регрессии (
Значимость параметров проверяется путем сопоставления его значения со средней ошибкой. Обозначим это соотношение как t:
При большом числе наблюдений (n >30) параметр ai считается значимым, если Если выборка малая (n <30), то значимость параметра ai проверяется путем сравнения с табличным значения t -критерия Стьюдента при числе степеней свободы ν = n -2 и заданном уровне значимости α (Приложение 2). Если рассчитанное по формуле (100) значение больше табличного, то параметр считается значимым. В нашем примере по формуле (99): Находим среднюю ошибку параметра a0 по формуле (97): Теперь находим среднюю ошибку параметра a1 по формуле (98): Теперь по формуле (100) для параметра a0: И по той же формуле для параметра a1: Так как выборка малая, то задавшись стандартной значимостью α=0,05 находим в 10-й строке Приложения 2 табличное значение tα =2,23, которое значительно меньше полученных значений 13,3 и 8,46, что свидетельствует о значимости обоих параметров уравнения регрессии. Наряду с проверкой значимости отдельных параметров осуществляется проверка значимости уравнения регрессии в целом или, что то же самое, проверка адекватности модели с помощью критерия Фишера по Приложению 3. Данный метод уже использовался нами для проверки адекватности уравнения тренда в предыдущей теме, поэтому воспользовавшись формулой (76) в нашем примере получим[29]: Сравнивая расчетное значение критерия Фишера Fр = 71,56 с табличным Fт = 4,96, определяемое по Приложению 3 при числе степеней свободы ν1 = k – 1 = 2 –1 = 1 и ν2 = n – k = 12 – 2 = 10 (т.е. 1-й столбец и 10-я строка) и стандартном уровне значимости α=0,05, можно сделать вывод, что уравнение регрессии значимо. 6. Коэффициент эластичности показывает, на сколько процентов изменяется в среднем результативный признак y при изменении факторного признака x на 1%. Он рассчитывается на основе уравнения регрессии:
где Коэффициент эластичности – величина переменная, т.е. изменяется с изменением значений фактора x. Так, для линейной зависимости
Применительно к рассмотренному уравнению регрессии, выражающему зависимость величины таможенных платежей в федеральный бюджет от величины стоимостного внешнеторгового оборота ( Подставляя в данное выражение разные значения x, получаем и разные значения Э. Так, например, при x = 40 коэффициент эластичности Дата добавления: 2016-06-06 | Просмотры: 896 | Нарушение авторских прав |
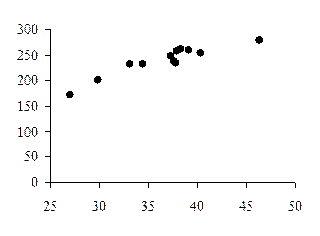
 Рис. 7. Корреляционное поле Рис. 8. Эмпирическая линия регрессии
Рис. 7. Корреляционное поле Рис. 8. Эмпирическая линия регрессии ) и (
) и ( ), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С) и несовпадений (Н). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:
), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С) и несовпадений (Н). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц: . (80)
. (80) 1. Однако, если КФ= 1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у.
1. Однако, если КФ= 1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у.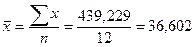 ;
; 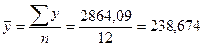 .
.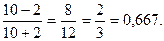

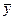
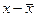 ) носят случайный характер и должны случайно сочетаться с различными отклонениями (
) носят случайный характер и должны случайно сочетаться с различными отклонениями ( ). При наличии значительного перевеса совпадений или несовпадений таких отклонений делается предположение о наличии связи между x и y.
). При наличии значительного перевеса совпадений или несовпадений таких отклонений делается предположение о наличии связи между x и y. и
и 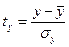 .
. , (81) или
, (81) или  . (82)
. (82)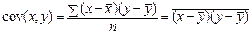 (83)
(83) . (84)
. (84)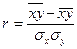 , (85)
, (85) 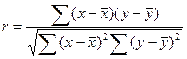 , (86)
, (86) , (87)
, (87) 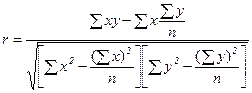 . (88)
. (88) , то r по формуле (85) будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r< 0) – обратную связь. Если
, то r по формуле (85) будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r< 0) – обратную связь. Если  , то r= 0, что означает отсутствие линейной зависимости между х и у, а при r= 1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной. Существует эмпирическое правило (шкала Чэддока) для оценки тесноты связи, представленное в таблице 20.
, то r= 0, что означает отсутствие линейной зависимости между х и у, а при r= 1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной. Существует эмпирическое правило (шкала Чэддока) для оценки тесноты связи, представленное в таблице 20.
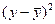

 =
= 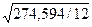 = 4,784;
= 4,784;  =
= 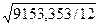 = 27,618.
= 27,618. .
.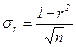 . (89)
. (89) ), где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. Приложение 1).
), где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. Приложение 1). , (90)
, (90) . (91)
. (91)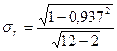 = 0,349/3,162 = 0,110;
= 0,349/3,162 = 0,110;  = 0,937/0,110 = 8,482.
= 0,937/0,110 = 8,482.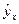 или
или 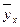 (читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.
(читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.  .
. (92)
(92) . (93)
. (93) . (94)
. (94)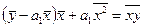 . (95)
. (95) . (96)
. (96)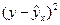

 = 5,407.
= 5,407.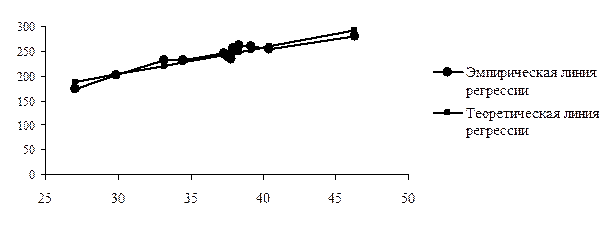
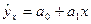 ) средние ошибки параметров a1 и a2 определяются по формулам (97) и (98) соответственно:
) средние ошибки параметров a1 и a2 определяются по формулам (97) и (98) соответственно: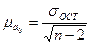 , (97)
, (97)  , (98)
, (98)  . (99)
. (99) , (100)
, (100)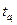 >3.
>3. = 9,669.
= 9,669. = 3,06.
= 3,06. =0,639.
=0,639.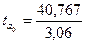 =13,3.
=13,3. =8,46.
=8,46.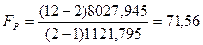
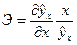 , (101)
, (101) – первая производная уравнения регрессии y по x.
– первая производная уравнения регрессии y по x.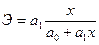 . (102)
. (102) .
.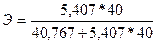 = 0,84, а при x = 50 соответственно
= 0,84, а при x = 50 соответственно  = 0,87 и т.д. Это значит, что при увеличении внешнеторгового товарооборота x с 40 до 40,4 млрд.долл. (т.е. на 1%), величина таможенных платежей возрастет в среднем на 0,84% прежнего уровня; при увеличении x с 50 до 50,5 млрд.долл. (т.е. на 1%) y возрастет на 0,87% и т.д.
= 0,87 и т.д. Это значит, что при увеличении внешнеторгового товарооборота x с 40 до 40,4 млрд.долл. (т.е. на 1%), величина таможенных платежей возрастет в среднем на 0,84% прежнего уровня; при увеличении x с 50 до 50,5 млрд.долл. (т.е. на 1%) y возрастет на 0,87% и т.д.