 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Методические указанияЗадача. На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц (таблица 9): Таблица 9. Результаты бесповторного выборочного наблюдения на предприятии
С вероятностью 0,950 определить: 1) среднемесячный размер дохода работников данного предприятия; 2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.; 3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%. Решение. Для расчета обобщающих характеристик выборки построим вспомогательную таблицу 10. Таблица 10. Вспомогательные расчеты для решения задачи
По формуле (11) рассчитаем средний доход в выборке: Теперь можно определить среднюю ошибку выборки по формуле (40): В нашей задаче
Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в ГС необходимо определить их долю: w = 20/100 = 0,2 или 20%, а затем ее дисперсию по формуле
Доверительный интервал среднего дохода находим по формуле (44): 571-38,494 Аналогично определяем доверительный интервал для доли по формуле (45): 0,2-0,075 В нашей задаче выборка бесповторная, значит, воспользуемся формулой (47), в которую подставим уже рассчитанные дисперсии среднего выборочного дохода рабочих ( nб/повт = Таким образом, необходимо включить в выборку не менее 62 рабочих при определении среднего месячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е., и не менее 197 рабочих при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%. Дата добавления: 2016-06-06 | Просмотры: 712 | Нарушение авторских прав |
 )2
)2
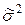 = 4285900/100 = 42859.
= 4285900/100 = 42859. =
=  = 19,640 (у.е.).
= 19,640 (у.е.). = 0,950, значит t = 1,96. Тогда предельная ошибка выборки по формуле (41):
= 0,950, значит t = 1,96. Тогда предельная ошибка выборки по формуле (41): = 1,96*19,64 = 38,494 (у.е.).
= 1,96*19,64 = 38,494 (у.е.). = 0,038 или 3,8%. А затем и предельную ошибку выборки по формуле (41):
= 0,038 или 3,8%. А затем и предельную ошибку выборки по формуле (41):

 = 62 (чел.), nб/повт=
= 62 (чел.), nб/повт=  = 197 (чел.).
= 197 (чел.).