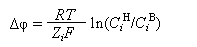Акушерство Анатомия Анестезиология Вакцинопрофилактика Валеология Ветеринария Гигиена Заболевания Иммунология Кардиология Неврология Нефрология Онкология Оториноларингология Офтальмология Паразитология Педиатрия Первая помощь Психиатрия Пульмонология Реанимация Ревматология Стоматология Терапия Токсикология Травматология Урология Фармакология Фармацевтика Физиотерапия Фтизиатрия Хирургия Эндокринология Эпидемиология

Транспорт минеральных веществ в клетку

Прочитайте:

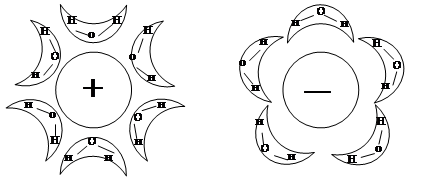
Теперь, когда мы рассмотрели функции минеральных элементов, необходимых для нормального роста растений, следует обсудить механизмы их поступления в растения и структурные элементы, по которым предстоит им двигаться. Минеральные вещества обычно поглощаются из почвы с помощью корней. Они могут поступать в небольших количествах также и через листья, поэтому внекорневое внесение некоторых микроэлементов стало стандартным сельскохозяйственным методом. Минеральные вещества почти всегда поступают в растения в форме ионов. Эти ионы сначала должны пересечь оболочку и плазмалемму, с тем, чтобы попасть в цитоплазму: затем при необходимости пройти и через мембрану, окружающую вакуоль (тонопласт) или какую-либо клеточную органеллу, для того, чтобы оказаться в том или ином внутреннем компартменте.

Изучение вопроса транспорта элементов является одним из основных в проблеме минерального питания. Это предопределяется следующими обстоятельствами. Во-первых, суть питания растений состоит в поступлении и включении в метаболизм минеральных элементов в результате обмена между организмом и средой. Во-вторых, изучение процесса транспорта элементов сопряжено с выяснением свойств и функций клеточной оболочки, мембранных образований, связи между клетками и тканями. В-третьих, выяснение вопросов, связанных с транспортом, приближает нас к целенаправленному управлению продуктивностью сельскохозяйственных растений.

Гидратированное состояние ионов. Перенос ионов через мембрану связан с определенными трудностями. Одной из трудностей является наличие гидратированной воды, которая окружает ион и значительно увеличивает его объем.

Рассмотрим одновалентные ионы, в частности катионы Li⁺, Na⁺, K⁺, Rb⁺ и Cs⁺: самое легкое ядро у лития, а самое тяжелое у цезия. С увеличением массового числа растет также и количество электронов, которые окружают ядро и объем пространства, занимаемого электронными орбиталями. Поскольку плотность электронного облака, окружающего ядро мала, можно предположить, что ядро более доступно внешним воздействиям. Эта зависимость находит свое отражение в величинах радиусов гидратированных ионов: Li⁺ – 0,06; Na⁺ – 0,095; K⁺ – 0,133; Rb⁺ – 0,148; Cs⁺ – 169 нм.

В водных растворах молекулы воды удерживаются около ионов электростатическими силами, источником которых служат заряженные частицы атомного ядра. Чем ближе могут подойти к заряженному атомному ядру молекулы воды, тем сильнее они связываются и тем больше изменяется величина свободной энергии, обусловленная гидратацией. Таким образом, у лития молекулы воды ближе к ядру и это значит, что в гидратной оболочке лития содержится больше молекул воды. Известно, что молекулы воды являются диполями. Около катионов все ближайшие молекулы воды ориентируются отрицательными полюсами внутрь, а около анионов внутрь направлены положительные полюсы молекул воды (рис. 5.1).

Рис. 5.1. Ориентация молекул воды вокруг катиона и аниона

Этот внутренний, сильно связанный с ионами структурированный слой молекул воды, называют первичной оболочкой.

На некотором отдалении, превышающем толщину первичной оболочки, напряженность электрического поля несколько снижается, что приводит к изменению нормальной ориентации молекул воды. Из-за этого вокруг иона возникает вторичная оболочка (рис. 5.2).

Рис. 5.2. Гидратные оболочки иона в водном растворе

Таким образом, благодаря гидратной оболочке размеры ионов сильно увеличиваются. Между радиусами гидратированных и негидратированных катионов щелочных металлов существует обратная зависимость, т. е. гидратированный ион, имеющий меньший кристаллический радиус, имеет большие размеры. Радиусы гидратированных ионов трудно вычислить; данные разных авторов значительно разнятся. Подвижность ионов дает представление об их относительных размерах (табл. 5.2).

Таблица 5.2

Подвижность ионов в водных растворах (25 ^ОС)

Катион	Подвижность, см²·с^-1 · В^-1	Анион	Подвижность, см²·с^-1 · В^-1
К⁺	7,62 · 10^-4	SO₄^2-	8,27 · 10^-4
Na⁺	5,19 · 10^-4	Cl^-	7,91 · 10^-4
Li⁺	4,01 · 10^-4	NO₃^-	7,40 · 10^-4

В настоящее время общепринятыми являются представления о том, что ионы и различные вещества преодолевают мембрану несколькими способами, основные из которых:

1. Простая диффузия через липидную фазу, если вещество растворимо в липидах (это не касается ионов).

2. Облегченная диффузия гидрофильных веществ с помощью липофильных переносчиков (транспортеров).

3. Простая диффузия ионов через гидрофильные поры (например, через ионные каналы).

4. Перенос веществ с участием активных комплексов (насосов).

5. Транспорт веществ путем пиноцитоза в условиях существенных изменений архитектуры мембран.

Что касается движущих сил мембранного транспорта, то различают два механизма.

Пассивный транспорт – перемещение веществ путем диффузии по градиенту электрохимического потенциала без затраты энергии (простая и, в какой-то мере, облегченная диффузия).

Активный транспорт – перемещение веществ против градиента электрохимического потенциала с затратой метаболической энергии, как правило в форме АТФ или редокс-цепей.

Для того чтобы понять механизмы трансмембранного переноса элементов минерального питания, остановимся на рассмотрении некоторых физико-химических закономерностях, определяющих движение ионов в растворе и мембране. Начнем с процессов пассивного транспорта (в частности вспомним законы диффузии).

Согласно первому закону Фика, поток (Ф) прямо пропорционален коэффициенту диффузии D и градиенту концентрации dC/dх в точке х в данный момент времени.

Ф = – D

dх

(5.1)

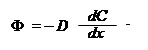Знак минус в правой части уравнения означает, что, если градиент положителен, т. е. концентрация при увеличении х возрастает, диффузионный поток направлен в противоположную сторону.

Однако при описании диффузии на большие расстояния в непрерывной системе уравнения (5.1) необходимо определить зависимость концентрации не только от расстояния, но и от времени. Поэтому целесообразно преобразовать первый закон Фика в дифференциальные уравнения в частных производных, которые обычно называют вторым законом Фика. В одномерном случае этот закон аналитически выражается следующим образом:

(5.2)

= D

d²C

dх²

т. е. скорость изменения концентрации пропорциональна второй производной от концентрации на координате х. Из этого закона мы получаем очень важное соотношение:

(5.3)

х =

Скорость прохождения иона через мембрану в сильной степени зависит от его поведения в самой мембране (липидном бислое). Важными параметрами являются активность и подвижность данного иона в самой мембране. Так как действительный градиент концентрации в мембране неизвестен, то силой, определяющей движение молекул, обычно считают средний градиент:

(5.4)

Если обозначить через S количество вещества, которое входит в клетку, то dS/dt будет характеризовать скорость поступления этого вещества. Поток Ф – это скорость поступления вещества в пересчете на единицу площади, т. е. (1/ А) (dS/dt).

На поверхности мембраны в растворе концентрация веществ может отличаться. Учитывая коэффициент распределения К и все другие высказанные соображения, первый закон Фика можно записать следующим образом:

∆ х

(5.5)

где dS/dt – положительная величина, если вещество поступает в клетку, т. е. если концентрация вещества в среде больше, чем его концентрация в клетке.

В уравнении (5.5) нам неизвестен ни коэффициент распределения, ни коэффициент диффузии, ни действительная величина ∆ х, поэтому эти три параметра было целесообразно заменить одним – коэффициент проницаемости:

∆ х

(см/с)

(5.6)

Коэффициент проницаемости мембраны – это сумма молей вещества, которая прошла через 1 см² мембраны в единицу времени, при условии разности концентраций по обеим сторонам мембраны, составляющей 1 моль/см³.

Коэффициент проницаемости легко определяется из выражения:

(5.7)

Как мы уже отмечали, вещество диффундирует из области высокой концентрации в области низкой концентрации. Движущей силой, такой диффузии служит разность химических потенциалов данного вещества в этих двух областях. Химический потенциал μ_iесть функция концентрации (точнее активности) i-иона:

μ _i = μ _i + RТ ln C_i (5.8)

где μ_i– химический потенциал в стандартных условиях. R – газовая постоянная; Т – абсолютная температура; С_i – концентрация i-иона.

Все это соответствует ситуации переноса вещества в растворе или транспорту через мембрану, когда оно незаряжено. Так как все ионы заряжены, скорость диффузии и распределение в равновесном состоянии определяется не только свойствами мембраны и разницей в концентрациях ионов по обеим сторонам мембраны (химический потенциал), но и разностью электрического потенциала на мембране. Поэтому движение ионов через мембрану обусловлено градиентом электрохимического потенциала.

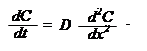
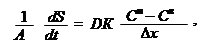
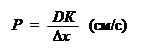
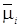Обычно мембрана на внутренней стороне отрицательно заряжена по отношению к наружной поверхности. Это приводит к преимущественному поступлению катионов по сравнению с анионами. В этом случае физической движущей силой будет электрохимический потенциал , в величину которого вносят свой вклад химический и электрический потенциалы:

µ_i

µ_i = µ_i+ RT ln C_i + Z_iFφ,

(5.9)

где – электрохимический потенциал i-иона в стандартных условиях; Z_i – валентность i-иона; F – число Фарадея; φ – электрический потенциал.

Δ µ_i =

µ_i – μ_i

^Н

В реальных условиях описания процесса диффузии ионов в клетку нас интересует разность электрохимических потенциалов (Δφ) по обеим сторонам мембраны, т. е.. Используя уравнение (5.9) можно записать:

(5.10)

µ_i = μ_i

^Н

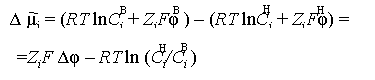
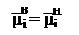В случае равновесного состояния, когда электрохимический потенциал i-иона одинаков по обе стороны мембраны, т. е., получаем:

(5.11)

Разность потенциалов в состоянии равновесия (соотношения) получила название потенциала Нернста.

Чем больше разность потенциалов на мембране, тем сильней обозначена тенденция прохождения катиона по сравнению с анионом. В конечном итоге действие градиента концентрации нейтрализуется градиентом электрического потенциала. Таким образом, мембранный потенциал играет важную роль в прохождении ионов через мембрану.

Важным выводом из приведенных рассуждений является следующий: если даже концентрация i-иона в клетке выше, чем в окружающей среде, это не означает, что на его поступление требуется затрата энергии, процесс может быть и пассивным.

Для многих растительных клеток подавляющая часть пассивного потока ионов складывается главным образом из перемещения трех ионов:K⁺, Na⁺ и Cl^–. При условии электронейтральности: Ф_K+ Ф_Na – Ф_Cl = = 0. Подставив в это соотношение соответствующие выражения для разных Ф_i, можно получить уравнение для диффузионного потенциала (φ_м):

^В

^Н

^В

C _K + α C _Na + γ C _Cl

^Н

^В

^Н

(5.12)

где α = Р _Na/ P _K, γ = P _Cl/ P _K

Уравнение Гольдмана выражает разность электрических потенциалов, возникающих по причине разных тенденций K⁺, Na⁺ и Cl^– диффундировать через мембрану в области более низкого электрохимического потенциала.

Основные допущения, сделанные при выводе уравнения Гольдмана:

– постоянство электрического поля в мембране;

– постоянство коэффициента активности в мембране;

– коэффициент распределения одинаков по обеим сторонам мембраны.

Сравнение величины коэффициентов проницаемости плазмалеммы к ионам K⁺, Na⁺ и Cl^– показывает, что мембрана главным образом проницаема для ионов K⁺:

Рк: Р_Na: Р_Cl = 1,0: 0,2: 0,11 (харовые водоросли);

Рк: Р_Na: Р_Cl = 1,00: 0,68: 0,34 (колеоптили овса);

Рк: Р_Na: Р_Cl = 1,00: 0,04: 0,45 (аксон кальмара).

Дата добавления: 2014-12-11 | Просмотры: 991 | Нарушение авторских прав

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

При использовании материала ссылка на сайт medlec.org обязательна! (0.012 сек.)

Главная | О нас | Полезные cсылки | Контакты