|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Образование остаточных напряжения после пластической деформацииА. Основные механические свойства конструкционных материалов определяются испытанием образцов на растяжение. В процессе таких испытаний устанавливается зависимость между напряжениями растяжении σ и деформацией ε. Типичная кривая деформирования показана на рис.4.1. Первый участок кривой обычно соответствует линейной зависимости, причем
где Е – модуль упругости материала. Далее образуются не только упругие, но и пластические (остаточные) деформации, которые при напряжении, равном пределу текучести материала
Рис.4.1. Кривая деформирования для конструкционных материалов.
Уравнение кривой деформирования можно записать в следующем виде:
где n определяется из условия, что кривая проходит через точку, соответствующую пределу прочности материала Обычно значения n лежат в пределах Для расчетов используются схематизированные кривые деформирования, показанные на рис.4.2.
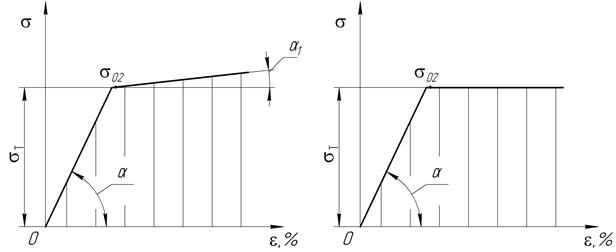
а) б) Рис.4.2. Схематизированные кривые деформирования: а – кривая без упрочнения, б – кривая с линейным упрочнением.
Кривая без упрочнения (рис.4.2. а) пригодна для описания сравнительно небольших пластических деформаций материалов, имеющих площадку текучести (например, для малоуглеродистых сталей). Кривая с линейным упрочнением даст лучшее приближенно действительной кривой деформирования. На втором участке этой кривой
Модуль упрочнения Е' значительно меньше модуля упругости обычно [
Рис.4.3. Кривая деформирования при наличии разгрузки.
Важное свойство процесса деформации состоит в следующей. Если нагрузить образец выше предела текучести (точка А на рис.4.3) и затем снять нагрузку, то разгрузка будет происходить по кривой АВ, близкой к прямой, параллельной начальному участку. Зависимость между изменением напряжения и изменением деформации соответствует материалу, находящемуся в упругом состоянии. Процесс разгрузки можно представить как приложение напряжения
После разгрузки в материале сохранится остаточная деформация
Если снова провести процесс нагружения, то он пойдет по кривой ВАС; новые пластические деформации будут возникать при σ > σ1. Для механизма образования остаточных напряжений существенно поведение материала при последовательной нагружении различных знаков (рис.4.4). Кривая ОАС представляет собой обычную кривую деформирования. В точке А начинается разгрузка (участок АВ), а затем проводится нагружение другого знака (сжатие, участок ВС1). Кривая ВС1 идет несколько выше кривой ВА1С1, повторяющей ветвь ВАС, что объясняется эффектом Баушнигера.
Рис.4.4. Кривая деформирования при изменении направления нагрузки.
Б. В основе определения остаточных напряжений после пластических деформаций лежит известная в теории пластичности теорема о разгрузке..В соответствии с этой теоремой, остаточные напряжения равны разности между истинными напряжениями в упруго-пластическом теле и теми напряжениями, которые создавались бы в нем при предложении об идеальной упругости материала.
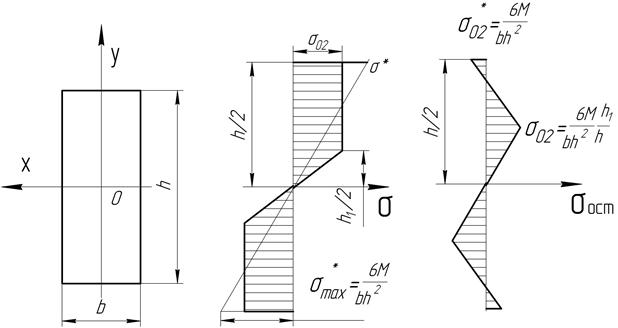
Рис.4.5. Изгиб стержня
Поясним теорему на примере нагиба стержня (рис.4.5) Для расчета принимается схематизированная кривая деформирования без упрочнения (см.рис.4.2.а). Если величина изгибающего момента такова, что наибольшее напряжение изгиба
При условии
в крайних волокнах стержня возникает пластическая деформация.
Пусть при данном значении М область пластической деформации будет от
Эпюра распределения напряжений в стержне показана на рис.4.6.а.
Рис.4.6. Остаточные напряжения после пластического нагиба стержня.
Напряжение определяется следующим равенством:
Если материал стержня был бы идеально упругим, то распределение напряжений соответствовало бы линейному закону
причем наибольшее напряжение
В соответствии с теоремой о разгрузке остаточные напряжения в стержне (после снятия момента М) будут равны
Например, при
При
Эпюра остаточных напряжений приведена на рис.4.6.б. Эта эпюра является самоуравновешенной, т.е. равнодействующие усилия и момент равны нулю. После снятия момента ось стержня будет иметь остаточный прогиб, который также может быть определен по теореме о разгрузке. При действии момента М деформация слоя на расстоянии
где R – радиус кривизны оси стержня. Наибольший прогиб оси стержня
При идеально упругом материале
и наибольший прогиб
Остаточный прогиб
Этот прогиб направлен и сторону прогиба стержня при действии внешнего момента М, так как В. Теорема о разгрузке основана на следующих соображениях. Пусть к телу приложена система внешних сил и в нем возникли упруго-пластические деформации в процессе простого нагружения (напряжения в данной точке возрастают пропорционально одному параметру). Процесс разгрузки можно представить как процесс нагружения усилиями противоположного направления. При этом нагружении (см. рис.4.3 и 4.4) тело ведет себя как упругое. Остаточные напряжения (после двух процессов нагружения - в прямом и обратном направлениях) будут равны разности между напряжениями в yпругo-пластическом теле и упругом теле при одних и тех же нагрузках. Теорема справедлива в том случае, если в процессе разгрузки не наступают повторные пластические деформации (отклонение линии АВС1 от прямой на рис.4.4). Из теоремы о разгрузке вытекает, что эпюра остаточных напряжений (для произвольного сечения) всегда является самоуравновешенной, т.е. равнодействующие: силы и моменты равны нулю. Заметим также, что если распределение напряжений в упруго-пластическом теле и в упругом одинаково (что имеет место в статически определимых системах), то остаточные напряжения после пластической деформации не возникают. В качестве примеров можно Г. Рассмотрим остаточные напряжения после пластического кручения вала (рис.4.7). Если на внешнем радиусе касательное напряжение при кручении
где При кривой деформирования
На рис.4.7.а приведено распределение напряжений
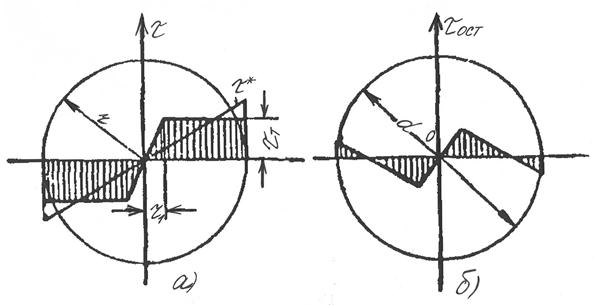
Эпюра остаточных напряжений дана на рис.4.7.а. В дисках турбомашин иногда создают остаточные напряжения с помощью вращения с большой скоростью. На рис.4.8.а, а показано распределение окружных напряжений в диске постоянной толщины с центральным отверстием. Остаточные напряжения представляют собой разность напряжений в упруго-пластическом и упругом телах (см. рис.4.7.б). Д. С физической точки зрения образование остаточных напряжений после пластической деформации связано с необратимыми (остаточными) изменениями объема. Эти изменения объема, остающиеся после снятия нагрузки и вызывают остаточные напряжения.
Рис.4.7. Остаточные напряжения после пластического кручения круглого вала
Например, в диске (рис.4.8.а) при вращении с большой угловой скоростью возле отверстия напряжения превышают предел текучести, и возникает остаточная деформация растяжения. После остановки все частицы диска стремятся вернуться па первоначальные окружности (свойства упругости материала), и в области отверстия возникают сжимающие остаточные напряжения (рис.4.8. б).
Рис.4.8. Окружные остаточные напряжения после пластической деформации диска
Образование остаточных напряжений в результате неоднородной В некоторых процессах (обкатке роликами, обдувке дробью) преднамеренно создается неоднородная пластическая деформация для образования благоприятных остаточных напряжений. Наконец, пластическая деформация возникает при значительных температурных напряжениях в случае интенсивного нагрева или охлаждения деталей.
Дата добавления: 2015-01-18 | Просмотры: 1799 | Нарушение авторских прав |
 , (4.1)
, (4.1) составляют 0,2%.
составляют 0,2%.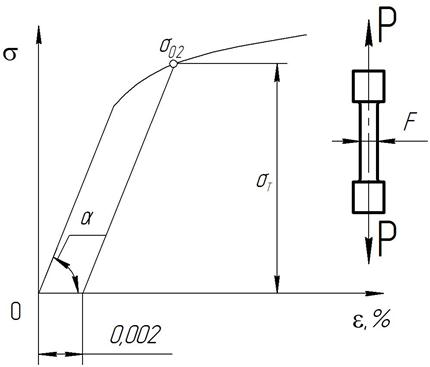
 , (4.2)
, (4.2) .
. .
.
 . 4.3)
. 4.3) ]. Для многих конструктивных материалов (например, для сталей) кривые деформирования при растяжении и сжатии имеют одинаковый вид (в области пластических деформаций ε< 5%).
]. Для многих конструктивных материалов (например, для сталей) кривые деформирования при растяжении и сжатии имеют одинаковый вид (в области пластических деформаций ε< 5%).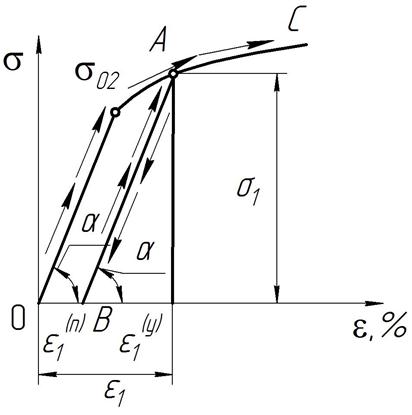
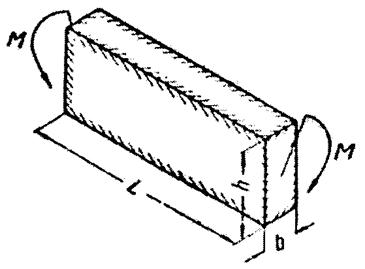
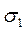 с обратным знаком. Тогда возникшая деформация
с обратным знаком. Тогда возникшая деформация . (4.4)
. (4.4) . (4.5)
. (4.5)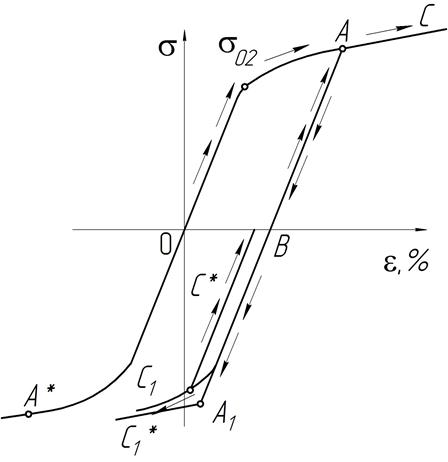
 , то стержень работает в области упругой деформации
, то стержень работает в области упругой деформации (4.6)
(4.6)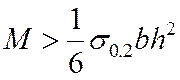
 до
до  (рис.4.6). в этой области
(рис.4.6). в этой области  . При
. При  напряжения изменяются по линейному закону
напряжения изменяются по линейному закону .
.
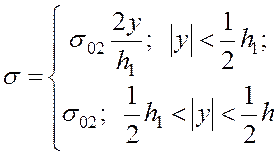 . (4.7)
. (4.7)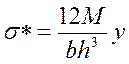 ,
, .
. .
.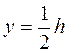
 ;
;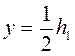
 .
. от оси стержня
от оси стержня ,
,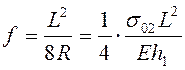
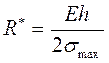
 .
. . (4.8)
. (4.8) .
. ,
, - предел текучести материала при сдвиге, то вал работает в упругой области.
- предел текучести материала при сдвиге, то вал работает в упругой области. без упрочнения (γ – деформация сдвига) распределение напряжений показано на рис.4.7.а. Величина радиуса
без упрочнения (γ – деформация сдвига) распределение напряжений показано на рис.4.7.а. Величина радиуса 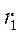 , ограничивающего область упругих деформаций,
, ограничивающего область упругих деформаций,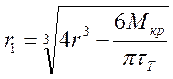 . (4.9)
. (4.9) в идеально упругом материале, соответствующее тому значению крутящего момента. Остаточные напряжения после пластического кручения равны
в идеально упругом материале, соответствующее тому значению крутящего момента. Остаточные напряжения после пластического кручения равны .
.