АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Множественное решение

На рисунках 9 и 17 решение задачи являлось единственным. Крайнее положение линии уровня пересекало ОДП в одной точке, следовательно, и оптимальный план был один.

Однако, если градиент проходит перпендикулярно одной из сторон ОДП, оптимальных планов может быть бесконечно много (в этом случае пересечение крайнего положения линии уровня с ОДП может представлять собой всю эту сторону).

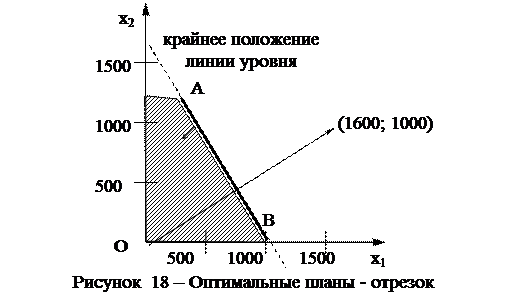
Например, предположим, что в задаче из раздела 1.1 прибыль от карамели составляет не 108 и 140 руб. на тонну, а соответственно 160 и
100 руб. Тогда целевая функция примет вид: mах (160х₁ + 100х₂).

Направление градиента этой функции и крайнее положение линии уровня (пунктир) показаны на рисунке 18. При этом видно, что крайнее положении линии уровня полностью совпадает с прямой, которая соответствует ограничению по запасам сахара. Любая точка, которая лежит на этой прямой и в то же время является допустимым планом, будет давать наиболее высокую прибыль (одну и ту же для всех точек) и, следовательно, будет оптимальным планом. Таких планов будет бесконечное множество, и все они лежат на отрезке АВ. На рисунке 18 множество оптимальных планов выделено более жирной линией.

Чтобы убедиться, что совпадение прямых не является результатом неточного построения графика, а имеет место на самом деле, следует сравнить коэффициенты целевой функции – 160 и 100 – с коэффициентами ограничения по запасам сахара – 0,8 и 0,5. В самом деле,160/0,8 = 100/0,5 =
= 20. Коэффициенты этих прямых пропорциональны, следовательно, сами прямые – линия уровня целевой функции и ограничение по сахару – параллельны (при этом они перпендикулярны градиенту целевой функции).

Найдем координаты оптимальных планов. Координаты точки А были найдены в разделе 2.1: А = (266 2/3; 1173 1/3). В = (1000; 0). Чтобы вывести формулу для любого оптимального плана Х^*, воспользуемся формулой координат отрезка Х^* = k*A + (1 - k)*B = k*(266 2/3; 1173 1/3) + (1 - k)*
*(1000; 0) = (k*266 2/3 + (1 - k)*1000; k*1173 1/3 + (1 - k)*0) = (1000 –
- 733 1/3*k; 1173 1/3*k), где k Î[0; 1].

Подставляя в полученную формулу различные значения k, можно получить различные точки на отрезке АВ. При k = 0 и k = 1 будут получены соответственно концы отрезка B и А. При k = 0,5 будет получена середина отрезка АВ с координатами (1000 – 733 1/3*0,5; 1173 1/3*0,5) = (633 1/3;
586 2/3). При k = 0,1 будет получена точка с координатами (1000 –
- 733 1/3*0,1; 1173 1/3*0,1) = (926 2/3; 117 1/3). Если найти эту последнюю точку на графике, станет видно, что она разбивает отрезок АВ в пропорции 9:1 (находится от точки В на расстоянии, равном ровно одной десятой длины всего отрезка). Таким образом, становится понятен смысл величины k, - она представляет собой ту долю длины отрезка, которая «отсчитывается» от его конца.

Для оптимального плана может быть выведена и другая формула, если взять точку В в качестве начала, а точку А – в качестве конца. Но при подстановке в эту формулу различных значений k все равно будут получены точки на том же самом отрезке.

Итак, чтобы производить карамель оптимальным образом, необходимо выпускать карамель «Снежинка» в количестве 1000 – 733 1/3*k (т), а карамель «Яблочная» - в количестве 1173 1/3*k (т), где k Î[0; 1].

Какую прибыль получит при этом кондитерская фабрика? Обычно для расчета оптимума в целевую функцию подставляют найденный оптимальный план.

Если подставить в целевую функцию этой задачи выведенную формулу отрезка, то в результате приведения подобных членов все слагаемые, содержащие параметр k, взаимно уничтожатся, и будет получено постоянное значение прибыли. Однако, такой способ вычисления оптимума является нерациональным. В самом деле, оптимум у задачи – единственный. Для его вычисления в целевую функцию можно подставить любой оптимальный план, в том числе, планы А или В. Легче подставить план В: 160х₁ + 100х₂ = 160*1000 + 100*0 = 160000*.

Итак, оптимальная прибыль кондитерской фабрики составит
160 тыс. руб.

Таким образом, можно сказать, что множество оптимальных планов задачи линейного программирования, может включать 0, 1 или бесконечное множество точек; любая точка на отрезке между оптимальными планами тоже будет оптимальным планом*.

Дата добавления: 2015-01-18 | Просмотры: 825 | Нарушение авторских прав