 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Пример решения задачи графическим способом с помощью ExcelВ универсальном пакете Excel существует специальная программа «Поиск решения» для решения задач математического программирования, в том числе линейного. Однако использование этой надстройки не дает четкого представления о методе решения задачи. Пользователь, не знакомый с теорией линейного программирования, может неверно интерпретировать полученные с ее помощью результаты. Поэтому, вначале мы будем использовать для решения задач лишь средства самой электронной таблицы, и лишь в разделе 6 рассмотрим обращение к «Поиску».
Итак, решим с помощью Excel задачу из раздела 1.1. Для построения графика (диаграммы) подготовим таблицу 2. В первых строке и столбце таблицы 2 указаны номера соответственно столбцов и строк электронной таблицы Microsoft Excel; при заполнении электронной таблицы их вводить не надо. В строке 1 введены первые координаты точек (х1), по которым будет строиться диаграмма. Вначале их можно задать произвольно, например, 0, 100 и 300. Таких чисел не обязательно должно быть три; существенно, чтобы их было не меньше двух. В столбце А введен текст, из которого будут получены имена рядов в легенде диаграммы. В остальных строках (2-5) введены вторые координаты этих точек (х2). Например, чтобы ввести вторые координаты для точек, по которым будет строиться первое ограничение, следует выразить х2 через х1 из уравнения 0,8х1 + 0,5х2 = 800: х2 = (800 - 0,8х1)/0,5. Следовательно, в ячейку электронной таблицы В2 надо ввести формулу =(800-0,8*B1)/0,5 (поскольку именно в B1 находится значение переменной х1). Аналогично в В3 вводят формулу =(600-0,2*B1)/0,4, а в В4 =(120-0,01*B1)/0,1. В этих ячейках находятся вторые координаты точек, по которым будут строиться второе и третье ограничения. Первая координата, по-прежнему, в В1. Последняя строка предназначена для построения направления градиента. Этот вектор проведем на графике из начала координат. Поэтому для его построения необходимо использовать уравнение прямой, проходящей через начало координат и точку (108; 140). Так как прямая проходит через начало координат, в ее уравнении свободный член равен нулю. Коэффициент этой прямой будет равен 140/108 (= 1 8/27). Таким образом, х2 = х1*140/108. В ячейку В5 введем формулу =B1*140/108. После этого следует выделить диапазон ячеек В2:В5 и скопировать введенные формулы на два столбца справа, т.е. заполнить диапазон С2:D5. При копировании формул изменятся адреса ячеек: в столбце С вместо В1 везде будет стоять адрес С1, а в столбце - D соответственно D1. Таким образом, будут использованы два других значения координаты х1 – 100 и 300. Таблица 2 примет вид:
Таблица 2 – Диапазон для построения диаграммы. Вариант 1
Затем следует выделить весь заполненный диапазон ячеек А1:D5 и обратиться к Мастеру диаграмм. Тип диаграммы выберем Точечная, а вид – со значениями, соединенными отрезками без маркеров. Данные находятся в строках диаграммы. В зависимости от того, как настроена программа, может быть получен разный результат; например, такой, как на рисунке 19. Здесь первый ряд имеет имя «0,8х1 + 0,5х2 <= 800» и построен по точкам, абсциссы которых записаны в первой строке электронной таблицы, а ординаты – во второй (т.е. по точкам (0; 1600), (100; 1440) и (300; 1120)). Второй ряд имеет имя «0,2х1 + 0,4х2 <= 600» и построен по точкам, абсциссы которых те же, а ординаты записаны в третьей строке (т.е. по точкам (0; 1500), (100; 1450) и (300; 1350)). Третий и четвертый ряды построены аналогично (см. таблицу 2).
Полученный вариант диаграммы очевидно является неудачным: хочется продолжить некоторые построенные линии дальше, до их пересечения друг с другом и с горизонтальной осью. Для этого в ячейку D1 вместо числа 300 введем, например, 3000. При этом изменятся все результаты расчетов в столбце D, и диапазон исходных данных для диаграммы примет вид таблицы 3.
Рисунок 19 – Диаграмма. Вариант 1
Таблица 3 – Диапазон для построения диаграммы. Вариант 2
При этом автоматически перестроится построенная диаграмма. Она примет вид, представленный на рисунке 20.
Теперь можно предполагать, что на диаграмме видны все точки пересечения, которые могут понадобиться для решения задачи. Однако, диаграммой по-прежнему неудобно пользоваться. Ее следует отредактировать. Прежде всего, выделим и удалим линии горизонтальной сетки. Затем отформатируем оси. Для этого ось выделяют и в контекстном меню, которое вызывается нажатием правой кнопки мыши, выбирают пункт «Формат оси». В данном случае в «Формате оси» наиболее важной является закладка «Шкала». Форматируя горизонтальную ось, удобно установить минимальное значение на шкале 0, а максимальное – 1500. Для вертикальной оси установим шкалу от 0 до 1600. Значения координат, лежащие за этими границами, при решении задачи не понадобятся. После этого проверим масштаб полученного графика. Это можно сделать разными способами, например, как описано далее. Выделим диаграмму и воспользуемся кнопкой «прямоугольник» на панели «Рисование», удерживая клавишу Shift (последнее делается для того, чтобы получить квадрат). Построим квадрат, левый нижний угол которого будет находиться в начале координат, а длина стороны будет равна, например, 1000 по горизонтальной оси. Результат всех описанных действий представлен на рисунке 21.
Из рисунка 21 видно, что при построении графика нарушен масштаб (1000 т по горизонтали значительно «длиннее», чем по вертикали). Следовательно, диаграмму надо сделать более «узкой» по горизонтали или «широкой» по вертикали. Для этого диаграмму выделяют и подводят курсор мыши к черным отметкам на рамке области диаграммы таким образом, чтобы он принял вид двусторонней стрелки. Затем, удерживая нажатой левую кнопку мыши, изменяют масштаб диаграммы. После такого изменения его снова следует проверить, и так до тех пор, пока масштаб по осям не станет правильным.
Кроме того, нежелательно, чтобы градиент был изображен через всю диаграмму (в этом случае его трудно отличить от ограничений). Чтобы «укоротить» его, удалим в электронной таблице содержимое ячейки D5. Однако, после этого вектор на диаграмме становится слишком «коротким». Чтобы исправить это, введем в C1 вместо 100 число, например, 250. При этом результаты расчетов в столбце С автоматически изменятся, диапазон данных примет вид таблицы 4, а диаграмма будет выглядеть так, как показано на рисунке 22.
Таблица 4 – Диапазон для построения диаграммы. Вариант 3
Рисунок 22 – Диаграмма. Вариант 3
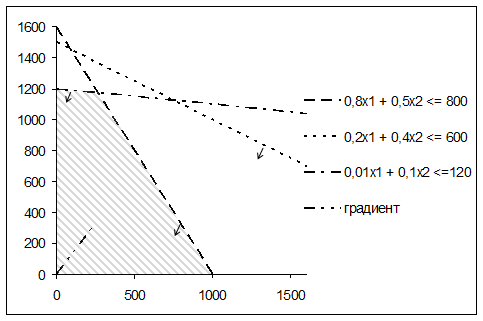
Теперь построенной диаграммой удобно пользоваться. Найдем ОДП задачи, как это было описано в разделе 2.1. Соответствующие рассуждения проиллюстрируем на диаграмме, пользуясь инструментами панели «Рисование». При этом следует помнить, что прежде чем изобразить на диаграмме любой элемент этой панели, следует выделить область диаграммы путем однократного нажатия левой кнопки мыши на белом поле диаграммы. Если не сделать этого до обращения к «Рисованию», то построенный элемент не будет частью диаграммы (при дальнейшем редактировании или перемещении диаграммы он «потеряется» на листе Excel). Для того чтобы обвести ОДП задачи на графике, удобно воспользоваться таким пунктом меню панели «Рисование», как «Автофигуры\Линии\Полилиния». «Полилиния» позволяет изобразить как ломаную линию, состоящую из отрезков, так и любую другую кривую. В первом случае при рисовании линии следует отпускать левую кнопку мыши в каждой вершине ломаной, а во втором – рисовать кривую, не отпуская эту кнопку. Заканчивают рисование незамкнутой ломаной двойным нажатием кнопки мыши. Если ломаная – замкнутая, то рисование будет окончено в тот момент, когда она замкнется. При этом будет предложена автоматическая заливка области внутри этой замкнутой ломаной. Цвет и прозрачность этой заливки можно менять (рекомендуется изменить заливку ОДП на полупрозрачную, чтобы не закрывать другие элементы графика).
В результате диаграмма примет вид, представленный на рисунке 23 (сравните с рисунком 6).
Рисунок 23 – ОДП задачи
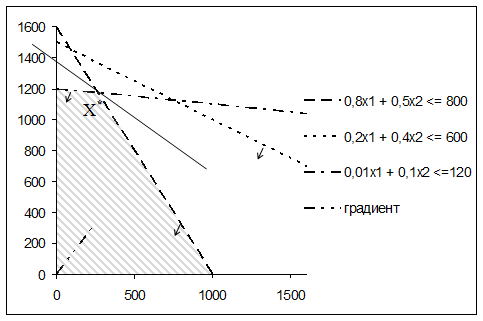
Теперь можно найти оптимальный план Х*. Если сложно представить в воображении положение линии уровня, можно воспользоваться «линией» с панели «Рисование», и в любом месте диаграммы провести перпендикуляр к градиенту. Затем курсор подводят к этой прямой таким образом, чтобы он принял вид крестообразных стрелок и, нажав левую кнопку мыши, перемещают линию уровня в направлении градиента до крайнего положения, как представлено на рисунке 24 (сравните с рисунком 9).
Рисунок 24 – Нахождение оптимального плана
На графике видно, что Х* – точка пересечения прямых, которые соответствуют первому и третьему ограничениям. Следовательно, чтобы найти ее, необходимо решить систему уравнений:
0,01х1 + 0,1х2 =120 Для ее решения удобно воспользоваться надстройкой «Подбор параметра» (см. приложение А). Однако эта надстройка предназначена для решения уравнений, а не систем уравнений. Следовательно, надо преобразовать эту систему в одно уравнение с одной переменной. При построении диаграммы уже использовались формулы, выражающие из этих уравнений х2 через х1.
х2 = (120 – 0,01х1)/0,1, Если вычесть полученные выражения друг из друга, то получим уравнение с одной неизвестной: 0 = (800 – 0,8х1)/0,5 - (120 – 0,01х1)/0,1 Каким образом ввести эту формулу в электронную таблицу? Первое и третье ограничения построены по второй и четвертой строкам электронной таблицы. В диапазоне ячеек В2:D2 и В4:D4 уже находятся формулы для х2. Можно взять любой из этих столбцов и скопировать формулы в любые свободные ячейки. Например, скопируем D2 в Е2, а D4 – в Е4. В результате в Е2 появится формула =(800-0,8*E1)/0,5, а в Е4 =(120-0,01*E1)/0,1. В любую свободную ячейку, например, в Е5 введем разность между этими координатами: =E2-E4. Теперь в ячейке находится формула того уравнения ((800 – 0,8х1)/0,5 - (120 – 0,01х1)/0,1), которое необходимо решить относительно х1. Сама же переменная находится в ячейке E1 (именно на нее ссылаются обе формулы – и в E2, и в E4). Если ячейка Е1 была не заполнена (по умолчанию была нулевой), то столбец Е примет вид, представленный в таблице 5.
Таблица 5 – Подготовка таблицы для использования «Подбора параметра»
Необходимо подобрать в Е1 такое число, чтобы разность в Е5 оказалась равной нулю (результаты вычислений в ячейках E2 и Е4 сравняются). Для этого позиционируем курсор в Е5 и обратимся к «Подбору параметра», указав, что в ней надо установить значение 0, изменяя Е1 (ячейку с переменной х1). После нажатия кнопки ОК в диалоговом окне, представленном на рисунке 25, содержимое столбца Е изменится, как показано в таблице 6.
Рисунок 25 – «Подбор параметра»
Таблица 6 – Результат использования «Подбора параметра»
Таким образом, приближенные оптимальные значения переменных х1 = 266,7 (в ячейке Е1), х2 =1173,3 (в ячейках Е2 и Е4). Если необходимо получить их точные значения в простых дробях, достаточно изменить формат этих ячеек на дробный (при этом решение совпадет с полученным в разделе 2.1). Для получения оптимума достаточно в любую свободную ячейку ввести формулу =108*E1+140*E2 или =108*E1+140*E4. В том и другом случае результат вычислений составит приблизительно 193066,7.
Решение задачи окончено. Его легко можно проверить, построив прямую, которая будет соответствовать крайнему положению линии уровня: 108х1 + 140х2 = 193066,7. Если ввести в таблицу соответствующие формулы и добавить этот ряд в исходные данные диаграммы, то новая прямая должна пройти через точку Х* перпендикулярно градиенту (и пересечь ОДП в этой единственной точке). Вопросы и упражнения 1 Как построить ОДП задачи с двумя переменными, и какой она может быть? 2 Как найти точку оптимума по графику в задаче с двумя переменными? 3 Опишите варианты разрешимости задачи (в геометрической интерпретации). 4 Как подсчитать оптимум в случае множественного решения? 5 Как использовать «Подбор параметра» для решения системы уравнений? 6 Решить с помощью Microsoft Excel следующие задачи:
Указание: пример 1 сводится к задаче с двумя переменными, если выразить х3-5 из уравнений системы ограничений и подставить в целевую функцию. После приведения подобных целевая функция станет функцией двух переменных. В ограничениях можно рассматривать переменные х3-5, как дополнительные (см. раздел 1.4.1), и преобразовать уравнения в неравенства. * Вручную такую прямую можно построить по любым двум точкам. Здесь удобно взять в качестве таких точек корневые, т.е. пересечения этой прямой с осями координат. Для нахождения пересечения с осью ординат возьмем х1 = 0. Тогда 0,8*0 + 0,5х2 = 800; х2 = 800/0,5 = 1600. Для нахождения пересечения с осью абсцисс возьмем х2 = 0. Тогда 0,8х1 + 0,5*0 = 800; х1 = 800/0,8 = 1000. Таким образом, для построения этой прямой можно соединить точки (0; 1600) и (1000; 0). Если строить график по корневым точкам неудобно, можно взять любые другие точки (зафиксировать значение одной переменной равным любому числу и вычислить из уравнения значение другой). * За исключением задач, в которых переменные могут принимать только целые значения: в таких задачах ОДП может включать и более одного, но конечное число допустимых планов. Допустимым планом будет не любая точка на отрезке между допустимыми планами, но только точки с целочисленными координатами. * При подстановке плана А результат будет тот же: 160х1 + 100х2 = 160*266 2/3 + + 100*1173 1/3 = 160000.
* За исключением задач, в которых переменные могут принимать только целые значения: в таких задачах множество оптимальных планов может включать и более одного, но конечное число оптимальных планов. Оптимальным планом будет не любая точка на отрезке между оптимальными планами, но только точки с целочисленными координатами. Дата добавления: 2015-01-18 | Просмотры: 1504 | Нарушение авторских прав |
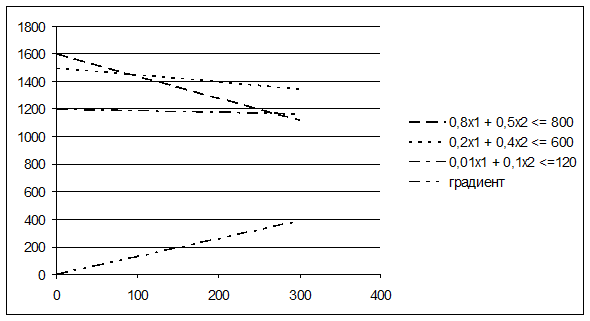
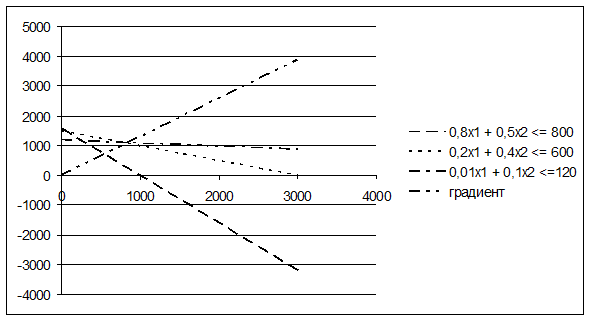 Рисунок 20 – Диаграмма. Вариант 2
Рисунок 20 – Диаграмма. Вариант 2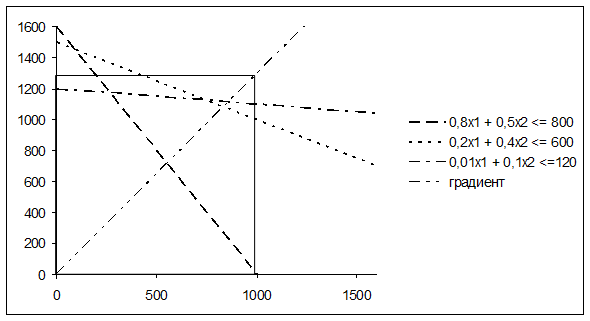 Рисунок 21 – Диаграмма с проверкой масштаба (масштаб неправильный)
Рисунок 21 – Диаграмма с проверкой масштаба (масштаб неправильный)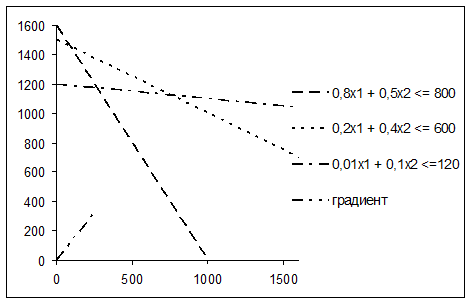
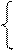 0,8х1 + 0,5х2 = 800
0,8х1 + 0,5х2 = 800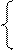 х2 = (800 – 0,8х1)/0,5
х2 = (800 – 0,8х1)/0,5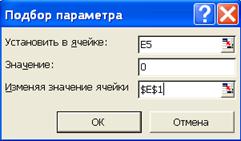
 max -16х1 - х2 + х3 + 5х4 + 5х5
2х1 + х2 + х3 = 10
-2х1 + 3х2 + х4 = 6
2х1 + 4х2 - х5 = 8
х1-5 ³ 0
max -16х1 - х2 + х3 + 5х4 + 5х5
2х1 + х2 + х3 = 10
-2х1 + 3х2 + х4 = 6
2х1 + 4х2 - х5 = 8
х1-5 ³ 0
 max 5х1 + 2х2
10х1 + 4х2 £ 15
2х1 + 5х2 £ 12
х1 + х2 ³ 1
3х1 - х2 £ 10
max 5х1 + 2х2
10х1 + 4х2 £ 15
2х1 + 5х2 £ 12
х1 + х2 ³ 1
3х1 - х2 £ 10
 max х1
х1 - 2х2 £ 0
х1 - х2 ³ -1
х1 + х2 ³ 1
max х1
х1 - 2х2 £ 0
х1 - х2 ³ -1
х1 + х2 ³ 1
 max 3х1 + х2
х2 ³ 6
2х1 + 2х2 £ 3
3х1 - 2х2 ³ 20
max 3х1 + х2
х2 ³ 6
2х1 + 2х2 £ 3
3х1 - 2х2 ³ 20