Случайные величины, случайные элементы
4.1. Пусть (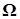 , F) и (R1,B(R1)) - измеримые пространства. , F) и (R1,B(R1)) - измеримые пространства.
Определение. Действительная функция  определенная ( определенная (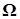 , F), принимающая значения в R1 называется F – измеримой или случайной величиной, если: , F), принимающая значения в R1 называется F – измеримой или случайной величиной, если: 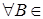 B(R1) B(R1)  F (то есть, прообраз F (то есть, прообраз  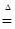  является измеримым множеством в является измеримым множеством в  ). ).
Если  =(Rn,B(Rn)), то B(Rn) – измеримые функции называются борелевскими. =(Rn,B(Rn)), то B(Rn) – измеримые функции называются борелевскими.
Простейшим примером случайной величины является
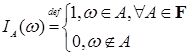
Определение. Случайная величина  представимая в виде представимая в виде
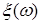  (2) (2)
где     F называется дискретной. Если число слагаемых в сумме в (2) конечно, то случайная величина называется простой. F называется дискретной. Если число слагаемых в сумме в (2) конечно, то случайная величина называется простой.
Замечание. Случайная величина это некоторая характеристика эксперимента, результаты которого зависят от случая  . Требование измеримости важно. Действительно, если на ( . Требование измеримости важно. Действительно, если на (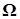 , F) задана вероятностная мера Р и , F) задана вероятностная мера Р и  , то в этом случае можно говорить о вероятности события, состоящего в том, что значение случайной величины принадлежит борелевскому множеству В. , то в этом случае можно говорить о вероятности события, состоящего в том, что значение случайной величины принадлежит борелевскому множеству В.
Определение. Вероятностная мера  на (R,B(R)) с на (R,B(R)) с 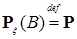  , , 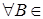 B(R1), называется распределением вероятностей случайной величины B(R1), называется распределением вероятностей случайной величины  на (R, B(R)). на (R, B(R)).
Определение. Функция 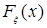  Р Р  , где , где  R1, называется функцией распределения случайной величины R1, называется функцией распределения случайной величины  . .
Замечание. Для дискретной случайной величины мера  сосредоточена не более чем в счетном числе точек и может быть представлена в виде сосредоточена не более чем в счетном числе точек и может быть представлена в виде
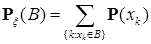 , ,
где  . .
Определение. Случайная величина  называется непрерывной, если ее функция распределения называется непрерывной, если ее функция распределения 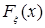 непрерывна. Случайная величина непрерывна. Случайная величина  называется абсолютно непрерывной, если называется абсолютно непрерывной, если  , ,  R1. R1.
4.2. Вопрос: Когда функция  обозначаемая обозначаемая 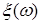 является случайной величиной? Для этого надо проверить условие является случайной величиной? Для этого надо проверить условие  F для любого F для любого 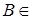 B(R1). B(R1).
Лемма 7. Пусть e – некоторая система множеств такая, что 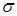 (e)=B(R1). Для того, чтобы (e)=B(R1). Для того, чтобы 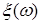 была F - измеримой необходимо и достаточно, чтобы была F - измеримой необходимо и достаточно, чтобы  F для всех F для всех 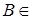 e. e.
Доказательство. Необходимость очевидна.
Достаточность. Пусть D – система борелевских множеств  , для которых , для которых  F. Известно, что: F. Известно, что:
i)  , ii) , ii)  , iii) , iii) 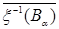 = = 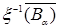 . .
Отсюда следует, что система D – является 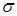 -алгеброй, значит -алгеброй, значит
  D D  B(R1) и B(R1) и 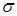 (e) (e)  , следовательно D=B(R1). , следовательно D=B(R1).
Лемма 8. Пусть  : R1 : R1 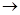 R1 - борелевская функция, а R1 - борелевская функция, а  - случайная величина. Тогда сложная функция - случайная величина. Тогда сложная функция  (то есть (то есть 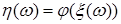 ) - случайная величина. ) - случайная величина.
Доказательство. Действительно
   , ,
так как 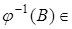 B(R1), B(R1), 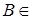 B(R1). B(R1).
Доказательство закончено.
Определение. Функция 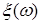 на ( на (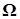 , F) со значениями в , F) со значениями в 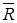 = =  называется расширенной случайной величиной, если: для называется расширенной случайной величиной, если: для 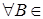 B(R1) B(R1)  F. F.
Теорема 9. 1) Для любой случайной величины  найдется последовательность простых случайных величин найдется последовательность простых случайных величин  таких, что таких, что 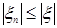 и и  при при  для всех для всех  . .
2) Если случайная величина   , то найдется последовательность простых случайных величин , то найдется последовательность простых случайных величин  таких, что таких, что   для всех для всех  . .
Доказательство. Начнем с пункта 2). Положим  , и , и 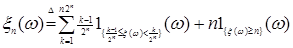
непосредственной проверкой, устанавливается, что  для всех для всех  . Отсюда следует и доказательство пункта 1) так как . Отсюда следует и доказательство пункта 1) так как  можно представить в виде можно представить в виде  , где , где   . .
Теорема 10. Пусть  - последовательность расширенных случайных величин и - последовательность расширенных случайных величин и  = =  . Тогда . Тогда 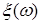 -расширенная случайная величина. -расширенная случайная величина.
4.3. Определение. Пусть  - случайная величина. Пусть множества из - случайная величина. Пусть множества из  вида вида 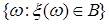 , , 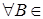 B(R1). Наименьшую B(R1). Наименьшую 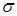 -алгебру порожденную такими множествами называют -алгебру порожденную такими множествами называют 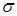 -алгеброй, порожденной случайной величиной -алгеброй, порожденной случайной величиной  и обозначают ее через Fx. и обозначают ее через Fx.
Если  - борелевская функция, то из леммы 7 следует, что - борелевская функция, то из леммы 7 следует, что  - случайная величина, причем Fx - измерима. Оказывается, справедливо и обратное утверждение. - случайная величина, причем Fx - измерима. Оказывается, справедливо и обратное утверждение.
Теорема 11. (Бореля). Пусть  –измеримая случайная величина. Тогда найдется борелевская функция –измеримая случайная величина. Тогда найдется борелевская функция  : R1 : R1 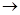 R1 такая, что R1 такая, что  , т.е. для каждого , т.е. для каждого  . (Докажите самостоятельно.) . (Докажите самостоятельно.)
4.4. Определение. Пусть (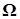 , F) и (E, e) - измеримые пространства. , F) и (E, e) - измеримые пространства. 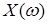 определенная на определенная на 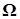 принимающая значения в E называется F / e – измеримой функцией или случайным элементом (со значениями в E принимающая значения в E называется F / e – измеримой функцией или случайным элементом (со значениями в E 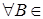 e e  F). (3) F). (3)
Примеры случайных элементов:
1) Если (E, e) = (R1,B(R1)), то определение случайного элемента совпадает с определением случайной величины.
2) Пусть (E, e) = (Rn,B(Rn)). Тогда случайный элемент 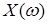 называется n - мерным случайным вектором. Если называется n - мерным случайным вектором. Если  - проекция Rn на - проекция Rn на  -ую координату, то -ую координату, то 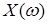 = =  , где , где  . Ясно, что . Ясно, что  - обычные случайные величины. Действительно, для - обычные случайные величины. Действительно, для 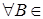 B(R1) B(R1)   R1,.., R1,..,  R1, R1,  R1 R1 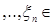 R1 }= R1 }=
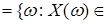 (R1 (R1  R1 R1  R1 R1  R1) R1)  F. F.
Определение. Упорядоченый набор случайных величин  будет называться будет называться 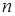 - мерным случайным вектором. - мерным случайным вектором.
В соответствии с этим определением всякий случайный элемент 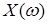 со значениями в Rn будет со значениями в Rn будет 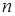 - мерным случайным вектором. Справедливо обратное утверждение: всякий n- мерный случайный вектор - мерным случайным вектором. Справедливо обратное утверждение: всякий n- мерный случайный вектор 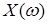 = =  есть случайный элемент в Rn. Действительно, если есть случайный элемент в Rn. Действительно, если 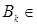 B(R1), B(R1),  , то , то   F, то наименьшая F, то наименьшая 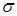 -алгебра, порожденная всеми -алгебра, порожденная всеми  совпадает с B(Rn). поэтому для совпадает с B(Rn). поэтому для 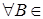 B(Rn) B(Rn)  F. F.
3) Пусть (E, e) = (RТ,B(RТ)), Т – подмножество числовой прямой. В этом случае всякий случайный элемент 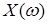 представим в виде представим в виде  с с 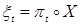 называется случайной функцией с временным интервалом Т. называется случайной функцией с временным интервалом Т.
4.5. Определение. Пусть 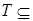 R1. Совокупность R1. Совокупность  называется случайным процессом с временным интервалом Т. Если называется случайным процессом с временным интервалом Т. Если  , то , то  - называется случайным процессом с дискретным временем или случайной последовательностью. Если - называется случайным процессом с дискретным временем или случайной последовательностью. Если 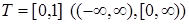 , то , то 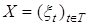 - называется случайным процессом с непрерывным временем. - называется случайным процессом с непрерывным временем.
Определение. Пусть  - случайный процесс. Для каждого - случайный процесс. Для каждого  функция функция  - называется реализацией или траекторией процесса, соответствующего исходу - называется реализацией или траекторией процесса, соответствующего исходу 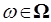 . .
Определение. Пусть  - случайный процесс. Вероятностная мера Р на (RТ,B(RТ)) с P - случайный процесс. Вероятностная мера Р на (RТ,B(RТ)) с P  P P 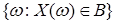 , ,  B(RТ) называется распределением вероятностей процесса Х. B(RТ) называется распределением вероятностей процесса Х.
Определение. Вероятностная мера P  P P  , где , где 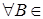 B(Rn), B(Rn),  , называется конечномерными распределениями вероятностей случайного процесса , называется конечномерными распределениями вероятностей случайного процесса  , а n-мерная функция распределения , а n-мерная функция распределения  , где , где  , называется конечномерными функциями распределения процесса , называется конечномерными функциями распределения процесса  . .
4.6. Определение. Пусть (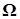 , F, P) - вероятностное пространство и набор ( , F, P) - вероятностное пространство и набор ( e e  ) - измеримых пространств, где ) - измеримых пространств, где  - произвольное множество. Будем говорить, что - произвольное множество. Будем говорить, что  - измеримые функции - измеримые функции  независимы в совокупности, если для любого конечного набора независимы в совокупности, если для любого конечного набора  элементы элементы  - независимы, т.е. для - независимы, т.е. для 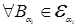 P P  P P  . .
Теорема 12. Для того, чтобы случайные величины  были независимы в совокупности, необходимо и достаточно, чтобы для любого были независимы в совокупности, необходимо и достаточно, чтобы для любого  Rn Rn   , где , где 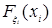  . Докажите самостоятельно. . Докажите самостоятельно.
§ 5. Интеграл Лебега. Математическое ожидание.
5.1. Пусть (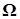 , F, P) - конечное вероятностное пространство, т.е. существует набор множеств , F, P) - конечное вероятностное пространство, т.е. существует набор множеств  таких, что таких, что  при при  и и  , а , а  - простая случайная величина. - простая случайная величина.
Определение. Математическим ожиданием простой случайной величины  , обозначаемым через М , обозначаемым через М  , называется величина M , называется величина M   P (A k). Это определение корректно, так как оно не зависит от способа представления случайной величины P (A k). Это определение корректно, так как оно не зависит от способа представления случайной величины  . Для математического ожидания будем использовать следующее обозначение: . Для математического ожидания будем использовать следующее обозначение:  P P  P. P.
5.2. Дадим определение математического ожидания для случайной величины  . В силу теоремы 9 существует монотонная последовательность простых неотрицательных случайных величин . В силу теоремы 9 существует монотонная последовательность простых неотрицательных случайных величин  таких, что таких, что  при при 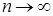 для каждого для каждого  . Очевидно, что M . Очевидно, что M  M M  , поэтому существует , поэтому существует  M M  (причем он может принять значение (причем он может принять значение  ). ).
Определение. Интеграл Лебега относительно вероятностной меры Р случайной величины  , обозначаемый М , обозначаемый М 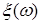 , определяемый равенством M , определяемый равенством M 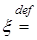  M M  называется математическим ожиданием случайной величины называется математическим ожиданием случайной величины  . .
Это определение будет корректным, если значение предела не зависит от способа выбора аппроксимирующей последовательности  (иначе говоря, если (иначе говоря, если  и и  , то , то  M M  = = 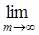 M M  ). ).
Лемма 13. Пусть  - простые неотрицательные случайные величины - простые неотрицательные случайные величины 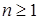 , причем , причем  . Тогда . Тогда  M M  ≥ M ≥ M 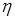 . .
Доказательство. Пусть  и и  . Ясно, что . Ясно, что  и и  , ,
где    , 1B , 1B 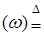  , ,  B B  F. F.
Поэтому
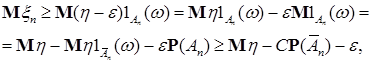
где  . .
Следовательно  . Доказательство закончено. . Доказательство закончено.
Замечание. Из утверждения леммы 13 следует, что 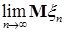  . В силу симметрии имеем . В силу симметрии имеем   . Отсюда вытекает корректность определения. . Отсюда вытекает корректность определения.
5.3. Пусть теперь  - произвольная случайная величина. Обозначим - произвольная случайная величина. Обозначим   . .
Определение. Говорят, что математическое ожидание 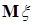 случайной величины случайной величины  существует, если хотя бы одна из величин существует, если хотя бы одна из величин  или или  конечна, т.е. конечна, т.е.  . В этом случае по определению полагается . В этом случае по определению полагается  , а , а 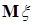 - называется интеграл Лебега от - называется интеграл Лебега от  по мере Р. по мере Р.
Определение. Говорят, что математическое ожидание случайной величины  конечно, если конечно, если  и и  . Отсюда следует, что . Отсюда следует, что  - конечно тогда и только тогда, когда - конечно тогда и только тогда, когда  . .
Наряду с 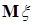 можно рассматривать и можно рассматривать и  , если они определены, то их называют моментами , если они определены, то их называют моментами 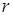 - порядка, где r = 1,2,…,k. - порядка, где r = 1,2,…,k.
5.4. Свойства математического ожидания.
А) Пусть 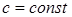 и у случайной величины и у случайной величины 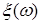 существует существует  , тогда существует , тогда существует  и и  . .
Доказательство. Для простых функций это утверждение очевидно. Пусть  , где , где  - простые случайные величины и - простые случайные величины и  , следовательно , следовательно  . Значит . Значит  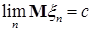 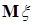 . .
В) Пусть  , тогда , тогда  . .
С) Если существует  , то , то  . .
Доказательство. Так как  , то из А) и В) следует, что , то из А) и В) следует, что  , то есть , то есть  . .
D) Если существует  , то для каждого A , то для каждого A 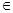 F существует F существует 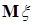  . Если . Если 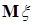 конечно, то конечно, то 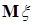  - конечно. - конечно.
Доказательство следует из пункта В), так как  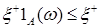 , , 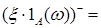  . .
Е) Если  и и 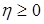 - случайные величины, причем - случайные величины, причем 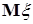  и и  , то , то  . .
Доказательство. Пусть  и и  - последовательность простых функций таких, что - последовательность простых функций таких, что 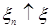 и и  . Тогда . Тогда  и и 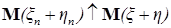 . Кроме того . Кроме того  и и  . Значит . Значит 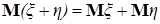 . .
F) Если  , то , то  . .
G) Если  , Р- п.н. и , Р- п.н. и  , то , то  и и 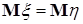 . .
Доказательство. Пусть  , тогда , тогда  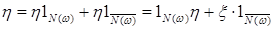 , где , где 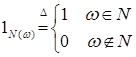 . В силу Е) . В силу Е)  . .
Н) Пусть  и и  , тогда , тогда  Р - п.н. Р - п.н.
Доказательство. Обозначим  . Очевидно, что . Очевидно, что  . .  поэтому в силу свойства В) поэтому в силу свойства В)  , следовательно , следовательно  , значит , значит  для всех для всех 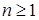 , но , но 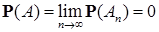 . .
I) Пусть  и и 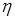 - случайные величины такие, что - случайные величины такие, что  и и  и для всех и для всех 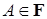   . Тогда . Тогда  Р - п.н.. Р - п.н..
Доказательство. Пусть  . Тогда . Тогда  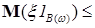  . Поэтому . Поэтому  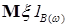 , тогда по свойству Е) , тогда по свойству Е) 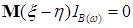 , а в силу Н) , а в силу Н)  P - п.н., значит Р (В)=0. P - п.н., значит Р (В)=0.
J) Пусть  - расширенная случайная величина и - расширенная случайная величина и  , тогда , тогда  P - п.н.. P - п.н..
Доказательство. Действительно, пусть  и Р (А) > 0. Тогда и Р (А) > 0. Тогда  , что противоречит предположению , что противоречит предположению  . .
§ 6. Сходимость последовательностей случайных величин по вероятности и почти наверное.
6.1. Пусть на  задано задано  последовательность случайных величин. последовательность случайных величин.
Определение. Последовательность случайных величин  называется сходящейся по вероятности к случайной величине называется сходящейся по вероятности к случайной величине  , обозначается , обозначается 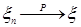 или или  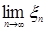 , если для , если для  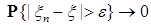 при при 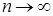 . .
Теорема 14. Последовательность случайных величин  сходится по вероятности к случайной величине сходится по вероятности к случайной величине  тогда и только тогда, когда тогда и только тогда, когда  при при  . .
6.2. Определение. Последовательность случайных величин  называется сходящейся с вероятностью 1 к случайной величине называется сходящейся с вероятностью 1 к случайной величине  , если , если  , обозначается , обозначается  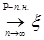 . .
Следующее утверждение хорошо известно [1].
Теорема 15. Справедливы следующие утверждения.
1) Для того, чтобы   , необходимо и достаточно, чтобы для любого , необходимо и достаточно, чтобы для любого   при при 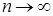 . .
2) Пусть   , тогда , тогда    . .
3) Пусть    ., тогда существует подпоследовательность ., тогда существует подпоследовательность  такая, что такая, что   . .
Замечание. Так как для любого 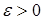   = =
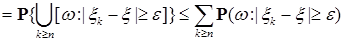 , то условие , то условие  является достаточным для сходимости является достаточным для сходимости   . .
6.3. Теорема 16. (Егорова) Пусть  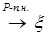 . Тогда для любого . Тогда для любого 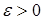 существует измеримое множество существует измеримое множество  такое, что такое, что  > >  , причем на множестве , причем на множестве  сходимость сходимость  равномерная. равномерная.
Задача. Докажите самостоятельно утверждение теоремы 16.
6.4. Мы часто будем использовать следующее утверждение.
Лемма 17. (Бореля-Кантелли) Пусть  последовательность событий и последовательность событий и 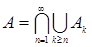 . Если . Если 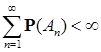 , то Р( А ) = 0. , то Р( А ) = 0.
Доказательство. В силу свойства вероятности имеем
Р (А) =   . .
Доказательство закончено.
Дата добавления: 2015-01-18 | Просмотры: 940 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 |
|

 , F) и (R1,B(R1)) - измеримые пространства.
, F) и (R1,B(R1)) - измеримые пространства. определенная (
определенная (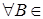 B(R1)
B(R1)  F (то есть, прообраз
F (то есть, прообраз 
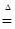
 является измеримым множеством в
является измеримым множеством в  ).
). =(Rn,B(Rn)), то B(Rn) – измеримые функции называются борелевскими.
=(Rn,B(Rn)), то B(Rn) – измеримые функции называются борелевскими.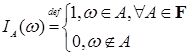
 представимая в виде
представимая в виде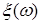
 (2)
(2)


 F называется дискретной. Если число слагаемых в сумме в (2) конечно, то случайная величина называется простой.
F называется дискретной. Если число слагаемых в сумме в (2) конечно, то случайная величина называется простой. . Требование измеримости важно. Действительно, если на (
. Требование измеримости важно. Действительно, если на ( , то в этом случае можно говорить о вероятности события, состоящего в том, что значение случайной величины принадлежит борелевскому множеству В.
, то в этом случае можно говорить о вероятности события, состоящего в том, что значение случайной величины принадлежит борелевскому множеству В. на (R,B(R)) с
на (R,B(R)) с 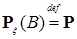
 на (R, B(R)).
на (R, B(R)).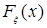
 Р
Р  , где
, где  R1, называется функцией распределения случайной величины
R1, называется функцией распределения случайной величины  .
. сосредоточена не более чем в счетном числе точек и может быть представлена в виде
сосредоточена не более чем в счетном числе точек и может быть представлена в виде 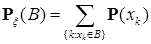 ,
, .
.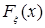 непрерывна. Случайная величина
непрерывна. Случайная величина  ,
,  обозначаемая
обозначаемая 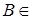 B(R1).
B(R1).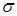 (e)=B(R1). Для того, чтобы
(e)=B(R1). Для того, чтобы  , для которых
, для которых  F. Известно, что:
F. Известно, что: , ii)
, ii)  , iii)
, iii) 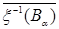 =
= 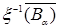 .
.
 D
D  , следовательно D=B(R1).
, следовательно D=B(R1). : R1
: R1 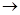 R1 - борелевская функция, а
R1 - борелевская функция, а  - случайная величина. Тогда сложная функция
- случайная величина. Тогда сложная функция  (то есть
(то есть 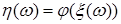 ) - случайная величина.
) - случайная величина.

 ,
,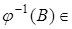 B(R1),
B(R1), 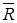 =
=  называется расширенной случайной величиной, если: для
называется расширенной случайной величиной, если: для  таких, что
таких, что 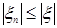 и
и  при
при  для всех
для всех  , то найдется последовательность простых случайных величин
, то найдется последовательность простых случайных величин 
 , и
, и 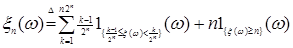
 для всех
для всех  , где
, где 
 .
. - последовательность расширенных случайных величин и
- последовательность расширенных случайных величин и  . Тогда
. Тогда  вида
вида 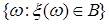 ,
,  –измеримая случайная величина. Тогда найдется борелевская функция
–измеримая случайная величина. Тогда найдется борелевская функция  . (Докажите самостоятельно.)
. (Докажите самостоятельно.)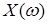 определенная на
определенная на  F). (3)
F). (3) - проекция Rn на
- проекция Rn на  -ую координату, то
-ую координату, то  , где
, где  . Ясно, что
. Ясно, что  - обычные случайные величины. Действительно, для
- обычные случайные величины. Действительно, для 
 R1,..,
R1,..,  R1,
R1,  R1
R1 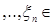 R1 }=
R1 }=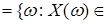 (R1
(R1  R1
R1  R1
R1  R1)
R1)  будет называться
будет называться 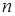 - мерным случайным вектором.
- мерным случайным вектором. есть случайный элемент в Rn. Действительно, если
есть случайный элемент в Rn. Действительно, если 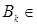 B(R1),
B(R1),  , то
, то 
 F, то наименьшая
F, то наименьшая  совпадает с B(Rn). поэтому для
совпадает с B(Rn). поэтому для  с
с 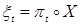 называется случайной функцией с временным интервалом Т.
называется случайной функцией с временным интервалом Т.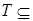 R1. Совокупность
R1. Совокупность  называется случайным процессом с временным интервалом Т. Если
называется случайным процессом с временным интервалом Т. Если  , то
, то 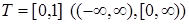 , то
, то 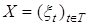 - называется случайным процессом с непрерывным временем.
- называется случайным процессом с непрерывным временем. - называется реализацией или траекторией процесса, соответствующего исходу
- называется реализацией или траекторией процесса, соответствующего исходу 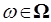 .
. - случайный процесс. Вероятностная мера Р на (RТ,B(RТ)) с P
- случайный процесс. Вероятностная мера Р на (RТ,B(RТ)) с P  P
P 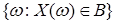 ,
,  B(RТ) называется распределением вероятностей процесса Х.
B(RТ) называется распределением вероятностей процесса Х. P
P  , где
, где  , называется конечномерными распределениями вероятностей случайного процесса
, называется конечномерными распределениями вероятностей случайного процесса  , где
, где  , называется конечномерными функциями распределения процесса
, называется конечномерными функциями распределения процесса  e
e  ) - измеримых пространств, где
) - измеримых пространств, где  - произвольное множество. Будем говорить, что
- произвольное множество. Будем говорить, что  - измеримые функции
- измеримые функции  независимы в совокупности, если для любого конечного набора
независимы в совокупности, если для любого конечного набора  элементы
элементы  - независимы, т.е. для
- независимы, т.е. для 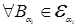 P
P  P
P  .
. были независимы в совокупности, необходимо и достаточно, чтобы для любого
были независимы в совокупности, необходимо и достаточно, чтобы для любого  Rn
Rn 
 , где
, где 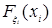
 . Докажите самостоятельно.
. Докажите самостоятельно. таких, что
таких, что  при
при  и
и  , а
, а 
 P (A k). Это определение корректно, так как оно не зависит от способа представления случайной величины
P (A k). Это определение корректно, так как оно не зависит от способа представления случайной величины  P
P  P.
P. . В силу теоремы 9 существует монотонная последовательность простых неотрицательных случайных величин
. В силу теоремы 9 существует монотонная последовательность простых неотрицательных случайных величин  таких, что
таких, что  при
при 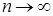 для каждого
для каждого  M
M  , поэтому существует
, поэтому существует  M
M  (причем он может принять значение
(причем он может принять значение  ).
). , обозначаемый М
, обозначаемый М 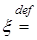
 называется математическим ожиданием случайной величины
называется математическим ожиданием случайной величины  , то
, то 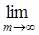 M
M  ).
). - простые неотрицательные случайные величины
- простые неотрицательные случайные величины 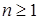 , причем
, причем  . Тогда
. Тогда  ≥ M
≥ M 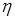 .
. и
и  . Ясно, что
. Ясно, что  и
и  ,
,

 , 1B
, 1B 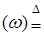
 ,
,  B
B 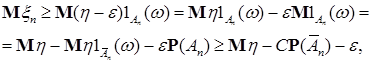
 .
. . Доказательство закончено.
. Доказательство закончено.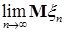
 . В силу симметрии имеем
. В силу симметрии имеем 
 . Отсюда вытекает корректность определения.
. Отсюда вытекает корректность определения.
 .
.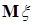 случайной величины
случайной величины  или
или  конечна, т.е.
конечна, т.е.  . В этом случае по определению полагается
. В этом случае по определению полагается  , а
, а  и
и  . Отсюда следует, что
. Отсюда следует, что  - конечно тогда и только тогда, когда
- конечно тогда и только тогда, когда  .
.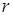 - порядка, где r = 1,2,…,k.
- порядка, где r = 1,2,…,k. и у случайной величины
и у случайной величины  , тогда существует
, тогда существует  и
и  .
. , где
, где  , следовательно
, следовательно  . Значит
. Значит 
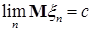
 , тогда
, тогда  .
. , то
, то  .
. , то из А) и В) следует, что
, то из А) и В) следует, что  , то есть
, то есть  .
. , то для каждого A
, то для каждого A 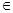 F существует
F существует  . Если
. Если 
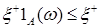 ,
, 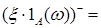
 .
. и
и 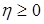 - случайные величины, причем
- случайные величины, причем 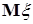
 и
и  , то
, то  .
. - последовательность простых функций таких, что
- последовательность простых функций таких, что 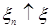 и
и  . Тогда
. Тогда  и
и 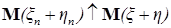 . Кроме того
. Кроме того  и
и  . Значит
. Значит 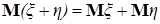 .
. , то
, то  .
. , Р- п.н. и
, Р- п.н. и  и
и 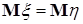 .
. , тогда
, тогда 
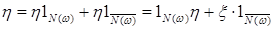 , где
, где 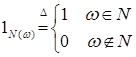 . В силу Е)
. В силу Е)  .
. , тогда
, тогда  Р - п.н.
Р - п.н. . Очевидно, что
. Очевидно, что  .
.  поэтому в силу свойства В)
поэтому в силу свойства В)  , следовательно
, следовательно  , значит
, значит  для всех
для всех 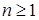 , но
, но 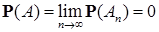 .
.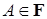

 . Тогда
. Тогда  . Тогда
. Тогда 
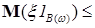
 . Поэтому
. Поэтому 
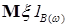 , тогда по свойству Е)
, тогда по свойству Е) 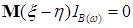 , а в силу Н)
, а в силу Н)  P - п.н., значит Р (В)=0.
P - п.н., значит Р (В)=0. P - п.н..
P - п.н.. и Р (А) > 0. Тогда
и Р (А) > 0. Тогда  , что противоречит предположению
, что противоречит предположению  задано
задано  последовательность случайных величин.
последовательность случайных величин. называется сходящейся по вероятности к случайной величине
называется сходящейся по вероятности к случайной величине 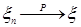 или
или 
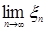 , если для
, если для 
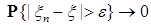 при
при  при
при  .
. , обозначается
, обозначается 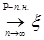 .
. , необходимо и достаточно, чтобы для любого
, необходимо и достаточно, чтобы для любого 
 при
при 
 такая, что
такая, что 
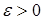

 =
=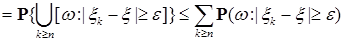 , то условие
, то условие  является достаточным для сходимости
является достаточным для сходимости 

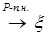 . Тогда для любого
. Тогда для любого  такое, что
такое, что  >
>  , причем на множестве
, причем на множестве  сходимость
сходимость  равномерная.
равномерная. последовательность событий и
последовательность событий и 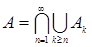 . Если
. Если 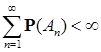 , то Р( А ) = 0.
, то Р( А ) = 0.
 .
.