Теоремы о предельном переходе под знаком интеграла
7.1. Теорема 18 (О монотонной сходимости) Пусть 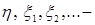
случайные величины. Тогда справедливы следующие утверждения:
а) если 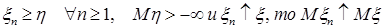 ; ;
б) если 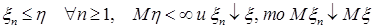 . .
Доказательство. а) Предположим, что 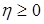 . Пусть для каждого . Пусть для каждого 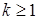 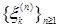 - последовательность простых случайных величин таких, что - последовательность простых случайных величин таких, что 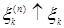 при при 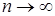 . Обозначим . Обозначим 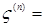 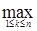  . Тогда очевидно, что . Тогда очевидно, что 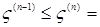 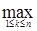 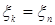 . Пусть . Пусть 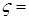 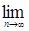 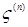 , поскольку для , поскольку для 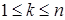 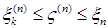 , то переходя к пределу при , то переходя к пределу при 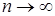 получим, что для любого получим, что для любого 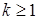 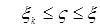 , значит , значит 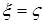 . Так как случайные величины . Так как случайные величины 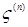 простые и простые и 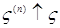 , то , то 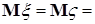 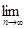 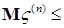 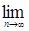 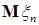 . .
С другой стороны, очевидно, что 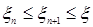 . Поэтому . Поэтому 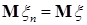 , значит , значит 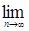 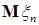 = = 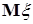 . .
Пусть теперь 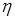 - случайная величина с - случайная величина с 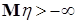 . Если . Если 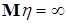 , то в силу свойства В) математических ожиданий , то в силу свойства В) математических ожиданий 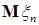 = = 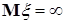 , утверждение доказано. , утверждение доказано.
Пусть 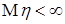 , тогда вместе с условием , тогда вместе с условием 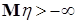 получаем: получаем: 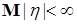 . Очевидно, что . Очевидно, что 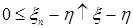 для всех для всех 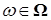 . Поэтому, согласно доказанному . Поэтому, согласно доказанному 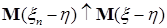 и значит по свойству Е) математических ожиданий и значит по свойству Е) математических ожиданий 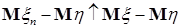 . Так как . Так как 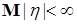 , то , то 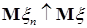 при при 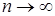 . .
Доказательство пункта б) следует из а), если вместо исходных случайных величин рассмотреть случайные величины со знаком минус.
7.2. Следствие 19. Пусть 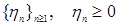 случайные величины. Тогда случайные величины. Тогда 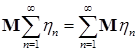 . .
7.3. Теорема 20 (Лемма Фату). Пусть 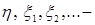 случайные величины. Тогда справедливы следующие утверждения: случайные величины. Тогда справедливы следующие утверждения:
а) если 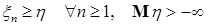 то то 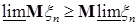 ; ;
б) если 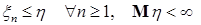 , то , то 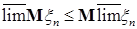 , ,
в) если 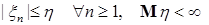 ,то ,то 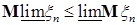 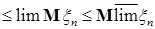 . .
Доказательство. а) Пусть 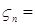 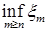 . Тогда . Тогда 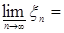 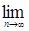 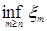 = = 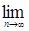 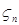 . Ясно, что . Ясно, что 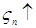 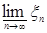 и и 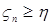 для всех для всех 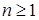 . Тогда по теореме 18 имеем . Тогда по теореме 18 имеем
М 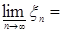 М М 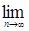 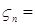 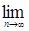 М М 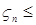 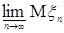 . Таким образом а) –доказано. . Таким образом а) –доказано.
Утверждения б) и в) доказываются аналогично.
7.4. Теорема 21 (Лебега о мажорируемой сходимости). Пусть 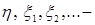 случайные величины такие, что P – п.н. случайные величины такие, что P – п.н. 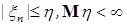 и и  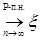 Тогда 1) Тогда 1) 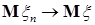 , 2) , 2) 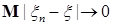 при при 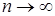 . .
Доказательство. По условию 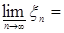 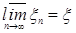 Р - п.н. Поэтому в силу пункта а) леммы Фату и по свойству G) математических ожиданий имеем М Р - п.н. Поэтому в силу пункта а) леммы Фату и по свойству G) математических ожиданий имеем М 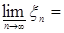 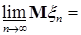 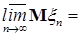 М М 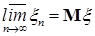 . Таким образом первое утверждение установлено, так как из неравенства . Таким образом первое утверждение установлено, так как из неравенства 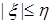 следует, что следует, что 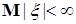 . .
Утверждение 2) доказывается также, если заметить, что 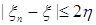 . .
Следствие 22. Пусть выполнены условия теоремы Лебега о мажорируемой сходимости и 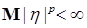 для р>1. Тогда для р>1. Тогда 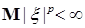 и и 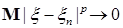 . .
Доказательство. Заметим, что 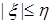 , , 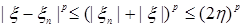 . Поэтому доказательство следует из теоремы 21. . Поэтому доказательство следует из теоремы 21.
7.5. Определение. Семейство случайных величин  называется интегрируемым (р.и.), если называется интегрируемым (р.и.), если 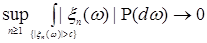 когда когда 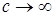 или или 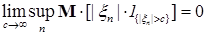 . .
Очевидно, что если последовательность 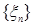 такая, что такая, что 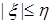 и и 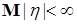 , то семейство , то семейство  - р.и.. Приведем критерий равномерной интегрируемости последовательности - р.и.. Приведем критерий равномерной интегрируемости последовательности  . .
Теорема 23. Последовательности  равномерно интегрируема тогда и только тогда, когда выполняются условия: равномерно интегрируема тогда и только тогда, когда выполняются условия:
i) для любого 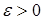 существует такое существует такое 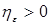 , что , что 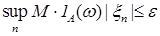 и и 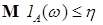 ; ;
ii) 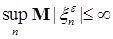 . .
Доказательство. Для любой положительной случайной величины 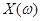 , множества , множества 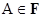 и всех и всех 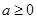 справедливо неравенство справедливо неравенство
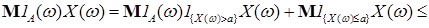 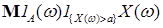 + + 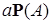 . .
Отсюда вытекает, что
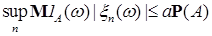 + + 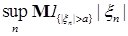 (4) (4)
Необходимость условия i) следует из (4), если в нем положить что 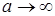
и Р (А) 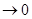 . Условие ii) следует из (4), если в нем положить . Условие ii) следует из (4), если в нем положить 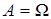 . .
Обратно. Сначала заметим, что для любой положительной случайной величины 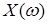 справедливо неравенство справедливо неравенство
М 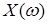 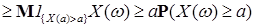 . (5) . (5)
Если выполнено ii), то в силу (5) имеем
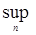 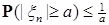 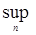 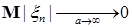 . .
Если выполнено i), то возьмем 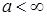 такое, что такое, что 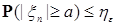 для любых для любых 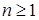 . Тогда . Тогда 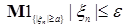 для всех для всех 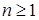 . Стало быть семейство . Стало быть семейство  -равномерно интегрируемо. Доказательство закончено. -равномерно интегрируемо. Доказательство закончено.
Предложение 24. Семейство случайных величин 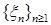 равномерно интегрируемо тогда и только тогда, когда равномерно интегрируемо тогда и только тогда, когда 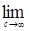 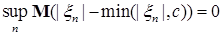 . .
Доказательство. Необходимость очевидна, так как 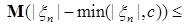 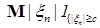 . .
Достаточность. Обозначим р(с) 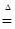 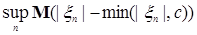 . Очевидно, что . Очевидно, что 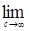 р(с) = 0. Заметим, что: р(с) = 0. Заметим, что:
1) 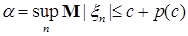 для всех с, поэтому для всех с, поэтому 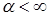 ; ;
2) 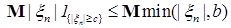 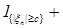 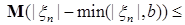
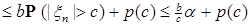 . (6) . (6)
Пусть 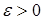 и выберем c таким, что р(c) и выберем c таким, что р(c) 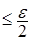 , а , а 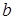 таким, что таким, что 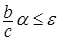 . Тогда в силу (6) . Тогда в силу (6) 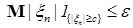 для любого n. Значит семейство равномерно интегрируемо. Доказательство закончено. для любого n. Значит семейство равномерно интегрируемо. Доказательство закончено.
7.6. Приведем теперь достаточное условие равномерной интегрируемости.
Теорема 25. Пусть  - последовательность интегрируемых случайных величин, а - последовательность интегрируемых случайных величин, а 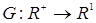 - возрастающая функция такая, что - возрастающая функция такая, что 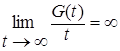 и и 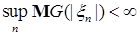 . Тогда семейство . Тогда семейство  - равномерно интегрируемо. - равномерно интегрируемо.
Доказательство. Пусть 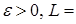 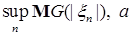 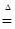 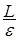 . Выберем для . Выберем для 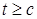 число число 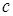 большим таким, что большим таким, что 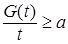 . Тогда . Тогда 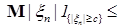 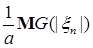 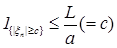 равномерно по n. Доказательство закончено. равномерно по n. Доказательство закончено.
Следствие 26. Пусть  последовательность случайных величин такая, что последовательность случайных величин такая, что 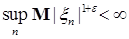 , где , где 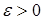 . Тогда последовательность . Тогда последовательность  - равномерно интегрируема. - равномерно интегрируема.
Доказательство. Действительно из неравенства 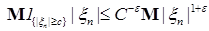 вытекает равномерная интегрируемость. Доказательство закончено. вытекает равномерная интегрируемость. Доказательство закончено.
Следствие 27. Пусть семейство случайных величин  - равномерно интегрируемо. Тогда - равномерно интегрируемо. Тогда 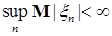 . .
Доказательство. Для фиксированного 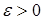 , имеем в силу теоремы 22 для любого конечного , имеем в силу теоремы 22 для любого конечного 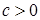
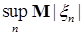 = =  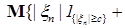 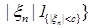 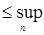 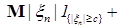
+ 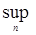 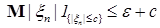 . Доказательство закончено. . Доказательство закончено.
7.6. Теорема 28. Пусть  - семейство равномерно интегрируемых случайных величин. Тогда справедливы утверждения. - семейство равномерно интегрируемых случайных величин. Тогда справедливы утверждения.
1) 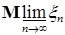 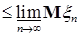 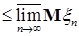 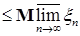 ; ;
2) Если  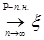 , тогда i) случайная величина , тогда i) случайная величина  - интегрируема, ii) - интегрируема, ii) 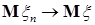 при при 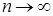 , iii) , iii) 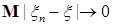 при при 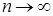 . .
Доказательство. а) Для всякого 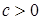
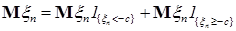 . (7) . (7)
В силу равномерной интегрируемости для 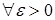 величину с можно выбрать сколь угодно большой, такой что величину с можно выбрать сколь угодно большой, такой что  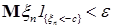 . Поэтому по лемме Фату . Поэтому по лемме Фату 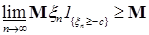 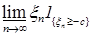 , но , но 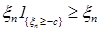 , значит , значит
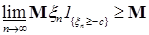 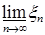 . (8) . (8)
Из (7) и (8) следует, что 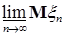 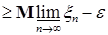 . В силу произвольности . В силу произвольности 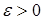 следует, что следует, что 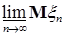 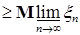 . Аналогичным образом доказываются другие неравенства. Утверждение пункта б) следует из а) в силу теоремы Лебега о мажорируемой сходимости. . Аналогичным образом доказываются другие неравенства. Утверждение пункта б) следует из а) в силу теоремы Лебега о мажорируемой сходимости.
7.7. Из теорем 23 и 28 следует утверждение.
Теорема 29. Пусть 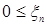 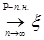 и и 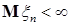 . Тогда . Тогда 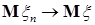 тогда и только тогда, когда тогда и только тогда, когда  - равномерно интегрируема. (Без доказательства) - равномерно интегрируема. (Без доказательства)
§ 8. Сходимость в пространстве Lp.
8.1. Определение. Множество действительных случайных величин 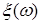 таких, что таких, что 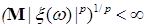 при при 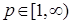 и и  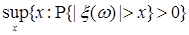 , при , при 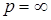 обозначим через обозначим через 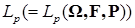 и в этом случае будем писать и в этом случае будем писать 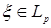 , , 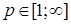 . Отметим, что . Отметим, что 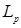 при при 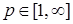 является банаховым пространством относительно нормы: является банаховым пространством относительно нормы: 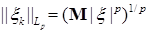 , при , при 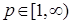 , , 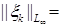 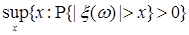 , при , при 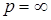 . .
Из этих определений следует, что: а) 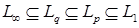 , если , если 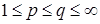 ; б) ; б) 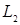 - является гильбертовым пространством относительно скалярного произведения - является гильбертовым пространством относительно скалярного произведения 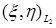 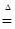 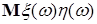 , где , где 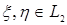 . .
8.2. Определение. Пусть  - последовательность случайных величин такая, что - последовательность случайных величин такая, что 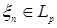 . Будем говорить, что . Будем говорить, что 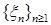 сходится в среднем порядка р к случайной величине сходится в среднем порядка р к случайной величине 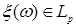 , если , если 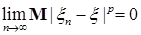 и использовать обозначение и использовать обозначение  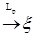 . .
В частности, если: 1) р=1 и 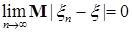 , то говорят, что , то говорят, что  сходится к сходится к  в среднем; 2) р=2 и в среднем; 2) р=2 и 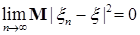 , то говорят, что , то говорят, что  сходится к сходится к  в среднеквадратическом смысле и обозначают в среднеквадратическом смысле и обозначают 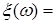 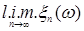 ; 3) при р = ; 3) при р =  сходимость называется существенно равномерной. сходимость называется существенно равномерной.
8.3. Приведем теперь без доказательства критерий Коши сходимости в 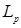 . .
Теорема 30. Пусть  последовательность из последовательность из 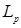 , , 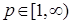 . Следующие утверждения эквивалентны: . Следующие утверждения эквивалентны:
1)  - сходящаяся в - сходящаяся в 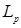 последовательность, последовательность,
2) 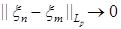 при при 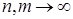 . .
8.4. Из результатов §7 следует утверждение.
Теорема 31. Пусть  последовательность из последовательность из 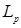 , , 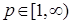 . Следующие утверждения эквивалентны: . Следующие утверждения эквивалентны:
1) последовательность 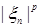 - равномерно интегрируема и - равномерно интегрируема и  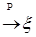 ; ;
2) 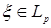 и и  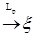 . .
Доказательство этого утверждения следует из неравенства 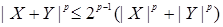 и теоремы 26. и теоремы 26.
8.5. Из теоремы 31 вытекают следующие утверждения.
Следствие 32. Пусть выполнены условия теоремы 31. Пусть существует 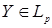 мажорирующая мажорирующая 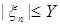 Р -п.н. Тогда следующие утверждения эквивалентны: Р -п.н. Тогда следующие утверждения эквивалентны:
1)  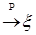 ; ;
2) 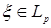 и и  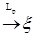 . .
Следствие 33. 1) Пусть 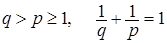 и и  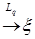 , тогда , тогда  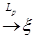 . .
2) Пусть 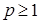 и и  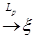 , тогда , тогда  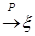 . .
8.6. Опишем теперь слабую сходимость в 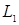 . .
Определение. Последовательность  с с 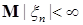 называется слабо сходящейся в называется слабо сходящейся в 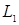 к случайной величине к случайной величине 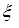 с с 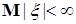 , если для любой ограниченной случайной величины , если для любой ограниченной случайной величины 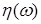 справедливо равенство справедливо равенство 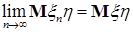 . .
Определение. Последовательность случайных величин  называется слабо компактной в называется слабо компактной в 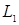 , если она содержит слабо сходящуюся подпоследовательность. , если она содержит слабо сходящуюся подпоследовательность.
Приведем критерий слабой компактности Данфорда-Петтиса.
Теорема 34. Для того чтобы последовательность случайных величин  с с 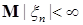 была слабо компактной в была слабо компактной в 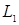 необходимо и достаточно, чтобы она была равномерно интегрируема. необходимо и достаточно, чтобы она была равномерно интегрируема.
Дата добавления: 2015-01-18 | Просмотры: 1347 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 |
|

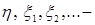
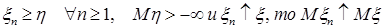 ;
;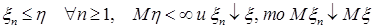 .
.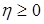 . Пусть для каждого
. Пусть для каждого 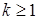
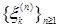 - последовательность простых случайных величин таких, что
- последовательность простых случайных величин таких, что 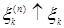 при
при 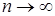 . Обозначим
. Обозначим 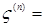
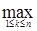
 . Тогда очевидно, что
. Тогда очевидно, что 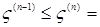
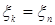 . Пусть
. Пусть 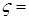
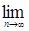
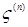 , поскольку для
, поскольку для 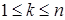
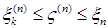 , то переходя к пределу при
, то переходя к пределу при 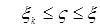 , значит
, значит 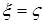 . Так как случайные величины
. Так как случайные величины 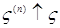 , то
, то 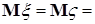
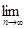
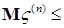
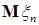 .
.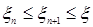 . Поэтому
. Поэтому 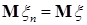 , значит
, значит 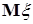 .
.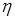 - случайная величина с
- случайная величина с 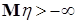 . Если
. Если 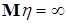 , то в силу свойства В) математических ожиданий
, то в силу свойства В) математических ожиданий 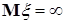 , утверждение доказано.
, утверждение доказано.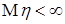 , тогда вместе с условием
, тогда вместе с условием 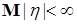 . Очевидно, что
. Очевидно, что 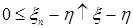 для всех
для всех 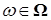 . Поэтому, согласно доказанному
. Поэтому, согласно доказанному 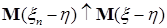 и значит по свойству Е) математических ожиданий
и значит по свойству Е) математических ожиданий 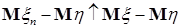 . Так как
. Так как 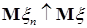 при
при 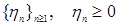 случайные величины. Тогда
случайные величины. Тогда 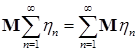 .
.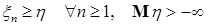 то
то 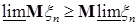 ;
;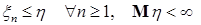 , то
, то 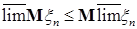 ,
,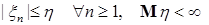 ,то
,то 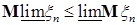
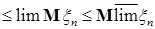 .
.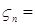
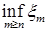 . Тогда
. Тогда 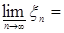
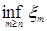 =
= 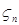 . Ясно, что
. Ясно, что 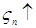
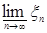 и
и 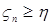 для всех
для всех 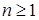 . Тогда по теореме 18 имеем
. Тогда по теореме 18 имеем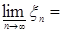 М
М 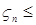
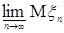 . Таким образом а) –доказано.
. Таким образом а) –доказано.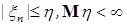 и
и 
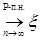 Тогда 1)
Тогда 1) 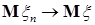 , 2)
, 2) 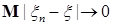 при
при 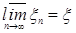 Р - п.н. Поэтому в силу пункта а) леммы Фату и по свойству G) математических ожиданий имеем М
Р - п.н. Поэтому в силу пункта а) леммы Фату и по свойству G) математических ожиданий имеем М 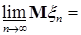
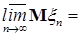 М
М 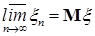 . Таким образом первое утверждение установлено, так как из неравенства
. Таким образом первое утверждение установлено, так как из неравенства 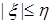 следует, что
следует, что 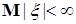 .
.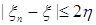 .
.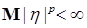 для р>1. Тогда
для р>1. Тогда 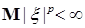 и
и 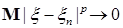 .
.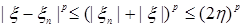 . Поэтому доказательство следует из теоремы 21.
. Поэтому доказательство следует из теоремы 21. называется интегрируемым (р.и.), если
называется интегрируемым (р.и.), если 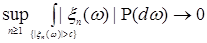 когда
когда 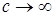 или
или 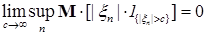 .
.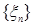 такая, что
такая, что 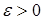 существует такое
существует такое 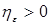 , что
, что 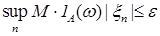 и
и 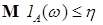 ;
;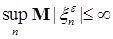 .
.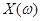 , множества
, множества 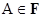 и всех
и всех 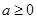 справедливо неравенство
справедливо неравенство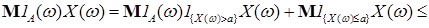
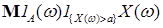 +
+ 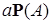 .
.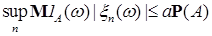 +
+ 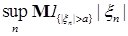 (4)
(4)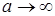
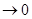 . Условие ii) следует из (4), если в нем положить
. Условие ii) следует из (4), если в нем положить 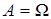 .
.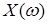 справедливо неравенство
справедливо неравенство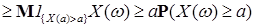 . (5)
. (5)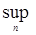
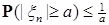
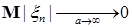 .
.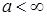 такое, что
такое, что 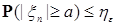 для любых
для любых 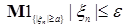 для всех
для всех 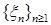 равномерно интегрируемо тогда и только тогда, когда
равномерно интегрируемо тогда и только тогда, когда 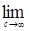
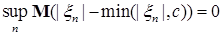 .
.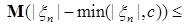
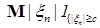 .
.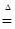
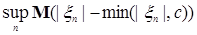 . Очевидно, что
. Очевидно, что 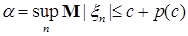 для всех с, поэтому
для всех с, поэтому 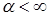 ;
;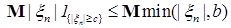
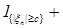
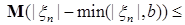
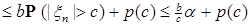 . (6)
. (6)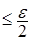 , а
, а 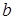 таким, что
таким, что 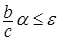 . Тогда в силу (6)
. Тогда в силу (6) 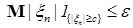 для любого n. Значит семейство равномерно интегрируемо. Доказательство закончено.
для любого n. Значит семейство равномерно интегрируемо. Доказательство закончено.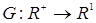 - возрастающая функция такая, что
- возрастающая функция такая, что 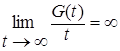 и
и 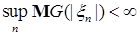 . Тогда семейство
. Тогда семейство 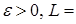
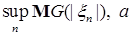
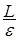 . Выберем для
. Выберем для 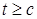 число
число 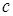 большим таким, что
большим таким, что 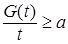 . Тогда
. Тогда 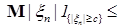
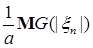
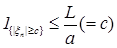 равномерно по n. Доказательство закончено.
равномерно по n. Доказательство закончено.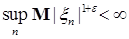 , где
, где 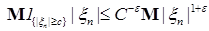 вытекает равномерная интегрируемость. Доказательство закончено.
вытекает равномерная интегрируемость. Доказательство закончено.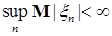 .
.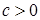
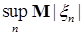 =
= 
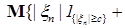
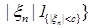
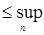
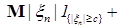
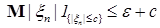 . Доказательство закончено.
. Доказательство закончено.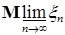
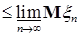
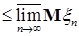
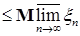 ;
;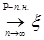 , тогда i) случайная величина
, тогда i) случайная величина  - интегрируема, ii)
- интегрируема, ii) 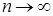 , iii)
, iii) 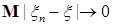 при
при 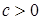
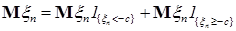 . (7)
. (7)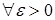 величину с можно выбрать сколь угодно большой, такой что
величину с можно выбрать сколь угодно большой, такой что 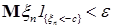 . Поэтому по лемме Фату
. Поэтому по лемме Фату 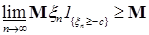
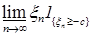 , но
, но 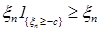 , значит
, значит 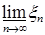 . (8)
. (8)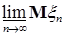
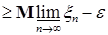 . В силу произвольности
. В силу произвольности 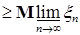 . Аналогичным образом доказываются другие неравенства. Утверждение пункта б) следует из а) в силу теоремы Лебега о мажорируемой сходимости.
. Аналогичным образом доказываются другие неравенства. Утверждение пункта б) следует из а) в силу теоремы Лебега о мажорируемой сходимости.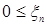
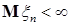 . Тогда
. Тогда 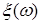 таких, что
таких, что 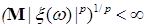 при
при 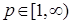 и
и 
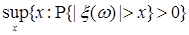 , при
, при 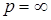 обозначим через
обозначим через 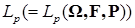 и в этом случае будем писать
и в этом случае будем писать 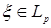 ,
, 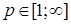 . Отметим, что
. Отметим, что 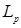 при
при 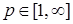 является банаховым пространством относительно нормы:
является банаховым пространством относительно нормы: 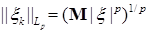 , при
, при 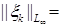
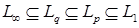 , если
, если 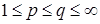 ; б)
; б) 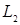 - является гильбертовым пространством относительно скалярного произведения
- является гильбертовым пространством относительно скалярного произведения 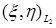
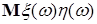 , где
, где 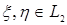 .
.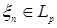 . Будем говорить, что
. Будем говорить, что 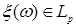 , если
, если 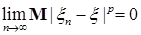 и использовать обозначение
и использовать обозначение 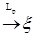 .
.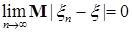 , то говорят, что
, то говорят, что  сходится к
сходится к 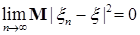 , то говорят, что
, то говорят, что 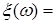
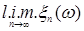 ; 3) при р =
; 3) при р =  сходимость называется существенно равномерной.
сходимость называется существенно равномерной.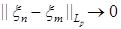 при
при 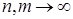 .
.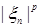 - равномерно интегрируема и
- равномерно интегрируема и 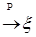 ;
;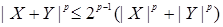 и теоремы 26.
и теоремы 26.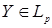 мажорирующая
мажорирующая 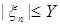 Р -п.н. Тогда следующие утверждения эквивалентны:
Р -п.н. Тогда следующие утверждения эквивалентны: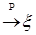 ;
;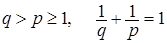 и
и 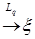 , тогда
, тогда 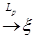 .
.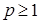 и
и 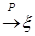 .
.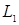 .
.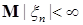 называется слабо сходящейся в
называется слабо сходящейся в 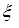 с
с 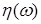 справедливо равенство
справедливо равенство 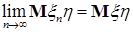 .
.