Измеримые пространства
Примеры 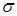 -алгебр: -алгебр:
1) 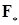 =(0, =(0, 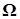 ) – бедная ) – бедная 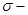 алгебра, алгебра,
2) 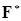 ={ A:A ={ A:A 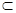 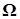 } - богатая } - богатая 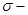 алгебра, алгебра,
3) 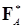 ={ A:, A, 0, ={ A:, A, 0, 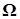 } называют алгеброй, порожденной множеством А. } называют алгеброй, порожденной множеством А.
Вопрос: Когда алгебра А (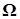 ) будет являться ) будет являться 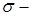 алгеброй F? алгеброй F?
Определение. Система М (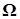 ) подмножеств ) подмножеств 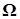 называется монотонным классом, если из того, что А называется монотонным классом, если из того, что А 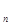 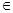 М ( М (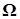 ) n=1,2,.. и ) n=1,2,.. и 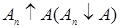 , т.е. , т.е. 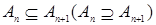 и и 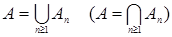 следует, что следует, что 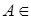 М ( М (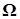 ). ).
Теорема 2. Для того, чтобы алгебра А (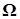 ) была ) была 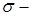 алгеброй F необходимо и достаточно, чтобы она являлась монотонным классом. алгеброй F необходимо и достаточно, чтобы она являлась монотонным классом.
2.1. Измеримое пространство (R1, B (R1))
Пусть R1 =(-  , ,  ] – действительная прямая и (a,b ] = { ] – действительная прямая и (a,b ] = { 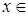 R1: R1: 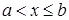 } для всех } для всех 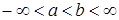 . Обозначим через А (R1) систему множеств в R1, состоящую из конечных сумм непересекающих интервалов вида (a,b ]: . Обозначим через А (R1) систему множеств в R1, состоящую из конечных сумм непересекающих интервалов вида (a,b ]: 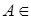 А (R1), где А (R1), где 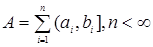 . Нетрудно видеть, что эта система множеств, а также . Нетрудно видеть, что эта система множеств, а также 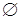 – образуют алгебру – А (R1), которая не является – образуют алгебру – А (R1), которая не является 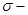 алгеброй, так как алгеброй, так как 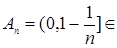 А (R1), но А (R1), но 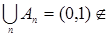 А (R1). А (R1).
Определение. B (R1) – наименьшая 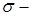 алгебра, порожденная А (R1) называется борелевской алгебра, порожденная А (R1) называется борелевской 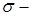 алгеброй, а ее множества – борелевскими. алгеброй, а ее множества – борелевскими.
Если обозначить через 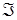 систему интервалов (a,b ], а через систему интервалов (a,b ], а через 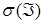 - наименьшую - наименьшую 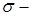 алгебру содержащую алгебру содержащую 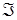 . Нетрудно установить B (R1)= . Нетрудно установить B (R1)= 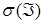 . .
Из каких элементов B (R1)? Из предыдущих построений следует, что B (R1) состоит из интервалов вида 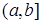 , где , где 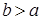 , и их счетных объединений и пересечений. Отсюда следует, что: , и их счетных объединений и пересечений. Отсюда следует, что:
i) 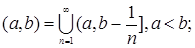 ii) ii) 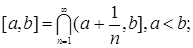 iii) iii) 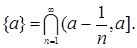
2.2. Измеримое пространство (Rn, B (Rn))
Пусть Rn = R 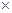 R R 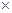 … … 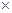 R – называется прямое или декартово произведение n экземпляров числовой прямой, то есть, множество упорядоченных наборов R – называется прямое или декартово произведение n экземпляров числовой прямой, то есть, множество упорядоченных наборов 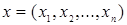 , где , где 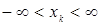 , , 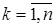 . .
Множество 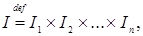 где где 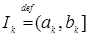 , называется прямоугольником, то есть, , называется прямоугольником, то есть, 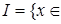 Rn: Rn: 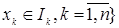 , а , а 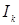 - его сторонами. - его сторонами.
Через 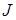 (Rn) обозначим совокупность всех прямоугольников из Rn. (Rn) обозначим совокупность всех прямоугольников из Rn. 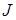 (Rn) - наименьшая (Rn) - наименьшая 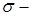 алгебра порожденная алгебра порожденная 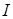 - называется борелевской - называется борелевской 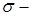 алгеброй множеств Rn, которую и обозначим через B (Rn). алгеброй множеств Rn, которую и обозначим через B (Rn).
2.3. Измеримое пространство (R 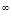 , B (R , B (R 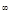 )) ))
R 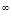 - пространство числовых последовательностей - пространство числовых последовательностей 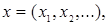 где - где - 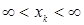 , , 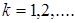 Пусть Пусть 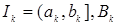 - борелевское множество к -ой числовой прямой (то есть, множество - борелевское множество к -ой числовой прямой (то есть, множество 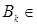 B (R1)). Рассмотрим множества: B (R1)). Рассмотрим множества:
i) 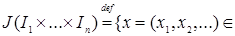 R R 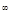 : : 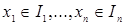 }; };
ii) 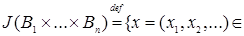 R R 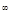 : : 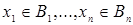 }; };
iii) 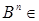 B (R B (R 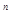 ) ) 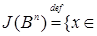 R R 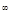 : : 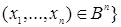 . .
Такие множества называются цилиндрическими, причем 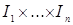 называют основанием цилиндра, а остальные координаты – образующими цилиндра. Нетрудно видеть, что множества называют основанием цилиндра, а остальные координаты – образующими цилиндра. Нетрудно видеть, что множества 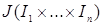 , , 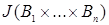 , , 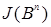 образуют алгебру. Обозначим наименьшие образуют алгебру. Обозначим наименьшие 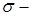 алгебры, порожденные множествами вида i)-iii) через B (R алгебры, порожденные множествами вида i)-iii) через B (R 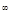 ), B 1(R ), B 1(R 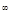 ), B 2(R ), B 2(R 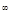 ), соответственно. Можно показать, что эти ), соответственно. Можно показать, что эти 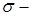 алгебры совпадают. алгебры совпадают.
2.4. Измеримое пространство (RТ , B (RТ))
Пусть Т 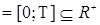 – произвольное пространство, множество. Пространство RТ – совокупность действительных функций на T со значениями в R1, обозначенные – произвольное пространство, множество. Пространство RТ – совокупность действительных функций на T со значениями в R1, обозначенные 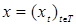 . Для простоты будем считать, что . Для простоты будем считать, что 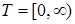 . Обозначим: . Обозначим: 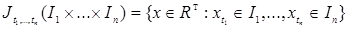 , где , где 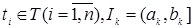 . Проводя рассуждения аналогичные приведенным в пункте 2.3, легко построить . Проводя рассуждения аналогичные приведенным в пункте 2.3, легко построить 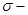 алгебру борелевских множеств на RТ, порожденную цилиндрическими множествами алгебру борелевских множеств на RТ, порожденную цилиндрическими множествами 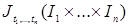 и обозначаемую через B (RТ). и обозначаемую через B (RТ).
Возникает вопрос: какова структура множества 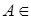 B (RТ)? Оказывается, что любое множество B (RТ)? Оказывается, что любое множество 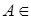 B (RТ) допускает представление B (RТ) допускает представление 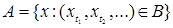 , где , где 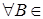 B (R B (R 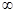 ). Отсюда следует, что множества, зависящие от поведения функций в несчетном числе точек t ). Отсюда следует, что множества, зависящие от поведения функций в несчетном числе точек t 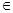 Т необязаны быть измеримыми относительно B (RТ). Например: i) Т необязаны быть измеримыми относительно B (RТ). Например: i) 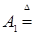 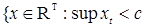 }, }, 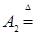 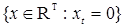 , ,
ii) 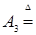 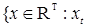 - непрерывные в точке - непрерывные в точке 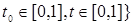 . .
В связи с неизмеримостью некоторых множеств из RТ по отношению к B (RТ) естественно рассматривать более узкие функциональные пространства.
2.5. Измеримое пространство (С[0,T], B (С[0,T])).
Пусть Т =[0,1], С [0,1] - пространство непрерывных функций xt, t  [0,1], со значениями в R1. Очевидно, С [0,1] –метрическое пространство, относительно метрики ρ(х,у)= [0,1], со значениями в R1. Очевидно, С [0,1] –метрическое пространство, относительно метрики ρ(х,у)= 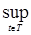 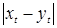 , то есть ρ(х,у) – расстояние между двумя непрерывными функциями, обладающие свойствами: , то есть ρ(х,у) – расстояние между двумя непрерывными функциями, обладающие свойствами:
1) ρ (х,у)= 0 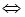 x=y; 2) ρ (х,у)= ρ (у,x); 3) ρ (х,у) x=y; 2) ρ (х,у)= ρ (у,x); 3) ρ (х,у) 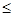 ρ (x,z)+ ρ(z,y). ρ (x,z)+ ρ(z,y).
Через B (С[0,T]) обозначим наименьшую 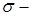 алгебру, порожденную цилиндрическими множествами, которые строятся аналогично пункту 2.4. алгебру, порожденную цилиндрическими множествами, которые строятся аналогично пункту 2.4.
2.6. Измеримое пространство (D,B(D)).
D – пространство функций xt, t  [0,1], со значениями в R1, непрерывные справа, имеющие пределы слева в любой точке t [0,1], со значениями в R1, непрерывные справа, имеющие пределы слева в любой точке t  [ 0,1 ]. В нем также можно ввести метрику: [ 0,1 ]. В нем также можно ввести метрику:
ρs(x,y) 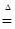 inf { inf { 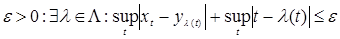 , ,
где 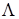 - множество строго возрастающих непрерывных на отрезке [0,1] функций - множество строго возрастающих непрерывных на отрезке [0,1] функций 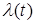 , причем , причем 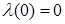 и и 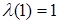 }. }. 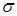 -алгебра B(D) строится аналогично пункту 2.4. -алгебра B(D) строится аналогично пункту 2.4.
§ 3. Задание вероятностных мер на измеримых пространствах.
3.1. Измеримое пространство (R1,B(R1)).
Пусть F: R1 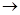 [0,1] - измеримая функция, обладающая свойствами: [0,1] - измеримая функция, обладающая свойствами:
1) неубывающая;
2) F(-  )= 0 F( )= 0 F( )= 1, где F(- )= 1, где F(-  )= )= 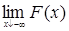 и F( и F( ) = ) = 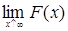 ; ;
3) непрерывна справа и имеет предел слева в каждой точке 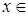 R1. R1.
Определение. Всякая функция F(x), удовлетворяющая свойствам 1)- 3) называется функцией распределения на R1.
Теорема 3. Пусть 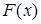 - функция распределения на R1, тогда на (R1, B(R1)) существует и притом единственная вероятностная мера Р такая, что для любых - функция распределения на R1, тогда на (R1, B(R1)) существует и притом единственная вероятностная мера Р такая, что для любых 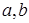 , причем , причем 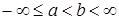 , Р , Р 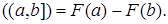
Пример: пусть функция распределения 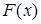 имеет вид: имеет вид:
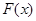 = = 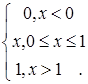
Соответствующую ей меру называют мерой Лебега отрезка 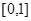 и обозначают Λ, причем Λ и обозначают Λ, причем Λ 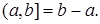
Приведем классификацию мер на (R1, B (R1)).
3.1.1. Дискретные меры.
Пусть 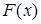 - функция распределения кусочно-постоянна и меняет свои значения в точках - функция распределения кусочно-постоянна и меняет свои значения в точках  х1,х2, …, причем х1,х2, …, причем 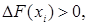 где где 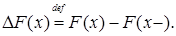 Ясно, что соответствующая этой функции распределения вероятностная мера Р сосредоточена в точках х1,х2, …, причем Р Ясно, что соответствующая этой функции распределения вероятностная мера Р сосредоточена в точках х1,х2, …, причем Р 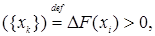 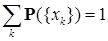 . .
Набор чисел 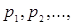 где где 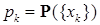 - называется дискретным распределением. - называется дискретным распределением.
Примеры дискретных распределений содержатся в приведенной ниже таблице.
| Распределение
| 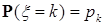
| Параметры
| | 1. Дискретное равномерное
| 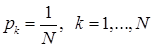
| 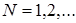
| | 2. Бернулли
| 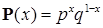
| 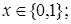 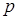 - вероятность успеха, - вероятность успеха, 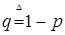
| 3. Биноминальное 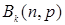
| 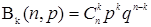
| 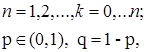 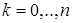 , ,
| 4. Пуассоновское Пк 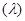
| Пk 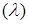 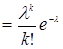
| 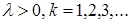
| 5. Геометрическое = 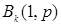
| 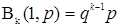
| 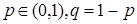 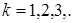
| 6. Отрицательное биноминальное 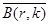
| 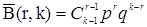
| 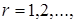 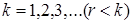 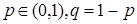
|
3.1.2. Абсолютно непрерывные меры.
Пусть существует неотрицательная функция 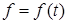 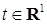 такая, что функция распределения такая, что функция распределения 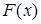 допускает представление: допускает представление: 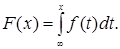
Функцию  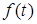 ( (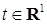 ) называют плотностью функции распределения ) называют плотностью функции распределения 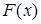 . .
Пример: Функцию 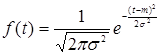 , , 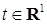 называют гауссовской плотностью. Легко убедиться в том, что называют гауссовской плотностью. Легко убедиться в том, что 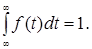
3.1.3. Сингулярные распределения.
Определение. Точка 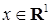 называется точкой роста функции распределения называется точкой роста функции распределения 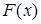 , если , если 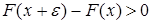 для любого для любого 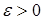 . .
Определение. Сингулярными мерами называются меры, функции распределения которых непрерывны, причем точки роста, которые образуют множество нулевой меры Лебега.
Пример. Возьмем отрезок 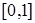 и построим на нем сингулярную функцию распределения и построим на нем сингулярную функцию распределения 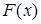 с помощью приема, принадлежащего Кантору Г. Пусть F o – функция распределения, соответствующая мере Лебега на отрезке [0,1].Разделим с помощью приема, принадлежащего Кантору Г. Пусть F o – функция распределения, соответствующая мере Лебега на отрезке [0,1].Разделим 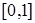 на 3 равные части и определим - функцию распределения на 3 равные части и определим - функцию распределения 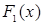 следующим образом: следующим образом:
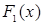 = 0, при x < 0; = 0, при x < 0; 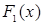 = = 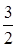 x, при x x, при x  [0, [0, 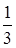 ); ); 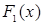 = = 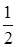 , при x , при x  [ [ 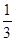 , , 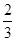 ); ); 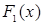 = = 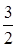 x – x – 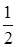 , при x , при x  [ [ 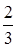 ,1); ,1);  = 1, при x > 1. Затем, каждый из интервалов = 1, при x > 1. Затем, каждый из интервалов 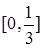 и и 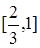 опять поделим на 3 равные части и определим функцию распределения опять поделим на 3 равные части и определим функцию распределения 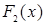 следующим образом: следующим образом:
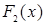 = 0, при x < 0; = 0, при x < 0; 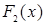 = = 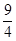 x, при x x, при x  [0, [0, 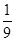 ); ); 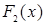 = = 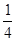 при x при x  [ [ 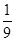 , , 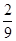 ]; ];  = = 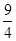 x - x - 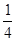 , при x , при x  [ [ 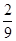 , , 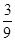 ]; ]; 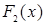 = = 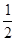 при x при x  [ [ 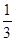 , , 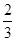 ); ); 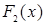 = = 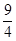 x – 1, при x x – 1, при x 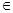 [ [ 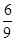 , , 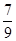 ); );  = = 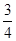 при x при x  [ [ 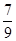 , , 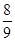 ); ); 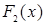 = = 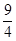 x - x - 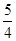 , при x , при x  [ [ 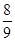 ,1]. ,1].
Продолжая этот процесс далее мы построим последовательность функции распределения 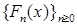 , которая, очевидно, сходится при , которая, очевидно, сходится при 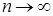 к некоторой неубывающей непрерывной функции распределения к некоторой неубывающей непрерывной функции распределения 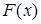 . Очевидно, что точки роста функции распределения . Очевидно, что точки роста функции распределения 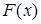 имеет нулевую меру Лебега, так как общая длина интервалов, на которых имеет нулевую меру Лебега, так как общая длина интервалов, на которых 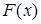 принимает постоянные значения равна 1. Действительно, общая длина интервалов постоянства функции принимает постоянные значения равна 1. Действительно, общая длина интервалов постоянства функции 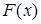 равна равна 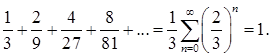
Пусть 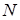 - множество точек роста функции распределения - множество точек роста функции распределения 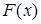 , тогда из последнего рассуждения следует, что , тогда из последнего рассуждения следует, что 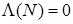 (в этих случаях говорят, что мера, соответствующая этой функции распределения сингулярна по отношению к мере Лебега (в этих случаях говорят, что мера, соответствующая этой функции распределения сингулярна по отношению к мере Лебега 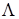 ). ).
Теорема 4. (Лебега) Любая функции распределения 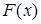 на прямой R1 представима в виде: на прямой R1 представима в виде:
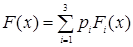 , ,
где 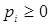 и и 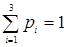 , а , а 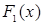 - дискретная, - дискретная, 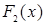 - абсолютно непрерывная, - абсолютно непрерывная, 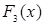 - сингулярная функции распределения. - сингулярная функции распределения.
3.2. Измеримое пространство (Rn,B(Rn)).
Пусть 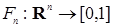 - измеримая функция, непрерывная справа (по совокупности измененных), имеющая левый предел. Введем оператор - измеримая функция, непрерывная справа (по совокупности измененных), имеющая левый предел. Введем оператор 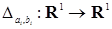 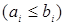 , действующей по правилу , действующей по правилу
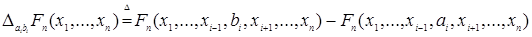 . .
Определение. Всякая непрерывная справа функция 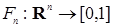 удовлетворяющая условиям: удовлетворяющая условиям:
1) 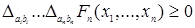 для любых для любых 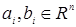 , i = , i = 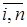 ; ;
2) 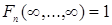 ; ;
3) 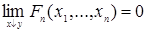 , если хотя бы одна из координат n-мерного вектора , если хотя бы одна из координат n-мерного вектора 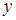 принимает значение принимает значение 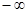 , ,
называется 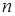 -мерной функцией распределения. -мерной функцией распределения.
Очевидно следующее утверждение.
Теорема 5. Пусть 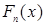 - - 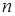 -мерная функция распределения. Тогда на (Rn,B(Rn)) существует единственная вероятностная мера Р такая, что -мерная функция распределения. Тогда на (Rn,B(Rn)) существует единственная вероятностная мера Р такая, что 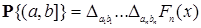 , где , где 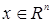 , , 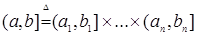 . .
Примеры. 1) Пусть
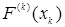 = = 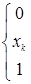 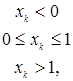
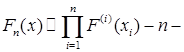 мерная функция распределения вероятностей, которой соответствует мера Лебега на мерная функция распределения вероятностей, которой соответствует мера Лебега на 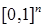 . .
2) 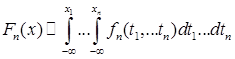 ,где ,где
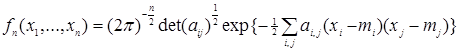 . .
3.3. Измеримое пространство (R 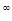 ,B(R ,B(R 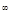 )) ))
Обозначим через 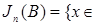 R R 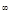 :( :(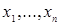 ) ) 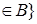 , где , где 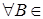 Rn – цилиндрическое множество в Rn – цилиндрическое множество в 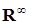 с основанием с основанием 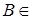 B(Rn). Пусть последовательность вероятностных мер B(Rn). Пусть последовательность вероятностных мер 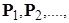 определенных, соответственно, на (R1, B(R1)), (R2, B(R2)), обладает следующим свойством: определенных, соответственно, на (R1, B(R1)), (R2, B(R2)), обладает следующим свойством:
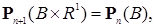 (1) (1)
где 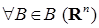 , , 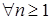 . .
Условие (1) называют условием (свойством) согласованности.
Теорема 5. (Колмогорова о продолжении вероятностной меры на (R 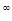 , B(R , B(R 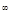 )). Пусть )). Пусть 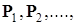 - последовательность вероятностных мер, соответственно, на (R1, B(R1)), (R2, B(R2)), обладающая свойством согласованности. Тогда существует единственная мера Р на (R - последовательность вероятностных мер, соответственно, на (R1, B(R1)), (R2, B(R2)), обладающая свойством согласованности. Тогда существует единственная мера Р на (R 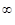 , B(R , B(R  )) такая, что для каждого )) такая, что для каждого 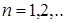 P P 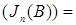 P P 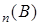 для для 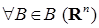 . .
3.4. Измеримое пространство (RТ , B(RТ))
Пусть Т=[0,T] 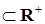 – произвольное множество индексов – произвольное множество индексов 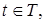 R t - числовая прямая, соответствующая индексу R t - числовая прямая, соответствующая индексу 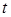 . Рассмотрим произвольный конечный неупорядоченный набор . Рассмотрим произвольный конечный неупорядоченный набор 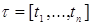 различных индексов различных индексов 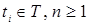 , и пусть P t - вероятностная мера на (R , и пусть P t - вероятностная мера на (R 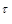 ,B(R ,B(R 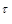 )), где R )), где R 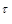 = R = R 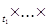 R R 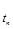 . .
Определение. Будем говорить, что семейство вероятностных мер 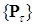 ( (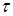 - пробегает множество всех конечных неупорядоченных наборов), является согласованным, если а) для любых двух наборов - пробегает множество всех конечных неупорядоченных наборов), является согласованным, если а) для любых двух наборов 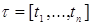 и и 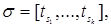 причем причем 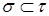 , выполняется равенство , выполняется равенство
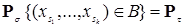 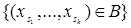 , ,
где 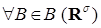 , б) выполнено (1). , б) выполнено (1).
Теорема 6. (Колмогорова о продолжении вероятностной меры на
(RТ ,B(RТ))). Пусть 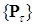 - согласованное семейство вероятностных мер на (R - согласованное семейство вероятностных мер на (R 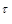 ,B(R ,B(R 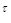 )). Тогда существует единственная вероятностная мера Р на (RТ ,B(RТ)) такая, что )). Тогда существует единственная вероятностная мера Р на (RТ ,B(RТ)) такая, что 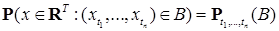 для всех неупорядоченных наборов для всех неупорядоченных наборов 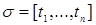 различных индексов различных индексов 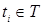 и и 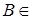 B(R B(R 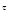 ). ).
Дата добавления: 2015-01-18 | Просмотры: 919 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 |
|

 -алгебр:
-алгебр: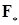 =(0,
=(0, 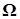 ) – бедная
) – бедная 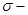 алгебра,
алгебра,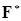 ={ A:A
={ A:A 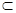
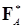 ={ A:, A, 0,
={ A:, A, 0, 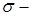 алгеброй F?
алгеброй F?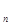
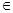 М (
М (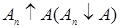 , т.е.
, т.е. 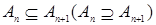 и
и 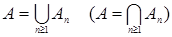 следует, что
следует, что 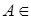 М (
М ( ,
, 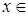 R1:
R1: 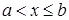 } для всех
} для всех 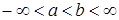 . Обозначим через А (R1) систему множеств в R1, состоящую из конечных сумм непересекающих интервалов вида (a,b ]:
. Обозначим через А (R1) систему множеств в R1, состоящую из конечных сумм непересекающих интервалов вида (a,b ]: 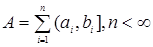 . Нетрудно видеть, что эта система множеств, а также
. Нетрудно видеть, что эта система множеств, а также  – образуют алгебру – А (R1), которая не является
– образуют алгебру – А (R1), которая не является 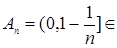 А (R1), но
А (R1), но 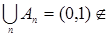 А (R1).
А (R1).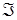 систему интервалов (a,b ], а через
систему интервалов (a,b ], а через 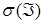 - наименьшую
- наименьшую 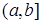 , где
, где 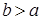 , и их счетных объединений и пересечений. Отсюда следует, что:
, и их счетных объединений и пересечений. Отсюда следует, что: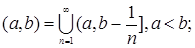 ii)
ii) 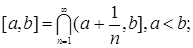 iii)
iii) 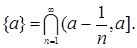
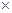 R
R 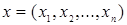 , где
, где 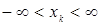 ,
, 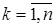 .
.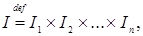 где
где 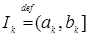 , называется прямоугольником, то есть,
, называется прямоугольником, то есть, 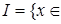 Rn:
Rn: 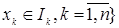 , а
, а 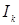 - его сторонами.
- его сторонами.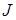 (Rn) обозначим совокупность всех прямоугольников из Rn.
(Rn) обозначим совокупность всех прямоугольников из Rn. 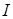 - называется борелевской
- называется борелевской 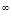 , B (R
, B (R 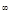 ))
))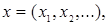 где -
где - 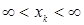 ,
, 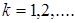 Пусть
Пусть 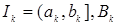 - борелевское множество к -ой числовой прямой (то есть, множество
- борелевское множество к -ой числовой прямой (то есть, множество 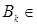 B (R1)). Рассмотрим множества:
B (R1)). Рассмотрим множества: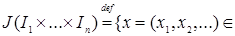 R
R 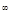 :
: 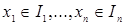 };
};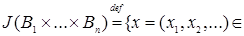 R
R 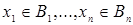 };
};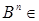 B (R
B (R 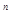 )
) 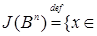 R
R 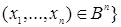 .
.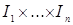 называют основанием цилиндра, а остальные координаты – образующими цилиндра. Нетрудно видеть, что множества
называют основанием цилиндра, а остальные координаты – образующими цилиндра. Нетрудно видеть, что множества 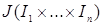 ,
, 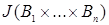 ,
, 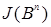 образуют алгебру. Обозначим наименьшие
образуют алгебру. Обозначим наименьшие 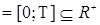 – произвольное пространство, множество. Пространство RТ – совокупность действительных функций на T со значениями в R1, обозначенные
– произвольное пространство, множество. Пространство RТ – совокупность действительных функций на T со значениями в R1, обозначенные 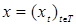 . Для простоты будем считать, что
. Для простоты будем считать, что 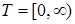 . Обозначим:
. Обозначим: 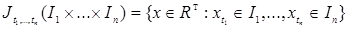 , где
, где 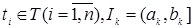 . Проводя рассуждения аналогичные приведенным в пункте 2.3, легко построить
. Проводя рассуждения аналогичные приведенным в пункте 2.3, легко построить 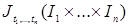 и обозначаемую через B (RТ).
и обозначаемую через B (RТ).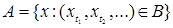 , где
, где 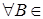 B (R
B (R 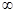 ). Отсюда следует, что множества, зависящие от поведения функций в несчетном числе точек t
). Отсюда следует, что множества, зависящие от поведения функций в несчетном числе точек t 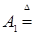
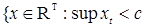 },
}, 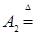
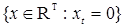 ,
,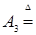
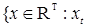 - непрерывные в точке
- непрерывные в точке 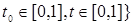 .
. [0,1], со значениями в R1. Очевидно, С [0,1] –метрическое пространство, относительно метрики ρ(х,у)=
[0,1], со значениями в R1. Очевидно, С [0,1] –метрическое пространство, относительно метрики ρ(х,у)= 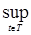
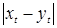 , то есть ρ(х,у) – расстояние между двумя непрерывными функциями, обладающие свойствами:
, то есть ρ(х,у) – расстояние между двумя непрерывными функциями, обладающие свойствами: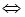 x=y; 2) ρ (х,у)= ρ (у,x); 3) ρ (х,у)
x=y; 2) ρ (х,у)= ρ (у,x); 3) ρ (х,у) 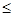 ρ (x,z)+ ρ(z,y).
ρ (x,z)+ ρ(z,y).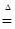 inf {
inf { 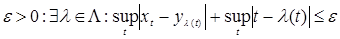 ,
, 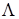 - множество строго возрастающих непрерывных на отрезке [0,1] функций
- множество строго возрастающих непрерывных на отрезке [0,1] функций 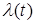 , причем
, причем 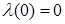 и
и 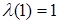 }.
}. 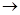 [0,1] - измеримая функция, обладающая свойствами:
[0,1] - измеримая функция, обладающая свойствами: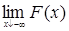 и F(
и F(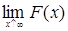 ;
;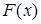 - функция распределения на R1, тогда на (R1, B(R1)) существует и притом единственная вероятностная мера Р такая, что для любых
- функция распределения на R1, тогда на (R1, B(R1)) существует и притом единственная вероятностная мера Р такая, что для любых 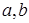 , причем
, причем 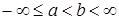 , Р
, Р 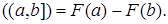
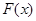 =
= 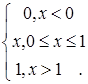
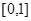 и обозначают Λ, причем Λ
и обозначают Λ, причем Λ 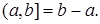
 х1,х2, …, причем
х1,х2, …, причем 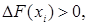 где
где 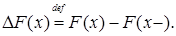 Ясно, что соответствующая этой функции распределения вероятностная мера Р сосредоточена в точках х1,х2, …, причем Р
Ясно, что соответствующая этой функции распределения вероятностная мера Р сосредоточена в точках х1,х2, …, причем Р 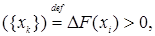
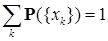 .
.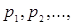 где
где 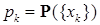 - называется дискретным распределением.
- называется дискретным распределением.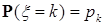
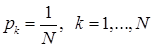
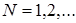
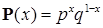
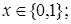
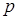 - вероятность успеха,
- вероятность успеха, 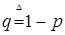
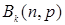
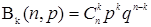
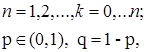
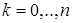 ,
,
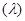
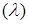
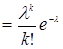
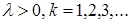
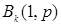
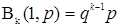
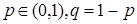
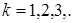
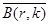
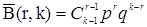
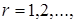
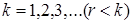
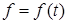
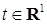 такая, что функция распределения
такая, что функция распределения 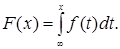
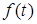 (
(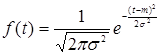 ,
, 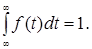
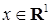 называется точкой роста функции распределения
называется точкой роста функции распределения 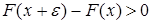 для любого
для любого 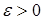 .
.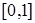 и построим на нем сингулярную функцию распределения
и построим на нем сингулярную функцию распределения 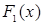 следующим образом:
следующим образом: 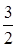 x, при x
x, при x 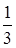 );
); 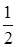 , при x
, при x 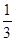 ,
, 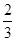 );
); 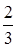 ,1);
,1); 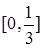 и
и 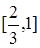 опять поделим на 3 равные части и определим функцию распределения
опять поделим на 3 равные части и определим функцию распределения 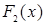 следующим образом:
следующим образом: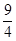 x, при x
x, при x 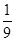 );
); 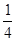 при x
при x 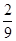 ];
]; 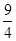 x -
x - 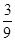 ];
]; 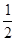 при x
при x 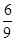 ,
, 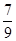 );
); 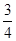 при x
при x 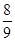 );
); 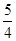 , при x
, при x 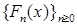 , которая, очевидно, сходится при
, которая, очевидно, сходится при 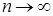 к некоторой неубывающей непрерывной функции распределения
к некоторой неубывающей непрерывной функции распределения 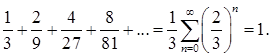
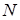 - множество точек роста функции распределения
- множество точек роста функции распределения 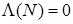 (в этих случаях говорят, что мера, соответствующая этой функции распределения сингулярна по отношению к мере Лебега
(в этих случаях говорят, что мера, соответствующая этой функции распределения сингулярна по отношению к мере Лебега 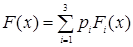 ,
,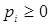 и
и 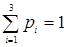 , а
, а 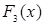 - сингулярная функции распределения.
- сингулярная функции распределения.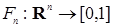 - измеримая функция, непрерывная справа (по совокупности измененных), имеющая левый предел. Введем оператор
- измеримая функция, непрерывная справа (по совокупности измененных), имеющая левый предел. Введем оператор 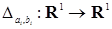
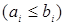 , действующей по правилу
, действующей по правилу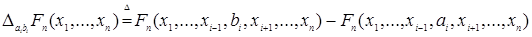 .
.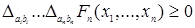 для любых
для любых 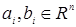 , i =
, i = 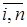 ;
;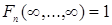 ;
;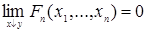 , если хотя бы одна из координат n-мерного вектора
, если хотя бы одна из координат n-мерного вектора 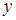 принимает значение
принимает значение 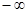 ,
,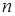 -мерной функцией распределения.
-мерной функцией распределения.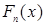 -
- 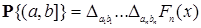 , где
, где 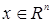 ,
, 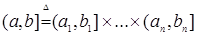 .
.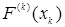 =
= 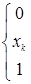
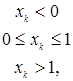
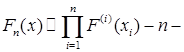 мерная функция распределения вероятностей, которой соответствует мера Лебега на
мерная функция распределения вероятностей, которой соответствует мера Лебега на  .
.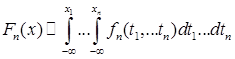 ,где
,где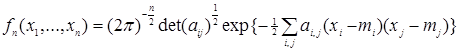 .
.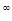 ,B(R
,B(R 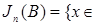 R
R 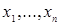 )
) 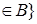 , где
, где 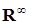 с основанием
с основанием 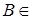 B(Rn). Пусть последовательность вероятностных мер
B(Rn). Пусть последовательность вероятностных мер 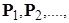 определенных, соответственно, на (R1, B(R1)), (R2, B(R2)), обладает следующим свойством:
определенных, соответственно, на (R1, B(R1)), (R2, B(R2)), обладает следующим свойством: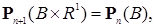 (1)
(1)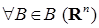 ,
, 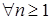 .
.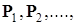 - последовательность вероятностных мер, соответственно, на (R1, B(R1)), (R2, B(R2)), обладающая свойством согласованности. Тогда существует единственная мера Р на (R
- последовательность вероятностных мер, соответственно, на (R1, B(R1)), (R2, B(R2)), обладающая свойством согласованности. Тогда существует единственная мера Р на (R 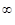 , B(R
, B(R  )) такая, что для каждого
)) такая, что для каждого 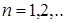 P
P 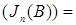 P
P 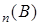 для
для  – произвольное множество индексов
– произвольное множество индексов 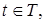 R t - числовая прямая, соответствующая индексу
R t - числовая прямая, соответствующая индексу 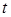 . Рассмотрим произвольный конечный неупорядоченный набор
. Рассмотрим произвольный конечный неупорядоченный набор 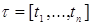 различных индексов
различных индексов 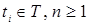 , и пусть P t - вероятностная мера на (R
, и пусть P t - вероятностная мера на (R 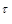 ,B(R
,B(R 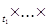 R
R 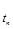 .
.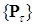 (
(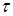 - пробегает множество всех конечных неупорядоченных наборов), является согласованным, если а) для любых двух наборов
- пробегает множество всех конечных неупорядоченных наборов), является согласованным, если а) для любых двух наборов 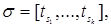 причем
причем 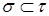 , выполняется равенство
, выполняется равенство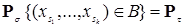
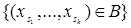 ,
,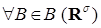 , б) выполнено (1).
, б) выполнено (1).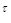 )). Тогда существует единственная вероятностная мера Р на (RТ ,B(RТ)) такая, что
)). Тогда существует единственная вероятностная мера Р на (RТ ,B(RТ)) такая, что 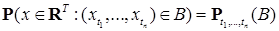 для всех неупорядоченных наборов
для всех неупорядоченных наборов 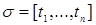 различных индексов
различных индексов 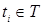 и
и 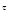 ).
).