|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Сходимость по распределению
9.1. Пусть на (Ω, F, P) задана последовательность Определение. Будем говорить, что Определение. Семейство вероятностных мер Из этих определений вытекает утверждение. Теорема 35. Пусть 9.2. Определение. Семейство вероятностных мер { P n}n > 1 на Определение. Семейство вероятностных мер { P n}n > 1 называется плотным, если для любого Приведем достаточное условие плотности семейства { P n}n > 1. Предложение 36. Если последовательность случайных величин
9.3. Следующее утверждение играет фундаментальную роль в теории слабой сходимости. Теорема 37 (Прохоров) Пусть { P n}n > 1 – семейство вероятностных мер на 9.4. Теорема 38. Справедливы следующие импликации: 1) 3) Доказательство этого утверждения можно найти например в [ 1 ].
Дата добавления: 2015-01-18 | Просмотры: 603 | Нарушение авторских прав |
 случайных элементов со значениями в
случайных элементов со значениями в  , где E - польское пространство, т.е. полное сепарабельное метрическое пространство, а
, где E - польское пространство, т.е. полное сепарабельное метрическое пространство, а  алгебра на E.
алгебра на E. со значениями в E сходится по распределению при
со значениями в E сходится по распределению при 
 к случайному элементу
к случайному элементу  со значениями в E и обозначать
со значениями в E и обозначать 


 Сb(E), где Сb(E) - пространство непрерывных ограниченных на E функций со значениями в R1, справедливо
Сb(E), где Сb(E) - пространство непрерывных ограниченных на E функций со значениями в R1, справедливо 
 на
на 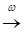 P 0 , если для любой
P 0 , если для любой  =
=  .
. - семейство случайных элементов, а
- семейство случайных элементов, а  соответствующее им семейство распределений
соответствующее им семейство распределений 
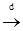
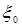 , тогда и только тогда, когда P n
, тогда и только тогда, когда P n 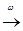 P о, т.е.
P о, т.е.  ), для
), для 
 >0 существует компакт
>0 существует компакт 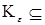 E такой, что
E такой, что  Рn (
Рn ( <
<  .
. , где
, где  >0, равномерно интегрируема, то семейство { P n}n > 1 плотно.
>0, равномерно интегрируема, то семейство { P n}n > 1 плотно.