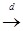|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
ВВЕДЕНИЕ. 9.1. Пусть на (Ω,F,P) задана последовательность случайных элементов со значениями в , где E- польское пространство9.1. Пусть на (Ω, F, P) задана последовательность Определение. Будем говорить, что Определение. Семейство вероятностных мер Из этих определений вытекает утверждение. Теорема 35. Пусть 9.2. Определение. Семейство вероятностных мер { P n}n > 1 на Определение. Семейство вероятностных мер { P n}n > 1 называется плотным, если для любого Приведем достаточное условие плотности семейства { P n}n > 1. Предложение 36. Если последовательность случайных величин
9.3. Следующее утверждение играет фундаментальную роль в теории слабой сходимости. Теорема 37 (Прохоров) Пусть { P n}n > 1 – семейство вероятностных мер на 9.4. Теорема 38. Справедливы следующие импликации: 1) 3) Доказательство этого утверждения можно найти например в [ 1 ].
ВВЕДЕНИЕ
Понятие «невроз» было введено в медицину в 1776 г. Cullen. Оно пришло на смену наивным представлениям гуморальной патологии о vapores (парах) как причине болезни и позволило связать ряд патологических состояний с вызвавшим их нарушением нервной деятельности. Таким образом, для своего времени это понятие было прогрессивным. В настоящее время в понятие «невроз» разными авторами вкладывается различное содержание. Со времени расцвета целлюлярной патологии ряд авторов в основу определения данного понятия берет морфологический критерий. Неврозами обозначались «заболевания нервной системы с неизвестной патологоанатомической основой», т. е. «без органических поражений, открываемых современными методами». А многие авторы, как, например, Wilson, автор трехтомного английского руководства по невропатологии, придерживаются этого взгляда и в настоящее время. Такое определение неврозов, основанное лишь на негативном признаке, зависящем к тому же от уровня развития техники исследования, является недостаточным; по меткому определению Axenfeld и Huchard, это — «незнание, возведенное в степень нозологической формы». Не удивительно, что до тех пор, пока не были выяснены причины столбняка, болезни Базедова и ряда других заболеваний, их относили в группу неврозов. Некоторые авторы, например К. М. Быков, пользовались термином «невроз» как широким общепатологическим понятием. «Неврозы,— по словам К. М. Быкова, — это начало всякого заболевания, какова бы ни была его причина». Под неврозом он понимал любое функциональное нарушение независимо от его причины. В таком понимании этот термин является синонимом функционального и неприменим для обозначения нозологической группы. Ряд авторов, исходя из взглядов И. П. Павлова, под термином «невроз» понимает те состояния патологически измененной высшей нервной деятельности, которые произошли вследствие перенапряжения или самих нервных процессов, или их подвижности. Перенапряжение нервных процессов может быть вызвано различными причинами, в том числе, как отмечала М. К. Петрова, действием химических веществ (хлористого кальция). Поэтому термин «невроз», рассматриваемый с такой точки зрения, становится широким патогенетическим понятием и также не применим для обозначения нозологической формы, выделенной на основе этиологического критерия. Некоторые клиницисты относят к неврозам все функциональные нарушения нервной деятельности как психогенной, так и соматогенной этиологии, не сопровождающиеся грубыми психическими нарушениями. Так, Б. В. Андреев рассматривал неврозы как заболевания, которые могут возникать под влиянием самых различных вредных факторов, в том числе травм, инфекций, эндокринных нарушений. Неврозы в таком понимании перестают быть нозологической группой и превращаются в этиологически разнородную группу, объединяемую по симптоматологическому признаку. Ряд авторов (Т. И. Юдин, В. Н. Мясищев, Е. А. Попов, О. В. Кербиков, А. В. Снежневский, А. А. Портнов, Д. Д. Федотов, Д. С. Озерецковский, А. М. Свядощ, С. Н. Доценко и Б. А. Первомайский) предлагают пользоваться термином «невроз» лишь для обозначения заболеваний, вызванных действием психической травмы, и относить их, таким образом, к психогенным заболеваниям, или психогениям. Последние делятся на две подгруппы: неврозы и психогенные или реактивные психозы. Граница между этими двумя подгруппами является условной. По традиции к неврозам относят истерию, хотя она может выражаться в виде не только параличей или расстройств чувствительности, но и сумеречных состояний, относимых к психозам. Предложение обозначать термином «неврозы» лишь заболевания психогенной этиологии целесообразно, и мы будем его придерживаться, исходя из того, что потребностям практики, в частности лечению и предупреждению болезней, наиболее отвечает классификация заболеваний, основанная на этиологическом принципе. Будет ли неврастенический симптомокомплекс являться следствием воздействия травмирующей психику ситуации, сифилитической инфекции или опухоли головного мозга, лечебные мероприятия при нем будут совершенно различными. Различны будут и пути профилактики. Естественно, что во всех этих случаях он должен быть отнесен к разным заболеваниям. В основе этиологической классификации лежит ведущая причина. На основании этиологического принципа давно выделены такие группы, как травматические и инфекционные заболевания головного мозга. Основываясь на этом же принципе, как указывалось нами (1959), можно выделить в особую нозологическую группу заболевания, вызванные сигнальным, т. е. информационным значением раздражителя. Постепенно мы пришли к убеждению, что это и есть психогении, или психогенные заболевания. Рассматривая как часть психогений неврозы человека, мы будем относить к последним функциональные нарушения нервной деятельности, вызванные психическими травмами, иначе говоря, раздражителями, действие которых определяется не их физическими параметрами, а информационным значением. В таком понимании невроз — болезнь, обусловленная действием информации. У человека раздражители, вызывающие заболевание вследствие своего информационного значения, это в основном условнорефлекторные раздражители, поэтому психогении, в том числе и неврозы, могут быть отнесены к заболеваниям, возникшим в результате действия условнорефлекторных раздражителей. Выделение в особую группу заболеваний, вызванных информационным действием раздражителей, позволит сделать классификацию болезней, построенную на этиологическом принципе, более целостной и в то же время отражающей основную причину этих болезней. Целью данной работы является описание этиологии, патогенеза, симптоматологии и терапии неврозов как группы заболеваний, обусловленных информационным действием раздражителей. Отсюда вытекает принципиальная возможность кибернетического подхода к проблеме неврозов в будущем. Дата добавления: 2015-01-18 | Просмотры: 771 | Нарушение авторских прав |
 случайных элементов со значениями в
случайных элементов со значениями в  , где E - польское пространство, т.е. полное сепарабельное метрическое пространство, а
, где E - польское пространство, т.е. полное сепарабельное метрическое пространство, а  алгебра на E.
алгебра на E. со значениями в E сходится по распределению при
со значениями в E сходится по распределению при 
 к случайному элементу
к случайному элементу  со значениями в E и обозначать
со значениями в E и обозначать 


 Сb(E), где Сb(E) - пространство непрерывных ограниченных на E функций со значениями в R1, справедливо
Сb(E), где Сb(E) - пространство непрерывных ограниченных на E функций со значениями в R1, справедливо 
 на
на 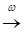 P 0 , если для любой
P 0 , если для любой  =
=  .
. - семейство случайных элементов, а
- семейство случайных элементов, а  соответствующее им семейство распределений
соответствующее им семейство распределений 
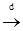
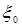 , тогда и только тогда, когда P n
, тогда и только тогда, когда P n 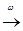 P о, т.е.
P о, т.е.  ), для
), для 
 >0 существует компакт
>0 существует компакт 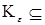 E такой, что
E такой, что  Рn (
Рn ( <
<  .
. , где
, где  >0, равномерно интегрируема, то семейство { P n}n > 1 плотно.
>0, равномерно интегрируема, то семейство { P n}n > 1 плотно.