 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Производные основных элементарных функций
Теорема 1. Пусть функция Доказательство. Заметим, что в условиях теоремы обратная функция Придадим значению
Пример 1. Найдем производные функций arcsin x, arccos x, arctg x, arcctg x / Решение. По теореме 1 имеем Аналогично,
Теорема 2. Если функции а) Доказательство. а) Пусть
б) Пусть
в) Пусть Теорема доказана. Следствия. 1) Если 2) Формула а) имеет место для любого конечного числа слагаемых. 3) Доказательство. 1) Поскольку 2) Например, имеем 3) Например, имеем В общем случае следствия 2) и 3) доказываются методом математической индукции. Рассмотрим показательно-степенную функцию
Таким образом,
Заметим, что в полученной формуле первое слагаемое есть результат дифференцирования Перейдем теперь к параметрическому заданию функций. Если зависимость функции у от аргумента х устанавливается не непосредственно, а с помощью некоторой третьей переменной t, называемой параметром, формулами
то говорят, что функция у от х задана параметрически. Если х и у рассматривать как прямоугольные координаты точки на плоскости, то уравнения (3.1) ставят в соответствие каждому значению
являются параметрическими уравнениями эллипса с полуосями а и b. Если в (3.1) уравнение
Найдем производную
Например, производная
Уравнение касательной к кривой, заданной параметрически, в точке
отсюда при
Аналогично из уравнения (1.5) получаем уравнение нормали:
Запишем теперь сводные таблицы производных основных элементарных функций и правил дифференцирования, полученных ранее. Правила дифференцирования 1. 5. Если 7. Если Таблица производных основных элементарных функций 1. 3. 5. 7. 9. 11.
Дата добавления: 2015-01-18 | Просмотры: 833 | Нарушение авторских прав |
 , непрерывна, строго монотонна на отрезке
, непрерывна, строго монотонна на отрезке 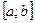 и дифференцируема во внутренней точке
и дифференцируема во внутренней точке  этого отрезка, причем
этого отрезка, причем 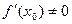 . Тогда обратная функция
. Тогда обратная функция 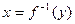 дифференцируема в точке
дифференцируема в точке 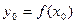 , причем
, причем 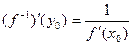 .
.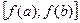 в силу теоремы из § 19 главы 1.
в силу теоремы из § 19 главы 1.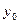 приращение
приращение 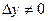 . Тогда
. Тогда 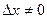 (так как функция
(так как функция 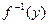 строго монотонна). Поэтому можно записать
строго монотонна). Поэтому можно записать 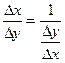 . Поскольку при
. Поскольку при 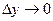 в силу непрерывности обратной функции и
в силу непрерывности обратной функции и 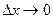 и, по условию, существует
и, по условию, существует 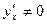 , имеем
, имеем 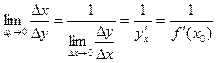 . Отсюда следует существование
. Отсюда следует существование  и равенство
и равенство 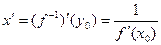 . Теорема доказана.
. Теорема доказана.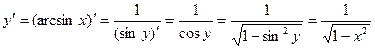 (поскольку
(поскольку  , имеем
, имеем  и корень берем со знаком плюс).
и корень берем со знаком плюс).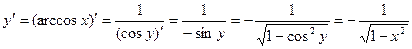 ,
,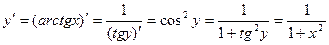 ,
, 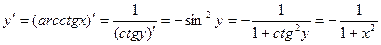 .
. и
и  имеют производные в точке
имеют производные в точке 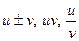 (если
(если 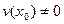 ) и справедливы формулы
) и справедливы формулы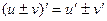 ; б)
; б) 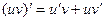 ; в)
; в) 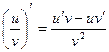 .
.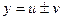 . Дадим
. Дадим 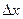 . Тогда функции u, v, y получат приращения
. Тогда функции u, v, y получат приращения 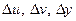 , причем
, причем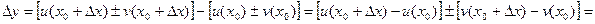
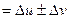 . Отсюда
. Отсюда 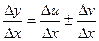 и
и 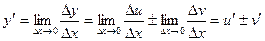 и равенство а) доказано.
и равенство а) доказано.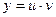 . Аналогично пункту а) имеем
. Аналогично пункту а) имеем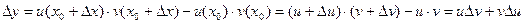 ,
, 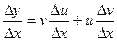 ,
, 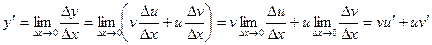 , т.е. имеет место формула б).
, т.е. имеет место формула б).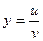 . Имеем
. Имеем 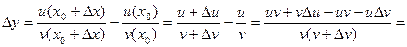
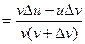 ,
, 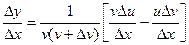 ,
, 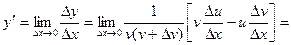
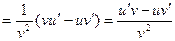 , т.е. имеет место формула в).
, т.е. имеет место формула в).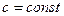 , то
, то 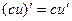 .
.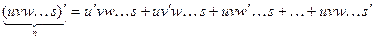 .
.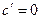 , имеем
, имеем 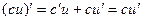 .
.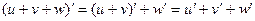 .
.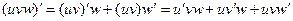 .
.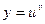 , где u и v – некоторые функции от х. Найдем производную функции у в точке, в которой дифференцируемы функции u и v. Для этого представим функцию у в виде
, где u и v – некоторые функции от х. Найдем производную функции у в точке, в которой дифференцируемы функции u и v. Для этого представим функцию у в виде 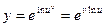 .По правилу дифференцирования сложной функции, в силу теоремы 2 и примера 1 § 1 имеем
.По правилу дифференцирования сложной функции, в силу теоремы 2 и примера 1 § 1 имеем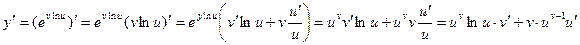 .
.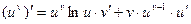 .
.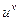 как показательной функции, а второе – как степенной функции. Примененный прием дифференцирования называется логарифмическим дифференцированием. Им бывает удобно пользоваться и тогда, когда дифференцируемая функция является произведением нескольких сомножителей.
как показательной функции, а второе – как степенной функции. Примененный прием дифференцирования называется логарифмическим дифференцированием. Им бывает удобно пользоваться и тогда, когда дифференцируемая функция является произведением нескольких сомножителей.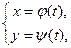
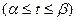 , (3.1)
, (3.1)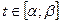 точку
точку 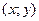 на плоскости. С изменением t точка
на плоскости. С изменением t точка 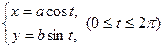 (3.2)
(3.2)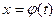 разрешается относительно t,
разрешается относительно t, 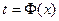 , то параметрическое задание функции можно свести к явному:
, то параметрическое задание функции можно свести к явному: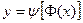 .
.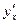 функции, заданной параметрически. Для этого предположим, что функции
функции, заданной параметрически. Для этого предположим, что функции 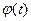 и
и 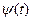 дифференцируемы, причем
дифференцируемы, причем 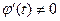 на некотором промежутке, а для функции
на некотором промежутке, а для функции 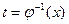 , имеющая конечную производную
, имеющая конечную производную 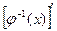 . Тогда по правилу дифференцирования сложной и обратной функций находим:
. Тогда по правилу дифференцирования сложной и обратной функций находим: 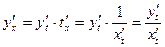 . Таким образом,
. Таким образом,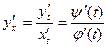 . (3.3)
. (3.3)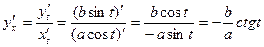 .
.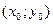 , соответствующей значению параметра
, соответствующей значению параметра 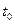 , получается из уравнения (1.4), если вместо
, получается из уравнения (1.4), если вместо 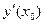 подставить
подставить 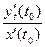 :
: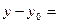

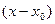 ,
,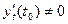 имеем
имеем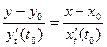 . (3.4)
. (3.4)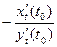
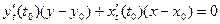 . (3.5)
. (3.5)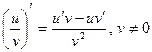 .
.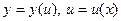 , то
, то 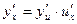 . 6. Если
. 6. Если 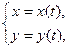 то
то 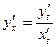 .
.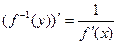 . 8.
. 8. 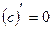 , где
, где 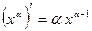 , в частности,
, в частности, 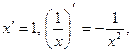
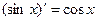 . 4.
. 4.  .
. 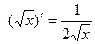 .
.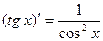 . 6.
. 6. 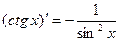 .
.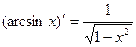 . 8.
. 8. 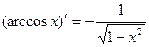 .
.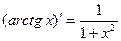 . 10.
. 10. 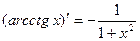 .
.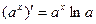 , в частности,
, в частности, 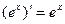 . 12.
. 12. 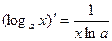 , в частности,
, в частности, 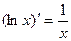 .
.