 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Производная сложной функции
Определение 1. Функция
где Теорема 1. Функция Доказательство. Необходимость. Пусть функция Достаточность. Пусть существует Теорема доказана. Замечание. Из теоремы 1 следует, что понятия функции, имеющей конечную производную, и дифференцируемой функции равносильны. Поэтому дифференцируемой можно назвать функцию, имеющую конечную производную, что и делают авторы некоторых учебников. Как связаны между собой свойства непрерывности и дифференцируемости функций? Имеет место Теорема 2.Если функция Доказательство. Поскольку в точке Теорема доказана. Обратное неверно, то есть существуют непрерывные функции, которые не дифференцируемы. Пример 1. Покажем, что функция Решение. Найдем приращение функции в точке В математическом анализе имеются примеры функций, которые в каждой точке числовой прямой непрерывны, но не дифференцируемы. Они имеют сложную конструкцию. Теорема 3. Пусть функция
Доказательство. Дадим значению
Отсюда
Заметим, что если Поскольку существует предел правой части равенства, то существует и предел левой части и
Теорема доказана. Замечание. Теорема 3 доказана для случая, когда сложная функция
Дата добавления: 2015-01-18 | Просмотры: 649 | Нарушение авторских прав |
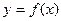 называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее приращение в этой точке представимо в виде
, если ее приращение в этой точке представимо в виде , (2.1)
, (2.1)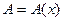 и не зависит от
и не зависит от 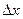 , а
, а 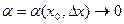 при
при 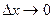 .
.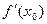 .
.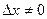 , получим
, получим  . Переходя к пределу при
. Переходя к пределу при 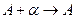 , т.е. предел правой части существует и равен А, значит, существует и предел левой части, т.е.
, т.е. предел правой части существует и равен А, значит, существует и предел левой части, т.е. 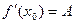 .
.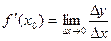 . Тогда по теореме 1 § 16 главы 1
. Тогда по теореме 1 § 16 главы 1 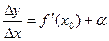 , где
, где 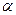 – бесконечно малая функция при
– бесконечно малая функция при 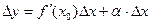 , т.е. функция дифференцируема в точке
, т.е. функция дифференцируема в точке  , имеем
, имеем  , что и означает непрерывность функции в точке
, что и означает непрерывность функции в точке 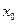 .
.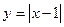 непрерывна, но не дифференцируема в точке
непрерывна, но не дифференцируема в точке  .
. . Поэтому
. Поэтому 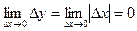 , то есть функция
, то есть функция 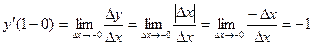 ,
, 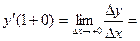
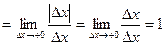 , то есть односторонние производные в точке
, то есть односторонние производные в точке 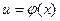 имеет в точке
имеет в точке  , функция
, функция  имеет в соответствующей точке
имеет в соответствующей точке 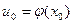 производную
производную 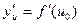 . Тогда сложная функция
. Тогда сложная функция 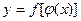 имеет в точке
имеет в точке  или, короче,
или, короче, 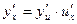 .
. функции
функции 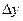 функции
функции 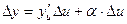 , где
, где  при
при  .
. .
.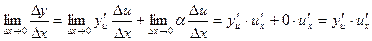 .
.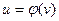 ,
,  , то
, то 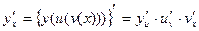 .
.