 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Производные и дифференциалы высших порядков
Поскольку производная Определение 1. Производная от производной функции
Могут встречаться и другие обозначения производных высших порядков. Производная Примеры производных порядка n: Выясним механический смысл 2-ой производной. Вычислим производную 2-го порядка функции, заданной параметрически уравнениями
Таким образом,
Определим дифференциалы высших порядков. Заметим, что в формуле Определение 2. Дифференциал от дифференциала функции Получим формулы для вычисления дифференциалов высших порядков функции
Из последней формулы получаем, что Сохраняется ли инвариантность формы дифференциалов высших порядков? Рассмотрим дифференциал 2-го порядка. Если х – функция, то
Если же х независимая переменная, то
Видим, что две последние формулы отличаются друг от друга слагаемым Таким образом, дифференциалы высших порядков свойством инвариантности формы не обладают.
Дата добавления: 2015-01-18 | Просмотры: 831 | Нарушение авторских прав |
 функции
функции  в свою очередь есть функция от х, по отношению к ней можно ставить вопрос о существовании и вычислении производной.
в свою очередь есть функция от х, по отношению к ней можно ставить вопрос о существовании и вычислении производной.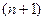 - го порядка. Производные, начиная со второй, называются производными высших порядков и обозначаются:
- го порядка. Производные, начиная со второй, называются производными высших порядков и обозначаются: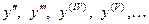 или
или 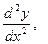
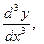
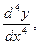
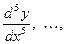
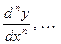 .
.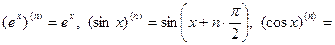
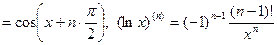 .
.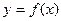 относительно аргумента х. Поэтому 2-я производная
относительно аргумента х. Поэтому 2-я производная 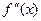 , как производная от производной, есть скорость изменения скорости, т.е. ускорение изменения функции
, как производная от производной, есть скорость изменения скорости, т.е. ускорение изменения функции 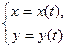
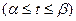 . Заметим, что
. Заметим, что 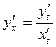 . Поступая так же, как при вычислении первой производной, получим
. Поступая так же, как при вычислении первой производной, получим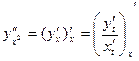
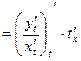 =
= 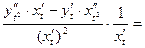
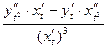 .
.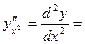
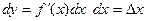 , т.е. от х не зависит,
, т.е. от х не зависит, 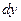 есть функция от х. Поэтому можно говорить о дифференциале от дифференциала
есть функция от х. Поэтому можно говорить о дифференциале от дифференциала 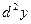 . Дифференциал от дифференциала 2-го порядка называется дифференциалом 3- го порядка и обозначается
. Дифференциал от дифференциала 2-го порядка называется дифференциалом 3- го порядка и обозначается 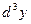 и т.д. Дифференциал от дифференциала (n -1)-го порядка называется дифференциалом n-го порядка и обозначается
и т.д. Дифференциал от дифференциала (n -1)-го порядка называется дифференциалом n-го порядка и обозначается 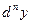 .
.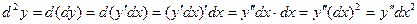 ,
,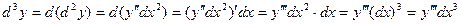 ,
,
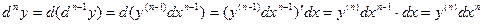 .
.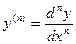 , т.е. обозначение
, т.е. обозначение 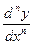 можно рассматривать не только как символ, но и как дробь.
можно рассматривать не только как символ, но и как дробь.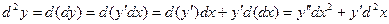 .
.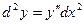 .
.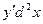 , т.е. уже для дифференциала 2-го порядка форма его изменяется при замене независимой переменной функцией.
, т.е. уже для дифференциала 2-го порядка форма его изменяется при замене независимой переменной функцией.