|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Основные теоремы о дифференцируемых функциях
Познакомившись в предыдущих параграфах с техникой дифференцирования функций, займемся теперь изучением связи между свойствами производной и свойствами функции. При этом будут существенно использоваться несколько теорем, называемых основными теоремами дифференциального исчисления или основными теоремами о дифференцируемых функциях. Поэтому сначала докажем их.
Теорема 1 (Ферма). Пусть функция 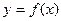 определена на промежутке Х и во внутренней точке определена на промежутке Х и во внутренней точке  этого промежутка принимает наибольшее или наименьшее значение. Тогда, если в точке этого промежутка принимает наибольшее или наименьшее значение. Тогда, если в точке  существует конечная производная, то она равна нулю, то есть существует конечная производная, то она равна нулю, то есть 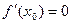 . .
Доказательство. Рассмотрим случай, когда 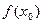 – наибольшее значение функции – наибольшее значение функции  на промежутке Х. Тогда на промежутке Х. Тогда 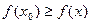 для всех для всех 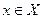 . По определению . По определению 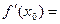 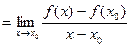 . Если . Если  справа, то справа, то 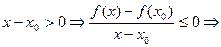  . Если . Если  слева, то слева, то 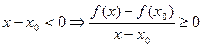 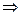 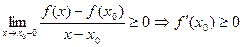 . Таким образом, одновременно должно быть . Таким образом, одновременно должно быть 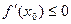 и и 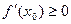 , что возможно только тогда, когда , что возможно только тогда, когда 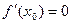 . .
Случай, когда 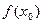 – наименьшее значение функции – наименьшее значение функции  на промежутке Х, рассматривается аналогично. на промежутке Х, рассматривается аналогично.
Геометрический смысл теоремы Ферма состоит в том, что в точке с абсциссой  касательная к кривой касательная к кривой 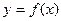 , если она существует, параллельна оси Ох.
Заметим, что в доказательстве теоремы существенно использовался тот факт, что точка , если она существует, параллельна оси Ох.
Заметим, что в доказательстве теоремы существенно использовался тот факт, что точка  – внутренняя, поскольку рассматривались точки х и правее, и левее точки – внутренняя, поскольку рассматривались точки х и правее, и левее точки  . .
| | Теорема доказана.
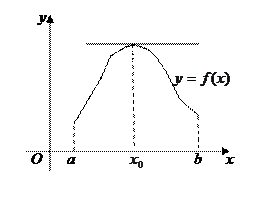
Пьер Ферма (1601-1665) занимался математикой на досуге, работая в Тулузе (Франция) юристом. Вместе с Паскалем является основателем математической теории вероятностей. Занимался также геометрией и теорией чисел. Наиболее известна «великая теорема Ферма», которая утверждает, что уравнение 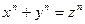 для для 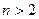 не имеет решений при натуральных значениях не имеет решений при натуральных значениях 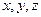 . Доказана эта теорема только в 1994 году. . Доказана эта теорема только в 1994 году.
Следующая теорема принадлежит Мишелю Роллю (1652-1719), французскому математику.
Теорема 2 (Ролля). Пусть функция 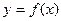 определена на отрезке определена на отрезке 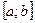 , причем: , причем:
1)  непрерывна на непрерывна на 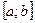 ; ;
2) в интервале 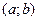 существует конечная производная существует конечная производная  ; ;
3) 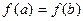 . .
Тогда в интервале 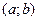 найдется точка с такая, что найдется точка с такая, что 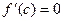 . .
Доказательство. Поскольку  непрерывна на отрезке непрерывна на отрезке 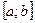 , то по 2-ой теореме Вейерштрасса она принимает на , то по 2-ой теореме Вейерштрасса она принимает на 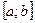 свое наибольшее значение М и наименьшее значение m. Возможны два случая: свое наибольшее значение М и наименьшее значение m. Возможны два случая:
1) М = m, т.е. 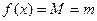 для всех для всех 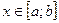 . Тогда . Тогда 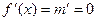 для всех для всех 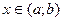 и в качестве с можно взять любую точку из и в качестве с можно взять любую точку из 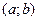 . .
2) 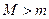 . Поскольку . Поскольку 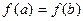 , то хотя бы одно из значений М или m функция принимает в интервале , то хотя бы одно из значений М или m функция принимает в интервале 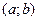 , т.е. в некоторой точке , т.е. в некоторой точке 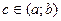 . Так как по условию . Так как по условию 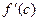 существует, то по теореме Ферма существует, то по теореме Ферма 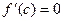 . .
Теорема доказана.
| | | | | | |  | | | | | Геометрически теорема Ролля означает, что если непрерывная кривая является графиком дифференцируемой функции, то между двумя точками кривой, имеющими одинаковую ординату, всегда найдется точка, в которой касательная параллельна оси Ох.
| | | |
Теорема 3 (Лагранжа). Пусть функция 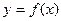 определена на отрезке определена на отрезке 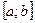 , причем: , причем:
1)  непрерывна на непрерывна на 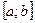 ; ;
2) в интервале 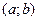 существует конечная производная существует конечная производная  . .
Тогда существует точка 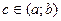 , такая, что , такая, что
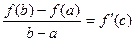 . (6.1) . (6.1)
Доказательство. Рассмотрим на 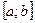 вспомогательную функцию вспомогательную функцию
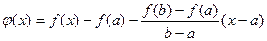 . .
Каждая из функций в правой части непрерывна на 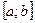 , дифференцируема в , дифференцируема в 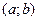 , поэтому и , поэтому и 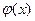 удовлетворяет этим же условиям. Кроме того, удовлетворяет этим же условиям. Кроме того,  , т.е. , т.е. 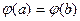 . Таким образом, функция . Таким образом, функция 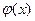 удовлетворяет условиям теоремы Роля, поэтому по этой теореме найдется точка удовлетворяет условиям теоремы Роля, поэтому по этой теореме найдется точка 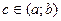 такая, что такая, что 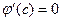 , т.е. , т.е.
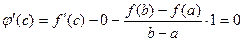 , ,
откуда
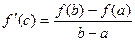 . .
Теорема доказана.
Формула (6.1) называется формулой Лагранжа. Ее часто используют в виде
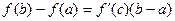 . (6.2) . (6.2)
Выясним геометрический смысл формулы Лагранжа.
| | | | | | | 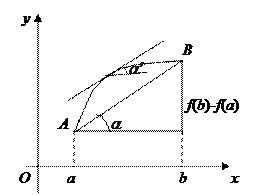 | | | | Рассмотрим дугу АВ кривой  и секущую АВ. Ясно, что и секущую АВ. Ясно, что 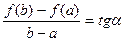 , где , где 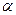 − угол между секущей АВ и осью Ох. Из геометрического смысла производной следует, что − угол между секущей АВ и осью Ох. Из геометрического смысла производной следует, что 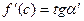 , где , где 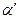 − угол между касательной к кривой в точке − угол между касательной к кривой в точке 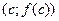 и осью Ох. Из формулы Лагранжа следует, что и осью Ох. Из формулы Лагранжа следует, что 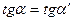 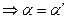 , т.е. на дуге АВ есть точка, в которой касательная параллельна секущей АВ. , т.е. на дуге АВ есть точка, в которой касательная параллельна секущей АВ.
| | | |
Жозеф Луи Лагранж (1736-1813) родился в Турине в итало-французской семье. В 19 лет стал профессором математики артиллерийской школы в Турине. В 1766 году был приглашен Фридрихом II в Берлин, написавшим в приглашении, что «необходимо, чтобы величайший геометр Европы проживал вблизи величайшего из королей». В 1786 году после смерти Фридриха II переехал в Париж. Занимался вариационным исчислением, алгеброй, теорией чисел, математическим анализом, небесной механикой.
Замечание. Теорема Ролля является частным случаем теоремы Лагранжа., когда 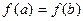 (секущая параллельна оси Ох). (секущая параллельна оси Ох).
Рассмотрим теперь не весь отрезок 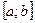 , а его часть , а его часть 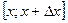 , где , где 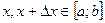 . Применим к отрезку . Применим к отрезку 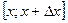 формулу Лагранжа: формулу Лагранжа: 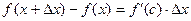 , где , где 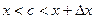 . Можно записать . Можно записать 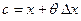 , где , где 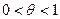 . (достаточно положить . (достаточно положить 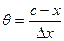 ). Тогда получим формулу ). Тогда получим формулу 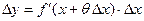 , называемую формулой конечных приращений. Эта формула устанавливает точное выражение для приращения функции при любом конечном значении приращения , называемую формулой конечных приращений. Эта формула устанавливает точное выражение для приращения функции при любом конечном значении приращения 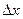 , в отличие от приближенной формулы , в отличие от приближенной формулы 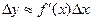 , в этих формулах в разных точках вычисляются значения производной. , в этих формулах в разных точках вычисляются значения производной.
Так как мы не знаем, чему равно с, то и значение 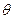 , как правило, нам неизвестно. Тем не менее, полученная формула находит большое применение в теоретических исследованиях. , как правило, нам неизвестно. Тем не менее, полученная формула находит большое применение в теоретических исследованиях.
Теорема 4 (Коши). Пусть на отрезке 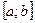 заданы функции заданы функции  и и  , причем: , причем:
1)  и и  непрерывны на непрерывны на 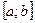 ; ;
2) в интервале 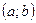 существуют производные существуют производные  и и 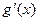 , ,  . .
Тогда существует точка 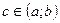 такая, что такая, что
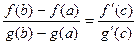 . .
Эта формула называется формулой Коши.
Доказательство. Заметим сначала, что формула имеет смысл. Действительно, 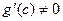 по условию. Кроме того, по условию. Кроме того, 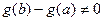 , так как в противном случае было бы , так как в противном случае было бы 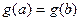 и по теореме Роля нашлась бы точка в интервале и по теореме Роля нашлась бы точка в интервале 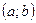 , в которой , в которой 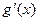 обратилась бы в нуль, а это невозможно по условию. обратилась бы в нуль, а это невозможно по условию.
Рассмотрим вспомогательную функцию 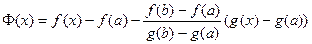 . Эта функция удовлетворяет условиям теоремы Роля: непрерывна на . Эта функция удовлетворяет условиям теоремы Роля: непрерывна на 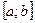 , дифференцируема в , дифференцируема в 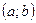 , , 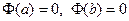 . Поэтому найдется точка . Поэтому найдется точка 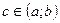 такая, что такая, что 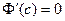 , т.е. , т.е. 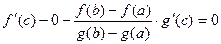 , откуда , откуда 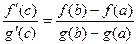 . .
Теорема доказана.
Замечания. 1) Теорема Лагранжа является частным случаем теоремы Коши при 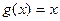 . .
2) Теоремы Роля, Лагранжа и Коши называют теоремами о средних значениях, поскольку в них идет речь о значениях производных при средних значениях аргумента (а и b – крайние, с – среднее значения). При этом теорему Коши часто называют обобщенной теоремой о среднем значении.
Дата добавления: 2015-01-18 | Просмотры: 873 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|

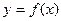 определена на промежутке Х и во внутренней точке
определена на промежутке Х и во внутренней точке  этого промежутка принимает наибольшее или наименьшее значение. Тогда, если в точке
этого промежутка принимает наибольшее или наименьшее значение. Тогда, если в точке 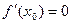 .
.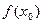 – наибольшее значение функции
– наибольшее значение функции  на промежутке Х. Тогда
на промежутке Х. Тогда 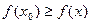 для всех
для всех 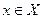 . По определению
. По определению 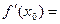
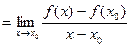 . Если
. Если  справа, то
справа, то 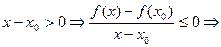
 . Если
. Если 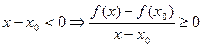
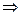
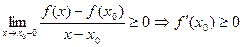 . Таким образом, одновременно должно быть
. Таким образом, одновременно должно быть 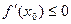 и
и 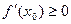 , что возможно только тогда, когда
, что возможно только тогда, когда 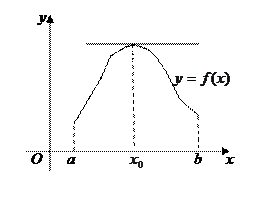
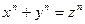 для
для 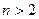 не имеет решений при натуральных значениях
не имеет решений при натуральных значениях 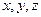 . Доказана эта теорема только в 1994 году.
. Доказана эта теорема только в 1994 году.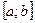 , причем:
, причем: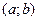 существует конечная производная
существует конечная производная  ;
;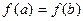 .
.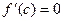 .
.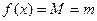 для всех
для всех 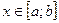 . Тогда
. Тогда 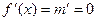 для всех
для всех 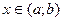 и в качестве с можно взять любую точку из
и в качестве с можно взять любую точку из 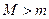 . Поскольку
. Поскольку 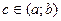 . Так как по условию
. Так как по условию 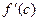 существует, то по теореме Ферма
существует, то по теореме Ферма 
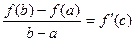 . (6.1)
. (6.1)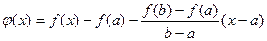 .
.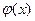 удовлетворяет этим же условиям. Кроме того,
удовлетворяет этим же условиям. Кроме того,  , т.е.
, т.е. 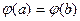 . Таким образом, функция
. Таким образом, функция 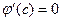 , т.е.
, т.е.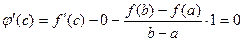 ,
,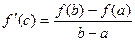 .
.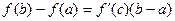 . (6.2)
. (6.2)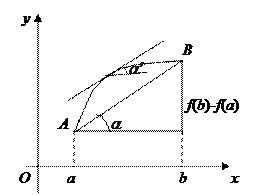
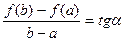 , где
, где 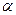 − угол между секущей АВ и осью Ох. Из геометрического смысла производной следует, что
− угол между секущей АВ и осью Ох. Из геометрического смысла производной следует, что 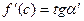 , где
, где 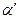 − угол между касательной к кривой в точке
− угол между касательной к кривой в точке 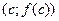 и осью Ох. Из формулы Лагранжа следует, что
и осью Ох. Из формулы Лагранжа следует, что 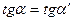
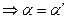 , т.е. на дуге АВ есть точка, в которой касательная параллельна секущей АВ.
, т.е. на дуге АВ есть точка, в которой касательная параллельна секущей АВ.
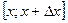 , где
, где 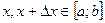 . Применим к отрезку
. Применим к отрезку 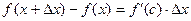 , где
, где 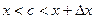 . Можно записать
. Можно записать 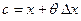 , где
, где 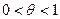 . (достаточно положить
. (достаточно положить 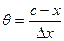 ). Тогда получим формулу
). Тогда получим формулу 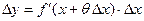 , называемую формулой конечных приращений. Эта формула устанавливает точное выражение для приращения функции при любом конечном значении приращения
, называемую формулой конечных приращений. Эта формула устанавливает точное выражение для приращения функции при любом конечном значении приращения 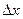 , в отличие от приближенной формулы
, в отличие от приближенной формулы 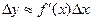 , в этих формулах в разных точках вычисляются значения производной.
, в этих формулах в разных точках вычисляются значения производной.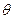 , как правило, нам неизвестно. Тем не менее, полученная формула находит большое применение в теоретических исследованиях.
, как правило, нам неизвестно. Тем не менее, полученная формула находит большое применение в теоретических исследованиях. , причем:
, причем: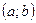 существуют производные
существуют производные 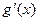 ,
,  .
.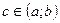 такая, что
такая, что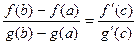 .
.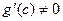 по условию. Кроме того,
по условию. Кроме того, 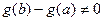 , так как в противном случае было бы
, так как в противном случае было бы 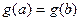 и по теореме Роля нашлась бы точка в интервале
и по теореме Роля нашлась бы точка в интервале 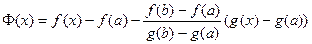 . Эта функция удовлетворяет условиям теоремы Роля: непрерывна на
. Эта функция удовлетворяет условиям теоремы Роля: непрерывна на 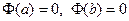 . Поэтому найдется точка
. Поэтому найдется точка 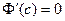 , т.е.
, т.е. 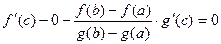 , откуда
, откуда 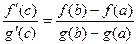 .
.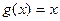 .
.