 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Метод наименьших квадратов ( МНК )4. Пути реализации целей занятия:
Для реализации целей занятия Вам необходимые такие исходные знания: 1. Прямые, посредственные, совокупные и совместные измерения. 2. Погрешности средств измерений. 3. Погрешности результатов измерений. 4. Инструментальные погрешности 5. Методические погрешности 6. Основная, дополнительная и эксплуатационная погрешности 7. Влияние помех на результат измерения. 8. Погрешности округления. 9. Погрешности отсчета. 10. Погрешности табличных данных.
5. Задача для проверки студентами своего исходного уровня знаний.
Контрольные вопросы
1. Что такое измерение. 2. Какие измерения зовут прямыми. 3. Какие измерения зовут посредственными. 4. Какие измерения зовут совокупными. 5. Какие измерения зовут совместными. 6. Какие средства измерений Вы знаете. 7. Какие погрешности результатов измерений Вы знаете. 8. Что такое инструментальные погрешности. 9. Что такое методические погрешности. 10. Что такое основная погрешность. 11. Что такое дополнительная погрешность. 12. Что такое эксплуатационная погрешность. 13. Погрешности округления. 14. Погрешности отсчета. 15. Погрешности табличных данных
6. Информацию для упрочения исходных знаний-умений можно найти в пособиях: 1 Жуматій П.Г. Лекция “Математическая статистика”. Одесса, 2009. 2 Жуматій П.Г. “ Обработка медико-биологических данных”. Одесса, 2009. 3 Чалый О.В., Агапов Б.Т., Цехмістер Я.В. Медицинская и биологическая физика. Киев, 2004. Содержание учебного материала из данной темы с выделением основных узловых вопросов. Основным образом получения информации есть измерения, то есть экспериментальное определение разных величин. В более широком смысле измерением называется операция, в результате которой мы познаем, в сколько раз величина, которая измерится, больше или меньше соответствующей величины, принятой чем единица. Результаты всех измерений, как бы тщательно и на каком бы научном уровне они не выполнялись, удерживают некоторые погрешности. Поэтому в задачу измерений входит не только определение величины, но и оценка допущенной при измерении погрешности.
В зависимости от образа получения результата бывают: * прямые измерения, при которых результаты находят непосредственно с помощью прибора (измерение температуры больного термометром, артериальной давки - сфигмотонометром и др.); * посредственные измерения, при которых результаты находят на основе прямых измерений величин, связанных с искомой величиной известной зависимостью в виде формул, графиков, таблиц и др. (например, сопротивление живой ткани вычисляют за формулой, подставляя у нее вимірені с помощью приборов значения силы тока и напряжения); * совокупные измерения, при которых результаты находят, решая системы уравнений, которые получают при подстановке в формулу комплектов результатов прямых измерений, соответствующих разным условиям измерений (например, употребляя закон Ома для определения ЕРС термоэлемента E,
видим, что только значение силы тока I и внешнего сопротивления R можно найти с помощью прямых измерений; выход в применении совокупных измерений, а именно, необходимо измерить силу тока I при двух разных значениях внешнего сопротивления R, и подставить в формулу закона Ома комплекты значений I, R, чтобы получить систему двух уравнений относительно двух неизвестных E и r
решая которую находят искомый ответ); • совместные (общие) измерения - одновременные (прямые или посредственные) измерение двух или больше величин с целью определения вида зависимости между ними (например, одновременные измерения освещенности и силы фототока с целью построения люкс-амперной характеристики фотоэлемента). Характер проявления и причины возникновения погрешностей весьма разные, в связи с чем различают несколько десятков их разновидностей. Рассмотрим основные: * погрешности результатов измерений - числа, которые указывают возможные границы неопределенности значений величин, которые измеряются; * погрешности средств измерений - определенные свойства приборов и измерительных установок, которые приводят к отклонению результата измерения от истинного значения величины, которое измерится. Исторически часть наименований разновидностей погрешностей закрепилась за погрешностями результатов измерений, другая - за погрешностями средств измерений, а некоторые применяются и до одних, и к вторым. Среди погрешностей средств измерений различают: * инструментальные (приборные или аппаратурные) погрешности - это те, которые принадлежат данному средства измерения, могут быть определенные при испытаниях и записанные в его паспорт; * методические погрешности - это те, которые связаны не с прибором, а с методом его применения или положенным в основу его разработки, и, итак, не могут быть указанные в паспорте прибора, (к ним относится, в частности, погрешность отсчета, возникающая при округлении показов при отсчета со шкалы прилада); * основные погрешности - это те, которые присущий данному средству измерения при нормальных условиях эксплуатации; * дополнительные погрешности - это те, какие присущий средству измерение при отклонении условий эксплуатации от нормальных, предусмотренных в паспорте; * эксплуатационные погрешности присущий средства измерения в реальных условиях эксплуатации, они составляются с основных и дополнительных.
В процессе измерения на измерительный прибор действуют разные факторы, один из которых - величину, которая измерится, прибор должен выделить на фоне всех других помех. В зависимости от характера действия помех на прибор различают: * систематические погрешности, которые вызываются помехами, действующими одинаково при повторении одних и тех же измерений; * прогрессирующие (дрейфу) погрешности, которые вызываются помехами, которые медленно и непередусмотренно меняются по времени; * случайные погрешности, которые вызываются помехами, действующими случайно при повторении одних и тех же измерений, * грубые погрешности, которые вызываются неучетом резкого изменения условий измерения, неисправностью средств измерений, просчетом экспериментатора и др. Границы основной погрешности, которая допускается при производстве средств измерений, регламентируются государственными стандартами и указываются в паспорте и на шкале прибора. Для этого используются: * абсолютная погрешность
где
* относительная погрешность Е
где Е - предельное значение частные абсолютной погрешности * приведенная погрешность
где Для приборов с равномерной или степеневою шкалой нормировочное значение равняется: * верхней границе диапазона измерений, если нулевая отметка находится на краю шкалы или вне нее; * ширине диапазона измерений, если нулевая отметка находится внутри шкалы. Часто в качестве характеристики границы, которая определяет гарантированные погрешности, используется класс точности М, что задается в паспорте и на шкале прибора обычно одним из чисел: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001. Класс точности в зависимости от условных обозначений может характеризовать разные виды погрешностей: * приведенную погрешность * относительную погрешность Е, если на шкале указано одно из значений класса точности, обведенное колом, например, надпись 0,2 в кругу на шкале отвечает Е = 0,2%; * относительную погрешность Е, если на шкале указанная пара значений класса точности в виде
Погрешности округления, отсчета и табличных данных Погрешности округлений возникают вследствие округления к определенному разряду точного или приближенного числа, которым может быть результат измерения. При округлении пользуются правилом: * последнюю значащую цифру не меняем, если первая из цифр, которые откидываются, меньше 5; * последнюю значащую цифру увеличиваем на 1, если первая из цифр, которые откидываются, равняется или больше 5. При этом погрешность округления не превышает половины единицы разряда последней значащей цифры округленного числа. Пример 1. Округлить к десяткам числа 235,7. Решение. Первая из цифр, которые откидываются, равняется 5, поэтому округленное число составляет 240. Последняя значащая цифра округленного числа 4 обозначает число десятков, поэтому половина единицы разряда последней значащей цифры округленного числа равняется 5. Результат округления вместе с погрешностью записывают в виде 240 ± 5. Погрешность отсчета возникает при округлении показаний средств измерений. Предельное значение погрешности отсчета равняется: * 0,5 цены деления шкалы, если округлить показание к значению, соответствующему ближайший метке шкалы; * 0,2 цены деления шкалы, если возможно оценить на глаз 0,1 или 0,2 цены деления шкалы. Мы рассмотрели предельные значения погрешностей. Любая погрешность округления внутри интервала
8. Задача для самостоятельной подготовки студентов.
8.1 Задача для самостоятельного изучения материала с темы.
8.1.1 Практическое вычисление погрешностей
Практическое вычисление погрешностей прямых измерений
Погрешности прямых измерений составляются из инструментальных погрешностей, случайных погрешностей и погрешностей отсчета. В зависимости от соотношения между ними накладываются условия на количество измерений и метод вычисления погрешности измерений: * если случайная погрешность значительно меньшая за инструментальную (повторение измерений дает одинаковые результаты), то измерение нужно осуществлять один раз, а полуширина надежного интервала
где * если случайная погрешность значительно превосходит инструментальную (повторение измерений дает результаты, которые отличаются), то измерение нужно осуществлять несколько раз, а полуширина надежного интервала при надежной вероятности исчисляется по формуле
где * если случайная и инструментальная погрешности сравнении за величиной (повторение измерений дает как результаты, которые сбегают, так и такие, что слабо отличаются), то измерение нужно осуществлять несколько раз, а полуширина надійого интервала исчисляется по формуле
при этом учитывается влияние всех трех погрешностей, поскольку погрешность отсчета есть в данном случае составляющей случайной погрешности. После окончания вычислений результат измерений и рассчитанное значение погрешности необходимо округлить, употребляя правила: * погрешность результата измерений указывается двумя значащими цифрами, если первая с них меньше 3, и одной значащей цифрой в других случаях; * результат измерения округляется к тому же десятичного разряда, которым заканчивается округленное значение абсолютной погрешности (полуширины надежного интервала * округления осуществляется в окончательном ответе, а все предыдущие вычисления проводят с одном-двумя лишними знаками. Окончательный ответ записывают в виде
Пример 2. Обработать результат измерения биопотенциала покоя Решение. В данном примере инструментальная погрешность значительно превосходит случайную (повторение измерений дает одинаковые результаты), поэтому измерение осуществлялось один раз и полуширину надежного интервала
Коэффициент Стьюдента для заданной надежной вероятности
Границу основной погрешности вольтметра
это граница основной погрешности вольтметра
Граница погрешности отсчета v (поскольку поділки мелкие) равняется половине цены деления z, то есть Все величины, входные в формулу для полуширины надежного интервала
Конечный ответ записывают в виде
В соответствии с требованиями государственного стандарта в ответе для абсолютная погрешность оставлена две значащие цифры, а числовое значение результата измерений заканчивается цифрой того же разряда, который и значение полуширины надежного интервала. Пример 3. При измерении вязкости крови вискозиметром ВК-4 длина столбика крови l в капилляре принимала такие значения (мм) 35, 40, 37, 43, 45. Обработать результаты измерения, считая, что надежная вероятность представляет = 95%. Решение. В данном примере случайная погрешность значительно превосходит инструментальную, поэтому измерение осуществлялись несколько раз, а полуширину надежного интервала
Коэффициент Стьюдента при данной надежной вероятности
Выборочное среднее
Полуширина надежного интервала
Конечный ответ имеет вид
В соответствии с требованиями государственного стандарта в ответе для абсолютной погрешности оставленная одна значащая цифра, а числовое значение результата измерений заканчивается цифрой того же разряда, который и значение абсолютной погрешности.
Практическое вычисление погрешностей посредственных измерений
Задача посредственных измерений - нахождение искомой величины U, которая является известной функцией одной или нескольких сменных Однако, задача обычно упрощается из-за того, что погрешности аргументов малые, а частичные производные функции
.......................................... Конечная цель - найти величину U, представивши ответ в виде
Точечную оценку
Погрешности посредственных измерений вычисляют за формулами: * абсолютная погрешность
• относительная погрешность E
Естественно, что вычисляют за формулами только одну из погрешностей, а именно, ту, которую высчитать проще. Другу погрешность определяют, используя формулу
Для разных частных случаев формулы для абсолютной и относительной погрешности упрощаются. Так, для алгеброичной суммы
удобнее первой вычислить абсолютную погрешность
а для приложений, частных, степеней и корней такие функции в общем случае могут быть представленные в виде
где
Пример 4. Определить сопротивление кожи человека, исходя из данных прямых измерений приложенного напряжения U
а также силы тока I, прошедшего через живу ткань,
Сопротивление кожи R определяется формулой
Решение. Точечная оценка сопротивления кожи равна
Формула относится к случаю, когда удобнее первой вычислять относительную погрешность
Абсолютная погрешность равняется
Результат посредственного измерения сопротивления кожи R представляет
Обработка результатов общих измерений
На практике самая необходимость измерений большинства величин вызывается именно тем, что они не остаются постоянными, а меняются при изменении других величин. В этом случае целью измерения является определения вида зависимости между величинами, которые измерятся. Основной помехой для определения вида зависимости между величинами, которые измерятся, есть случайный разброс исследовательских данных. * если случайный разброс сменных Х и Y почти отсутствующий (дифузність исходных данных имела), то график можно построить, проводя через эти точки плавную кривую; при этом одну или несколько точек, которые не попали на нее, нужно рассматривать как возможные промахи. * если диффузность исходных данных значительная, то для них обработки надо применять статистические методы.
Одним из простейших експрес-методов статистической обработки есть метод обведения контура плавных границ полосы рассеяния экспериментальных точек. Если при этом для сохранности плавности границ некоторые из точек приходится оставить вне контура, то их рассматривают как возможные промахи или аномально большие случайные отклонения. Форма обведенной контуром полосы рассеяния экспериментальных точек часто уже позволяет сделать вывод о характере зависимости между сменными Х и Y. Для указания этой зависимости необходимо провести на глаз осевую линию этого контура. Не смотря на простоту метода контуров, он позволяет быстро определить положение и форму искомой кривой и провести ее, учитывая расположение всех экспериментальных точек. При большой дифузності данных, когда метод контуров не дает ответа, может быть полезным метод медианных центров. Обведенное контуром поле точек делят на несколько равных частей (3 - 5) и в каждой из них находят медианный центр, то есть точку пересечения вертикальной и горизонтальной линий слева и дело, и выше и ниже от которых расположено равное число точек. Потом через медианные центры проводят плавную линию. При использовании метода медианних центров промахи исключать не надо, поскольку оценка положения центра с помощью медианы нечуткая к промахам. Для получения уравнения кривой, которая описывает зависимость между сменными Х и Y, обычно пользуются методом наименьших квадратов. Для этого избирают пригодную функцию
что зависит от некоторых параметров y = от всех экспериментальных значений
Для минимизации высчитывают частичные производные
приравнивают их нулю и решают полученную систему p уравнений относительно неизвестных Дата добавления: 2015-02-05 | Просмотры: 1202 | Нарушение авторских прав |
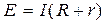 ,
,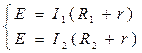 ,
,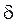 , которая выражается одним числом
, которая выражается одним числом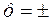 a,
a,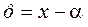 ;
;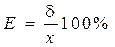 ,
,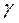
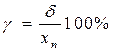 ,
,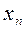 , выраженной в процентах.
, выраженной в процентах.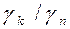 , при этом
, при этом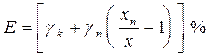 .
.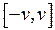 (v - предельное значение погрешности округления) имеет одну и ту же вероятность, поэтому полуширина надежного интервала
(v - предельное значение погрешности округления) имеет одну и ту же вероятность, поэтому полуширина надежного интервала 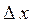 при надежной вероятности
при надежной вероятности 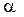 равняется
равняется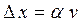 .
.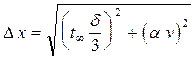 ,
,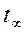 - коэффициент Стьюдента при n =
- коэффициент Стьюдента при n = 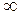 и надежной вероятности
и надежной вероятности 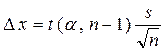 ,
,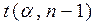 - коэффициент Стьюдента при заданных надежной вероятности
- коэффициент Стьюдента при заданных надежной вероятности 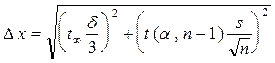 ,
,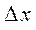 );
);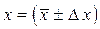 от.вим., Р =
от.вим., Р = 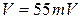 , выполненного с помощью вольтметра с ценой деления
, выполненного с помощью вольтметра с ценой деления 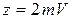 , границей измерений
, границей измерений 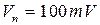 и классом точности
и классом точности 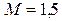 , считая, что надежная вероятность
, считая, что надежная вероятность 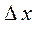 при надежной вероятности α нужно вычислять за формулой
при надежной вероятности α нужно вычислять за формулой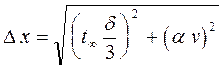 .
.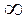 находим в таблице распределения Стьюдента
находим в таблице распределения Стьюдента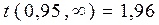 .
.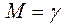 , а
, а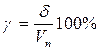 ,
,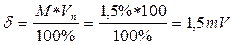 .
.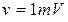 .
.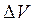 , найденные или известные из условий примера. Итак, имеем
, найденные или известные из условий примера. Итак, имеем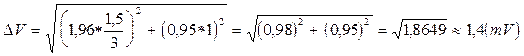 .
.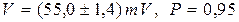 .
.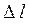 при надежной вероятности α надо вычислять за формулой
при надежной вероятности α надо вычислять за формулой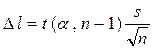 ,
,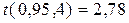 .
.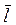 и выборочная оценка стандартного отклонения s результатов измерений от выборочного среднего вычисляются за известными формулами
и выборочная оценка стандартного отклонения s результатов измерений от выборочного среднего вычисляются за известными формулами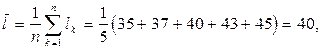
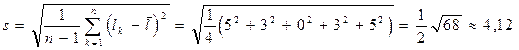 .
.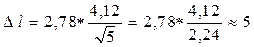 мм.
мм.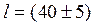 мм,
мм, 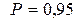 .
.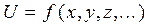 . В общем случае эта задача громоздкая. Нужно высчитать
. В общем случае эта задача громоздкая. Нужно высчитать 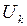 для каждого набора данных
для каждого набора данных 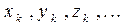
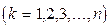 и дальше обрабатывать полученные значения
и дальше обрабатывать полученные значения 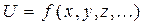 конечные. В этом случае необходимо заранее обработать результаты измерений сменных
конечные. В этом случае необходимо заранее обработать результаты измерений сменных 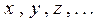 и представить их в стандартной форме
и представить их в стандартной форме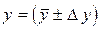 от.вим., Р =
от.вим., Р = 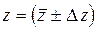 от.вим., Р =
от.вим., Р = 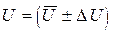 от.вим., Р =
от.вим., Р = 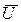 получают подстановкой выборочных средних
получают подстановкой выборочных средних 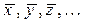 в формулу и необходимыми вычислениями
в формулу и необходимыми вычислениями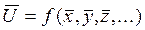 .
.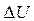 (полуширина надежного интервала)
(полуширина надежного интервала)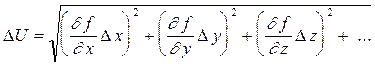
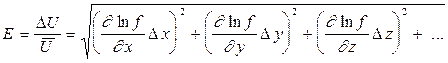 .
.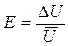 .
.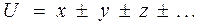
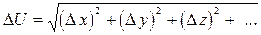 ,
,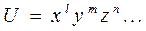 ,
,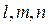 - любые действительные числа (положительные и отрицательные, целые и дроби) удобнее первой вычислять относительную погрешность
- любые действительные числа (положительные и отрицательные, целые и дроби) удобнее первой вычислять относительную погрешность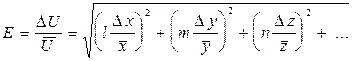 .
.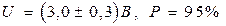 ,
,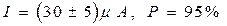 .
.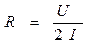 .
.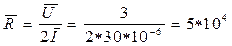 (ом).
(ом).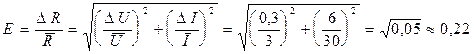 .
.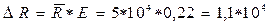 (ом).
(ом).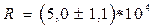 (ом),
(ом), 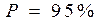 .
.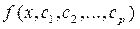 ,
,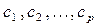 , которые подбирают так, чтобы сумма квадратов отклонений
, которые подбирают так, чтобы сумма квадратов отклонений 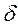 приближенной зависимости
приближенной зависимости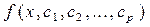
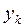 была минимальной
была минимальной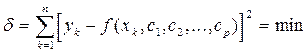 .
.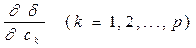 ,
,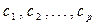 .
.