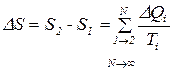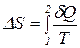АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Теоретическая часть. Понятие энтропии введено в термодинамику немецким физиком Р.Клаузиусом в 1865 г

Понятие энтропии введено в термодинамику немецким физиком Р.Клаузиусом в 1865 г. Слово "энтропия" в переводе с греческого означает "превращение". В данном случае имеется в виду превращение тепловой энергии в механическую и наоборот. Прежде чем дать определение и выяснить физический смысл энтропии, введем ряд понятий, касающихся тепловых процессов.

Состояние системы определяется набором параметров. Например, для заданной массы идеального газа таковыми являются давление Р, объем V и температура Т.

При изменении хотя бы одного из параметров говорят о процессе. Обратимым процессом называется такой процесс, который может происходить как в прямом, так и обратном направлениях, причем, если система вернулась в исходное состояние, то ни в ней, ни в окружающей среде не остается ни каких изменений.

Состояние системы называется равновесным, если во всех ее частях одинаковы температура, давление, концентрация молекул (если речь идет о газе) и т.д.

Процесс является обратимым, если в любой момент времени состояние системы является равновесным. Идеальные процессы: изотермический, изобарический, изохорический, адиабатный - обратимы.

Реальные тепловые процессы необратимы и только при определенных условиях их можно рассматривать как обратимые с той или иной степенью точности.

Циклом называется такая последовательность процессов, по завершении которых система возвращается в исходное состояние.

Особую роль в термодинамике играют функции состояния. Это такие функции, значение которых определяется только параметрами системы в данном состоянии и не зависит от предыстории, т.е. от того, в результате каких изменений система пришла в это состояние. Примером функции состояния может служить внутренняя энергия идеального одноатомного газа

,

где m - масса, M - молярная масса, R - универсальная газовая постоянная, Т - абсолютная температура.

Функция состояния после каждого цикла принимает одно и то же значение. Более того, при переходе системы из любого состояния (1) в любое состояние (2) изменение функции состояния (∆f = f₂-f₁) не зависит от выбора пути перехода системы из (1) в (2).

Пусть ∆Q сколь угодно малое количество теплоты, получаемое системой. Тогда количество теплоты, полученное системой за один цикл, можно представить в виде суммы

,

где считаем ∆Q_i> 0, если система получает тепло, и ∆Q_i< 0, если система отдает тепло. Другими словами, мы представили весь цикл в виде последовательности большего числа N (N→∞) процессов, в каждом из которых система либо получает, либо отдает тепло. В термодинамике показывается, что в цикле Карно, состоящего из двух изотерм и двух адиабат,

,

и следовательно, Q не является функцией состояния системы. В частности, при

Рис. 6.1

переходе системы из состояния (1) в состояние (2) в общем случае и зависит от выбора процесса (см. рис.6.1). То же самое относится к работе, совершаемой системой при таком переходе.

Оказалось, однако, что, если вместо ∆Q_i взять отношение ∆Q_i/Т_i, где Т_i - температура системы, при которой происходит данный теплообмен, то за цикл

.

Именно это и было впервые показано Р.Клаузиусом. Следовательно, величину ∆Q_i/Т_i (ее называют приведенной теплотой) можно рассматривать как изменение некоторой функции состояния - S (ее и назвали энтропией). В частности, при переходе системы из состояния (1) в состояние (2) изменение энтропии

или в пределе

не зависит от выбора пути. Знаком δQ обозначено то, что количество теплоты не является полным дифференциалом.

Второе начало термодинамики, используя понятие энтропии, формулируется следующим образом:

В замкнутой системе возможны лишь такие процессы, при которых энтропия не будет убывать, т.е. ∆S ≥ 0, где знак " = " относится к обратимым, а знак " > " - к необратимым процессам.

Если первое начало термодинамики говорит только о количественных соотношениях при превращении энергии из одного вида в другой, то второе начало характеризует направленность эволюции состояния системы. Оно определяет, какие процессы могут происходить в данной системе, а какие невозможны.

С молекулярно-кинетических представлений энтропию можно характеризовать как меру неупорядоченности частиц системы. Так, например, при уменьшении объема газа его молекулы вынуждены занимать все более определенные положения одна относительно другой, что соответствует большему порядку в системе. При этом энтропия убывает. Когда газ конденсируется в жидкость или жидкость кристаллизуется при постоянной температуре, выделяется теплота, энтропия убывает. И в этом случае происходит изменение порядка расположения частиц.

Неупорядоченность системы качественно характеризуется термодинамической вероятностью W_тер (число способов размещения частиц, или число микросостояний, реализующих данное макросостояние, Больцман установил связь энтропии S_u термодинамической вероятностью W_тер

S = k lnW_тер,

где k - постоянная Больцмана.

В системе СИ энтропия измеряется в Дж/К.

Дата добавления: 2015-11-26 | Просмотры: 415 | Нарушение авторских прав