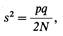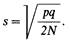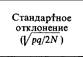АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 3. Пер. с англ.: – М.: Мир, 1988. – 336 с.

Прочитайте:
  1. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  2. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  3. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  4. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  5. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  6. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  7. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  8. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  9. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  10. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.

126 Эволюция генетического материала

нах, полученных от выросших растений, будет очень близка к 1/2, хотя может оказаться и чуть больше, и чуть меньше.

Если известно число родителей в исходном поколении и частоты аллелей в нем, как это было в только что приведенном примере, то мы можем рассчитать вероятность получить в следующем поколении те или иные частоты аллелей. Для этого нам нужно знать вариансу, или дисперсию, частот аллелей в следующем поколении. Варианса служит мерой изменчивости, обнаруживаемой при сравнении различных выборок (см. приложение 3). Если имеются два аллеля с частотами p и q, причем число родителей равно N (так что число генов в исходном поколении равно 2N) то варианса (s2)частоты аллеля в следующем поколении составляет

а стандартное отклонение может быть выражено как

Эти формулы отражают обратную зависимость между величиной выборки 2N и теоретически ожидаемой изменчивостью частот аллелей. Табл. 23.6 иллюстрирует эффект дрейфа генов от одного поколения к другому в двух случаях: 1) когда p = q = 0,5 и 2) когда p = 0,3, a q = = 0,7. Для каждого случая рассматриваются три варианта эффективной численности популяции: N = 5, 50 и 500. Реально наблюдаемая частота аллеля p укладывается в интервал p ± 2 стандартных отклонений с 95% вероятностью. В малых популяциях с эффективной численностью 5 особей этот интервал ожидаемых значений p в следующем поколении лежит между 0,18 и 0,82; чем больше численность популяции, тем уже интервал ожидаемых значений частоты аллеля в следующем поколении. Заметим, что ширина этого интервала убывает с ростом эффективной численности популяции как корень квадратный из отношения эффективной численности одной популяции к эффективной численности другой.

 

Таблица 23.6. Эффект случайного дрейфа генов из одного поколения в другое
Численность популяции (N) Число гамет (2 N) Варианса (pq/2N)
Случай 1        
p= q = 0,5        
    0,025 0,16 0,18-0,82
    0,0025 0,05 0,40-0,60
    0,00025 0,016 0,468-0,532
Случай 2        
p = 0,3; q = 0,7        
    0,021 0,145 0,01-0,59
    0,0021 0,046 0,208-0,392
    0,00021 0,0145 0,271-0,329

Дата добавления: 2015-12-16 | Просмотры: 361 | Нарушение авторских прав

При использовании материала ссылка на сайт medlec.org обязательна! (0.003 сек.)