 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
ДИНАМИЧЕСКИЕ РЯДЫПри изучении динамики какого-либо явления прибегают к построению динамического ряда. Динамический ряд - это ряд однородных статистических величин, показывающих изменение какого-либо явления во времени и расположенных в хронологическом порядке через определенные промежутки времени. Числа, составляющие динамический ряд, называются уровнями. У ровень ряда - размер (величина) того или иного явления, достигнутый в определенный период или к определенному моменту времени. Уровни ряда могут быть представлены абсолютными, относительными или средними величинами. Динамические ряды делятся на простые (состоящие из абсолютных величин) и сложные (состоящие из относительных или средних величин). Простые динамические ряды могут быть моментными и интервальными. Моментный динамический ряд состоит из величин, характеризующих явление на какой-то определенный момент (дату). Примером могут служить статистические сведения, обычно регистрируемые на начало или конец месяца, квартала, года (численность населения на начало года, число врачей, средних медицинских работников на конец года, число лечебных учреждений, коек на конец года и т.д.). Интерв а льный динамический ряд состоит из чисел, характеризующих явление за определенный промежуток времени (интервал) - за неделю, месяц, квартал, год и т. д. Примером такого ряда могут служить данные о числе родившихся, умерших за год, число инфекционных заболеваний за месяц и т. д. Особенностью интервального ряда является то, что его члены можно суммировать (при этом укрупняется интервал), или дробить. Например, имея данные о количестве заболевших дизентерией, зарегистрированных за каждые день, можно построить динамический ряд с интервалом в неделю, месяц, год. Динамические ряды могут подвергаться преобразованиям, целью которых является выявление особенностей изменения изучаемого процесса, а также достижение наглядности. Прежде всего ряд может быть охарактеризован самими величинами членов ряда, называемыми уровнями. Величина первого члена ряда носит название начального (исходного) уровня, величина последнего члена ряда - конечного уровня. Средняя величина из всех членов ряда называется средним уровнем. Абсолютный прирост (убыль) - величина разности между последующим и предыдущим уровнями; прирост выражается числами с положительным знаком, убыль - с отрицательным знаком. Значение прироста или убыли отражают изменения уровней динамического ряда за определенный промежуток времени. Темп рост а (снижения) - показывает отношение каждого последующего уровня к предыдущему уровню и обычно выражается в процентах. Темп прирост а (убыли) - отношение абсолютного прироста или убыли каждого последующего члена ряда к уровню предыдущего, выраженное в процентах. Темп прироста может быть вычислен также по формуле: Темп роста - 100% Абсолютное значение одного процента приро с та (убыли) - получается от деления абсолютной величины прироста или убыли на показатель темпа прироста или убыли за тот же период. Для более наглядного выражения нарастания или убывания ряда можно преобразовать его путем вычисления показателей наглядности, показывающих отношение каждого члена ряда к одному из них, принятому за сто процентов. Примеры расчета показателей динамического ряда представлены в таблице 10. Таблица 10 Младенческая смертность в Индии в 1992-1995гг. (на 1000)
Абсолютный прирост (убыль): 1993: 98.0 - 95.0 = + 3.0 1994: 96.0 - 98.0 = - 2.0 1995: 87.9 - 96.0 = - 8.1 Темп роста (убыли):
Темп прироста (убыли):
Показатель наглядности: 1992: = 100%;
Иногда динамика изучаемого явления представлена не в виде непрерывно меняющегося уровня, а отдельными скачкообразными изменениями. В этом случае для выявления основной тенденции в развитии изучаемого явления прибегают к выравниванию д инамического ряда. При этом могут быть использованы следующие приемы: укрупнение интервала, вычисление групповой средней, вычисление скользящей средней, выравнивание методом наименьших квадратов. Укрупнение интервала производят путем суммирования данных за ряд смежных периодов. В результате получаются итоги за более продолжительные промежутки времени. Этим сглаживаются случайные колебания и более четко определяется характер динамики явления. Вычисление групповой средней заключается в определении средней величины каждого укрупненного периода. Для этого необходимо суммировать смежные уровни соседних периодов, а затем сумму разделить на число слагаемых. Этим достигается большая ясность изменений во времени. Вычисление скользящей средней в некоторой степени устраняет влияние случайных колебаний на уровни динамического ряда и более заметно отражает тенденцию явления. При ее вычислении каждый уровень ряда заменяется на среднюю величину из данного уровня и двух соседних с ним. Чаще всего суммируются последовательно три члена ряда, но можно брать и больше Пример выравнивания динамического ряда данных о заболеваемости дизентерией по месяцам года представлен в таблице 11. Таблица 11. Число заболеваний дизентерией по месяцам года
Увеличивая в данном динамическом ряду интервал до 3 месяцев получаем число заболевших за квартал (графа 3, табл.11). Полученные данные указывают на постепенное возрастание числа заболевших дизентерией и его максимум в 3 квартале, после чего заболеваемость снижается. Разделив каждую полученную сумму на 3 (число месяцев в квартале), получаем средние величины по группам, отражающие ту же закономерность (графа 4. табл.11). Скользящая средняя обычно вычисляется как средня арифметическая из 3 смежных уровней (данного, предыдущего и последующего). Для первого и последнего уровней скользящая средняя не рассчитывается (графа 5, табл.11). Для 2-го уровня: Метод наименьших квадратов - один из наиболее точных способов выравнивания динамического ряда. Этот метод преследует цель устранить влияние временно действующих причин, случайных факторов и выявить основную тенденцию в динамике явления, вызванную воздействием только длительно действующих факторов. Выравнивание производится по линии, наиболее соответствующей характеру динамики изучаемого явления, при наличии основной тенденции к росту или снижению частоты явления. Такой линией является обычно прямая, которая наиболее точно характеризует основное направление изменений. Этот метод позволяет дать количественную оценку выявленной тенденции и на этой основе рассчитать прогнозируемые уровни на следующий год. Дата добавления: 2015-02-06 | Просмотры: 1579 | Нарушение авторских прав |
 ;
; 
 ;
;  ;
; 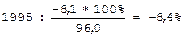
 ;
; 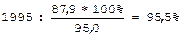
 = 2, 7; для 3-го уровня:
= 2, 7; для 3-го уровня:  = 3.7 и т. д.
= 3.7 и т. д.