 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Оценка достоверности статистических величинВ статистике выделяют два основных метода исследования - сплошной и выборочный. При сплошном методе объектом исследования является вся совокупность единиц, представляющих изучаемое явление, которая называется генеральной совокупностью. Однако, поскольку сплошное исследование является трудоемким и дорогостоящим, при проведении медико-биологических статистических исследований чаше всего используется выборочный метод. При этом исследование проводится на выборочной совокупности, являющейся частью генеральной совокупности, отобранной для обследования и изучения. При проведении выборочного исследования обязательным является соблюдение следующих требований: 1) репрезентативность выборочной совокупности; 2) достаточное число единиц наблюдений выборочной совокупности. Для соблюдения первого требования, репрезентативности, очень важен способ отбора части единиц наблюдений из генеральной совокупности. Статистикой выработан ряд способов осуществления выборки. 1. Случайный отбор, основу которого составляет отбор единиц наблюдений путем жеребьевки. При этом для каждой единицы обеспечивается равная возможность попасть в выборку. 2. Механический отбор, при котором единицы генеральной совокупности последовательно расположенные по какому-либо признаку (по алфавиту, по датам обращения к врачу и т.д.), механически разбиваются на равные части. Из каждой части в заранее обусловленном порядке отбирают каждую пятую, десятую или какую-либо иную единицу наблюдения таким образом, чтобы обеспечить необходимый объем выборки. 3. Типический (типологический) отбор предполагает обязательное предварительное расчленение генеральной совокупности на отдельные качественно однородные группы (типы). Выборка, произведенная в случайном порядке в каждой из установленных типических групп, и будет называться типической. 4. Серийный (гнездный) отбор предполагает выборку из генеральной совокупности не отдельных единиц, а целых серий групп единиц, которые отбираются по принципам случайного или механического отбора. Серийный отбор очень удобен в практическом отношении, хотя точность его результатов уступает другим методам отбора. При выборе единиц наблюдения любым из перечисленных способов, возможны ошибки смещения, т.е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки. Такие ошибки носят название случайных ошибок р е пр ез ентативно с ти (m), и являются Фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности. На практике для определения средней ошибки выборки при проведении статистических исследований, используются следующие Формулы: 1) для расчета ошибки репрезентативности (mм) средней арифметической величины (М):
n - численность выборки.
2) для расчета ошибки репрезентативности (mР) относительной величины (Р):
q - 100 - Ρ; n - численность выборки. В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, число наблюдений уменьшается на единицу, т.е.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7% Определенной степени вероятности безошибочного прогноза соответствует определенная величина предельной ошибки случайной выборки (Δ) Определяется эта величина по формуле: Δ=t * m, где t - доверительный коэффициент, который при вероятности безошибочного прогноза 95% равен 2. при вероятности безошибочного прогноза 99% - 3,. и при вероятности безошибочного прогноза 99,7% - 3,3. Используя предельную ошибку выборки (Δ), можно определить доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, характеризующей всю генеральную совокупность (средней или относительной). Для определения доверительных границ используются следующие Формулы: 1) для средних величин:
t - доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM - ошибка репрезентативности средней величины. 2) для относительных величин:
t - доверительный коэффициент; mP - ошибка репрезентативности относительной величины. При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента (см. Табл.6). Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, указывающей на имеющееся число степеней свободы (n`), которое равно n-1. Таблица 6. Таблица значений критерия t (Стьюдента)
При проведении выборочного медико-биологического статистического исследования важное значение имеет определение необходимого числа наблюдений (n). Число наблюдений при проведении выборочного исследования зависит от вероятности безошибочного прогноза результатов исследования (определяется по коэффициенту t), а также от конкретных особенностей организации исследования и объекта наблюдения. При проведении медико-биологических статистических исследований для определения минимально допустимого числа наблюдений используются следующие формулы: 1) для средних величин:
2) для относительных величин:
Величина Δ определяется исследователем на основании необходимой вероятности безошибочного прогноза. Среднее квадратическое отклонение (σ) и относительная величина (Р) определяются либо на основании ранее проведенных исследований, либо на основании имеющихся данных литературы. Дата добавления: 2015-02-06 | Просмотры: 994 | Нарушение авторских прав |

 , где σ - среднее квадратическое отклонение;
, где σ - среднее квадратическое отклонение;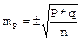 , где Ρ - соответствующая относительная величина (рассчитанная, например, в процентах (%));
, где Ρ - соответствующая относительная величина (рассчитанная, например, в процентах (%)); ,где
,где  - доверительные границы средней величины в генеральной совокупности;
- доверительные границы средней величины в генеральной совокупности;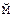 - средняя величина, полученная при проведении исследования на выборочной совокупности;
- средняя величина, полученная при проведении исследования на выборочной совокупности;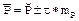 , где
, где 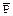 - доверительные границы относительной величины в генеральной совокупности;
- доверительные границы относительной величины в генеральной совокупности; - относительная величина, полученная при проведении исследования на выборочной совокупности;
- относительная величина, полученная при проведении исследования на выборочной совокупности; n
n