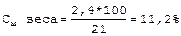АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Среднее квадратическое отклонение

Приближенный метод оценки колеблемости вариационного ряда - это определение лимита, т.е. минимального и максимального значе­ния количественного признака, и амплитуды - т.е. разности между наибольшим и наименьшим значением вариант (Vmax - Vmin). Одна­ко лимит и амплитуда не учитывают значений вариант внутри ряда.

Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ - сигма).

Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Так, например, при изучении средней длительности лечения больных в двух больницах были получены следующие результаты:

Средняя длительность лечения в обеих больницах одинакова, од­нако во второй больнице колебания были значительнее.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой
(V-M=d). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю (графа 3. табл. 5).

3. Возводят каждое отклонение в квадрат (графа 4. табл. 5).

4. Перемножают квадраты отклонений на соответствующие частоты d²*p (графа 5, табл. 5).

5. Вычисляют среднее квадратическое отклонение по формуле:

при n больше 30,или . при n меньше либо равно 30, где n - число всех вариант

Методика расчета среднего квадратического отклонения приведе­на в таблице 5.

Среднее квадратическое отклонение позволяет установить сте­пень типичности средней, пределы рассеяния ряда, сравнить колеб­лемость нескольких рядов распределения. Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Таблица 5

М=20 n=95 Σ=252

Коэффициент вариации вычисляется по формуле:

Пример: по данным специального исследования средний рост мальчиков 7 лет в городе N составил 117.7 см (σ=5. 1 см), а сред­ний вес - 21,7 кг (σ=2,4 кг). Оценить колеблемость роста и веса путем сравнения средних квадратических отклонений нельзя, т. к. вес и рост - величины именованные. Поэтому используется относи­тельная величина - коэффициент вариации:

,

Сравнение коэффициентов вариации роста (4.3%) и веса (11.2%) показывает, что вес имеет более высокий коэффициент вариации,следовательно,является менее устойчивым признаком.

Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

Средние величины широко применяются в повседневной работе ме­дицинских работников. Они используются для характеристики Физи­ческого развития, основных антропометрических признаков: рост, вес. окружность груди, динамометрия и т.д. Средние величины при­меняются для оценки состояния больного путем анализа физиологи­ческих, биохимических сдвигов в организме: уровня артериального давления, частоты сердечных сокращений. температуры тела, уровня биохимических показателей, содержания гормонов и т. д. Широкое применение средние величины нашли при анализе деятельности лечеб­но-профилактических учреждений, например: при анализе работы ста­ционаров вычисляются показатели среднегодовой занятости койки, средней длительности пребывания больного на койке и т. д.

Дата добавления: 2015-02-06 | Просмотры: 1268 | Нарушение авторских прав