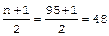|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Виды средних величинВ медицинской практике наиболее часто используются следующие средние величины: мода, медиана, средняя арифметическая. Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определении среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей) и другие. Мода (Mo) - величина признака, чаще других встречающаяся в совокупности. За моду принимают варианту, которой соответствует наибольшее количество частот вариационного ряда. Медиана (Me) - величина признака, занимающая срединное значение в вариационном ряду. Она делит вариационный ряд на две равные, части. На величину моды и медианы не оказывают влияния числовые значения крайних вариант, имеющихся в вариационном ряду. Они не всегда могут точно характеризовать вариационный ряд и применяются в медицинской статистике относительно редко. Более точно характеризует вариационный ряд средняя арифметическая величина. С редняя арифметическая (М, или В простом вариационном ряду, где варианты встречаются только по одному разу, вычисляется средняя арифметическая простая по формуле:
n - число наблюдений, Σ - знак суммы В обычном вариационном ряду вычисляется средняя арифметическая взвешенная по формуле:
Ρ - частота встречаемости вариант. n - число наблюдений. S - знак суммы
Пример расчета средней арифметической взвешенной приведен в таблице 4. Таблица 4 Определение средней длительности лечения больных в специализированном отделении больницы
n=95 S=1900,
В приведенном примере модой является варианта, равная 20 дням, поскольку она повторяется чаще других - 29 раз. Мо = 20. Порядковый номер медианы определяется по формуле: Место медианы приходится на 48-ю варианту, числовое значение которой равно 20. Средняя арифметическая, рассчитанная по формуле, равна также 20. Средние величины являются важными обобщающими характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака. Если вариационный ряд более компактен, менее рассеян и все отдельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариационный ряд растянут, отдельные значения значительно отклоняются от средней, т.е. имеется большая вариабельность количественного признака, то средняя менее типична, хуже отражает в целом весь ряд. Одинаковые по величине средние могут быть получены из рядов с различной степенью рассеяния. Так, например, средняя длительность лечения больных в специализированной отделении больницы также будет равна 20, если все 95 больных находились на стационарном лечении по 20 дней. Обе вычисленные средние равны между собой, но получены из рядов с разной степенью колеблемости вариант. Следовательно, для характеристики вариационного ряда, помимо средней величины, необходима другая характеристика, позволяющая оценить степень его колеблемости. Дата добавления: 2015-02-06 | Просмотры: 803 | Нарушение авторских прав |
 ) - рассчитывается на основе всех числовых значений изучаемого признака.
) - рассчитывается на основе всех числовых значений изучаемого признака. , где V - числовые значения вариант,
, где V - числовые значения вариант,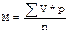 , где V - числовые значения вариант.
, где V - числовые значения вариант.