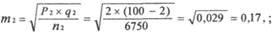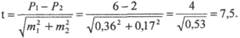|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Определение доверительных границ средних и относительных величинЗнание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно при проведении медико-биологических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7% или 99,9%. Определенной степени вероятности безошибочного прогноза соответствует определенная величина предельной ошибки случайной выборки (А — дельта). Определяется эта величина по формуле: Δ = t х т, где t— доверительный коэффициент, соответствующий определенной степени вероятности безошибочного прогноза. Доверительный коэффициент имеет определенные значения: для большой выборки (л > 30) при вероятности безошибочного прогноза 95,5% t равен 2, при вероятности безошибочного прогноза 99% — 2,6 и при вероятности безошибочного прогноза 99,7% — 3,0, при вероятности безошибочного прогноза 99,9% — 3,3. Для малой выборки (л < 30) его значения определяются по специальной таблице значений / Стьюдента. Используя предельную ошибку выборки (Δ), можно определить доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины (средней или относительной), характеризующей всю генеральную совокупность. Другими словами, доверительные границы — это крайние значения возможных отклонений, в пределах которых может колебаться искомая величина (относительная или средняя) в генеральной совокупности. Для определения доверительных границ используются следующие формулы: 1) для средних величин: Мген = Мвыб. ± t х тм, где Мген — доверительные границы средней величины в генеральной совокупности; Мвыб.. — средняя величина, полученная при проведении исследования на выборочной совокупности; t — доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; тм — ошибка репрезентативности средней величины. 2) для относительных величин:P ген = P выб ± t х тр, где Лен. — доверительные границы относительной величины в генеральной совокупности; Рвыб. — относительная величина, полученная при проведении исследования на выборочной совокупности; t — доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; тр — ошибка репрезентативности относительной величины. Пример 12: при испытании нового лечебного препарата на группе больных 75 человек положительный эффект {Р) был отмечен у 82% пациентов (ошибка репрезентативности т = ± 3%). С вероятностью безошибочного прогноза 95,5% можно утверждать, что при применении этого препарата у всех больных положительный эффект наблюдался бы с частотой от 76 до 88% (Р±2т). Доверительные границы показывают также, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера. В нашем примере мы можем полагать с достоверностью 95,5%. что при повторных исследованиях положительный эффект будет колебаться от 76 до 88%. При малом числе наблюдений (л < 30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента (см. приложение 1). Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, указывающей на имеющееся число степеней свободы (n'),которое равно n-1. Пример 13: при использовании нового метода лечения на группе больных (19 человек) получены следующие данные: средняя длительность лечения (M) составила 11 дней, средняя ошибка (т) = ± 1,5 дня. 1. Определяем число степеней свободы: л' = я - 1 = 19-1 = 18. 2. По таблице Стьюдента (приложение 1) находим значение t: при вероятности ошибки не более 5% и я' = 18 значение t равно 2,1. Вывод: с достоверностью 95,5% можно утверждать, что при изучении генеральной совокупности величина средней длительности лечения будет колебаться в пределах 11 ± 2 х 2,1 дней, то есть от 6,8 до 15,2 дней. Оценка достоверности разности относительных и средних величин При проведении медико-биологических исследований на двух сравниваемых совокупностях возникает необходимость определить не только их различие, но и его достоверность. Например, при сравнении результатов исследования в контрольной и экспериментальной группах, уровней летальности в двух больницах, показателей заболеваемости за два года и т. д. Метод оценки достоверности разности показателей или средних величин позволяет установить, существенны ли выявленные различия, или они являются результатом действия случайных причин. В основе метода лежит определение критерия достоверности (/), который рассчитывается по специальным формулам для средних и относительных величин. Формула расчета критерий достоверности (t) разности: для средних величин:
для относительных величин:
где M1 и М2, P1 и Р2 — статистические величины, полученные при проведении выборочных исследований; т1 и т2 — их ошибки репрезентативности; / — коэффициент достоверности. При изучении явления на б ольшой выборке разность достоверна при t > 2, что соответствует вероятности безошибочного прогноза 95,5% (при и>30). При t > 3 различия между сравниваемыми величинами достоверны с вероятностью безошибочного прогноза 99,7%. В большинстве медицинских исследований достаточно иметь значение t, равное или более 1,96. Тогда выявленные различия достоверны, не случайны, статистически подтверждены с вероятностью безошибочного прогноза равной или более 95%. При величине коэффициента достоверности t < 1,96 степень вероятности безошибочного прогноза менее 95%. При такой степени вероятности безошибочного прогноза разность сравниваемых показателей недостоверна. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений. Если после увеличения численности выборки, и, соответственно, уменьшения ошибки репрезентативности, различие продолжает оставаться недостоверным, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку. В качестве примера 14 сопоставим уровни общей летальности в двух больницах (табл. 8): Таблица 8 Летальность в двух больницах за 200.. год
а) рассчитываем
б) вычисляем критерий достоверности t:
Рассчитанный критерий достоверности t равен 7,5, что указывает на достоверную разницу уровней летальности в сравниваемых больницах с вероятностью безошибочного прогноза более 99,9% (приложение 1). Для определения достоверности различий между двумя показателями или средними величинами при малом числе наблюдений (и < 30, в каждой группе) критерий достоверности оценивается по таблице значений критерия / Стьюден-та по числу степеней свободы (и'). При этом число степеней свободы определяется, как сумма чисел наблюдений в каждой группе без двух (n' =n1 + n2 - 2). Метод оценки достоверности показателей и средних величин широко используется при проведении клинико-статистических исследованиях, при сравнительном анализе данных об эффективности различных методов диагностики и лечения. Он необходим при сравнении данных в динамике, по отделениям, участкам, контингентам больных и т. д. Применение этого метода целесообразно при оценке различий в уровнях заболеваемости, смертности, летальности, средней длительности лечения, частоты послеоперационных осложнений, эффективности диспансеризации и других интенсивных показателей и средних величин. Этот метод оценки достоверности не рекомендуется применять при анализе показателей распределения (экстенсивных показателей, показателей удельного веса), т.к. величина их зависит от соотношения составных частей внутри совокупностей и сделать вывод о наличии или отсутствии различий на основании экстенсивных показателей нельзя. Метод оценки достоверности по /-критерию (метод Стьюдента) применяют при сравнении двух величин. Если необходимо сравнить большее количество объектов, групп наблюдения, применяют другие методы. Дата добавления: 2015-02-06 | Просмотры: 2905 | Нарушение авторских прав |
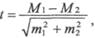
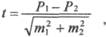
 средние ошибки показателей летальности (Р\ и Р2):
средние ошибки показателей летальности (Р\ и Р2):