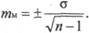АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Определение ошибки репрезентативности при малой выборке

В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, число наблюдений уменьшается на единицу.

Ошибка средней величины при малом числе наблюдений определяется по формуле:

Ошибка относительного показателя при малом числе наблюдений опре­деляется по формуле:

Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Однако для получения досто­верных показателей нельзя беспредельно увеличивать число наблюдений. К тому же, конкретные материалы нередко ограничены по численности изучае­мой совокупности. Для оценки достоверности выборочного показателя (сред­ней арифметической величины) принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку; в этом случае по­казатель (или средняя арифметическая величина) считается достоверной.

Пример 11: средняя длительность лечения больных с язвенной болезнью желудка М= 18,5 дней, среднее квадратическое отклонение σ = ±2,4 дня, чис­ленность выборки л = 64 человек. Ошибка средней арифметической величины т = ± 0,3. Средняя величина превышает свою утроенную ошибку. Следователь­но, можно считать полученный результат достоверным.

Дата добавления: 2015-02-06 | Просмотры: 696 | Нарушение авторских прав