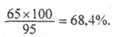АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

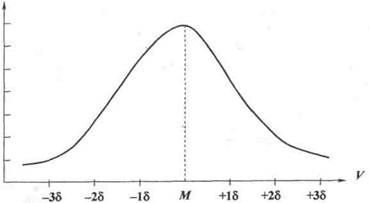
Значение среднего квадратического отклонения

1. Среднее квадратическое отклонение характеризует разброс вариант
относительно средней величины, т. е. характеризует колеблемость вариацион­
ного ряда.

Чем больше среднее квадратическое отклонение, тем степень разнообра­зия данного ряда выше.

2. Среднее квадратическое отклонение используется для сравнительной
оценки степени соответствия средней арифметической величины тому вариа­
ционному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распреде­ления. Кривая, отображающая это распределение, имеет вид плавной колоколо-образной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значе­ниями средйей арифметической и среднего квадратического отклонения суще­ствует строгая математическая зависимость. Теоретическое распределение ва­риант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить зна­чения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней ариф­метической равномерно располагаются варианты с большими и меньшими зна­чениями (рис. 1).

Установлено, что при нормальном распределении признака:

- 68,3% значений вариант находится в пределах М± 1σ;

- 95,5% значений вариант находится в пределах М± 2σ;

- 99,7% значений вариант находится в пределах А/± Зσ.

Если к средней арифметической величине прибавить или отнять одну сигму (M± 1σ), то при нормальном распределении признака в статистической совокупности в этих границах будет находиться не менее 68,3% всех вариант. В пределах М± 2σ будет заключено 95,5% всех наблюдений. Если к средней при­бавить или отнять три сигмы (М± Зσ), то в этих границах будут расположены 99,7% всех вариант изучаемой совокупности.

В нашем примере (табл.7) М = 20 дней, σ = 1,6 дня. В пределах М±1σ находится 65 вариант, что составляет 68,4% всех наблюдений

Такое распределение вариант позволяет считать, что данный вариационный ряд является однородным, а средняя арифметическая величина — типичной.

3. Среднее квадратическое отклонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М ± 1σ обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1с указыва­ет на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрической практике для индивидуальной оценки уровня физического развития детей (метод сиг-мальных отклонений), для разработки стандартов детской одежды, обуви, школьной мебели и т. д.

5. Среднее квадратическое отклонение необходимо для характеристики
степени разнообразия изучаемого признака и вычисления ошибки средней
арифметической величины.

Дата добавления: 2015-02-06 | Просмотры: 1122 | Нарушение авторских прав