 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Средние величиныЕдиницы наблюдения статистической совокупности могут характеризоваться количественными признаками. Каждый изучаемый количественный признак принимает разные значения у различных единиц статистической совокупности, он меняется в своем значении от одной единицы совокупности к другой. Это различие между единицами совокупности называется вариациями. Числовое значение признака для той или иной единицы совокупности называют вариантой и обозначают буквой V или X. Для анализа количественных признаков рассчитывают средние величины. Средние величины дают обобщающую характеристику статистической совокупности по определенному изменяющемуся количественному признаку. Средняя величина характеризует весь ряд наблюдений одним числом, выражающим общую меру изучаемого признака. Она нивелирует случайные отклонения отдельных наблюдений и дает типичную характеристику количественного признака. Важнейшим условием при вычислении средних величин является качественная однородность совокупности, для которой они рассчитываются. Только в этом случае она будет объективно отображать характерные особенности изучаемого явления. Второе требование заключается в том, что средняя величина только тогда выражает типичные размеры признака, когда она основывается на массовом обобщении изучаемого признака, т. е. рассчитывается на достаточном числе наблюдений. Средние величины получают из рядов распределения (вариационных рядов). Вариационный ряд — ряд однородных статистических величин, характеризующих один и тот же количественный учетный признак, отличающихся друг от друга по своей величине и расположенных в определенном порядке (возрастания или убывания). Элементами вариационного ряда являются: • Варианта — V(X) — числовое значение изучаемого меняющегося ко ■ Частота — р (pars), или f (frequency) — повторяемость вариант в вариационном ряду, показывающая, как часто встречается та или иная варианта в составе данного ряда. • Общее число наблюдений — п (numerus) — сумма всех частот (где п Виды вариационных рядов: 1. В зависимости от значения варианты (V): прерывные (дискретные) Вариационные ряды могут быть прерывные (дискретные), состоящие из целых чисел, и непрерывные, когда значения вариант выражены дробным числом. В прерывных рядах смежные варианты отличаются друг от друга на целое число, например: число ударов пульса, число дыханий в минуту, число детей в семье, число дней лечения и т. д. В непрерывных рядах варианты могут отличаться на любые дробные значения единицы, например, при изучении веса взрослых можно ограничиться килограммами, а при изучении веса новорожденных — граммами. 2. В зависимости от частоты встречаемости признака (р): простой, Простой ряд — каждая варианта встречается один раз, т. е. частоты равны единице (р=1). Обычный ряд — варианты встречаются более одного раза (р>1). Сгруппированный ряд — варианты объединены в группы по их величине в пределах определенного интервала с указанием частоты повторяемости всех вариант, входящих в группу. Сгруппированный вариационный ряд используют при большом числе наблюдений и большом размахе крайних значений вариант. 3. В зависимости от числа наблюдений (п): а) четные и нечетные; б) большой (при числе наблюдений больше 30, п >30), малый (если число При изучении достаточно большого числа наблюдений в распределении вариант в вариационных рядах имеются определенные закономерности. 1. Большинство вариант часто располагаются в средней части вариационного ряда. 2. Распределение вариант в обе стороны от этого максимума более или менее симметрично. 3. Частоты вариант постепенно убывают к краям вариационного ряда. Виды средних величин В медицинской практике наиболее часто используются следующие средние величины: мода, медиана, средняя арифметическая. Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определении среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей), средняя прогрессивная и др. Мода (Мо) — величина признака, чаще других встречающаяся в совокупности. За моду принимают варианту, которой соответствует наибольшее количество частот вариационного ряда. Медиана (Me) — величина признака, занимающая срединное положение в вариационном ряду. Она делит вариационный ряд на две равные части. Для определения медианы следует найти ее порядковый номер в вариационном ряду по формуле, а затем установить ее числовое значение:
Зная порядковый номер медианы в вариационном ряду, определяют ее числовое значение. На величину моды и медианы не оказывают влияния числовые значения крайних вариант, имеющихся в вариационном ряду. Мода и медиана применяются в медицинской статистике относительно редко. Более точно характеризует вариационный ряд средняя арифметическая величина, которая чаще других средних величин используется в медицинской статистике. Средняя арифметическая (М, или X) — рассчитывается на основе всех числовых значений изучаемого признака. В простом вариационном ряду, где варианты встречаются только по одному разу, вычисляется средняя где V — числовые значения вариант, п — число наблюдений, Σ — знак суммы. В обычном вариационном ряду вычисляется средняя арифметическая взвешенная по формуле: где V — числовые значения вариант, р — частота встречаемости вариант, п — число наблюдений, Σ — знак суммы. Таблица 6 Определение средней длительности лечения больных в специализированном отделении больницы за 2... г.
В приведенном примере 6 (табл.6) модой является варианта, равная 20 дням, поскольку она повторяется чаще других — 29 раз. Мо = 20 дней. Порядковый номер медианы приходится на 48-ю варианту
Средняя арифметическая, рассчитанная по формуле, равна 20 дням. Средняя величина — именованная величина, она выражается в тех же единицах измерения, что и варианта (днях, килограммах, метрах и т. д.) Средние величины являются важными обобщающими характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака. Если вариационный ряд более компактен, менее рассеян и все отдельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариационный ряд растянут, отдельные значения значительно отклоняются от средней, т. е. имеется большая вариабельность количественного признака, то средняя менее типична, недостаточно точно отражает в целом весь ряд. Одинаковые по величине средние могут быть получены из рядов с различной степенью рассеяния. Так, например, средняя длительность лечения больных в специализированном отделении больницы также будет равна 20 дням, если все больные находились на стационарном лечении по 20 дней. Обе вычисленные средние равны между собой, но получены из рядов с разной степенью разнообразия вариант. Следовательно, для характеристики вариационного ряда, помимо средней величины, необходима другая характеристика, позволяющая оценить степень его разнородности. Простыми показателями, характеризующими разнообразие признака в изучаемой совокупности, являются лимит и амплитуда. Лимит — это минимальное и максимальное значения количественного тризнака. В примере 6 лимит = 16 и 24 дня. Амплитуда — это разность между наибольшим и наименьшим значени-гм вариант (Vmax -- Vmin). В примере 6 амплитуда = 24 - 16 = 8 дней. Чем меньше амплитуда колебания ряда (степень рассеяния ряда), тем бо-iee точно его будет характеризовать средняя арифметическая. Однако лимит и амплитуда не учитывают значений вариант внутри ряда. Дата добавления: 2015-02-06 | Просмотры: 1777 | Нарушение авторских прав |
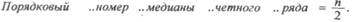
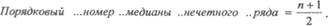
 арифметическая простая по формуле:
арифметическая простая по формуле: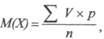

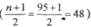 , числовое значение которой равно 20. Me = 20 дней.
, числовое значение которой равно 20. Me = 20 дней.