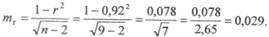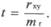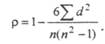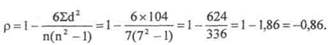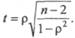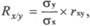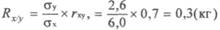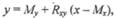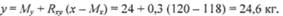|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Обратно косвенный метод стандартизации (Керриджа)Применяется при отсутствии данных о составе среды и ее распределении по группам, когда имеются лишь сведения о возрастном, половом составе больных, родившихся или умерших и т. д., т. е. данные обратные тем, что использовались при косвенном методе стандартизации. Метод дает менее точные результаты. КОРРЕЛЯЦИЯ (взаимосвязь) Многие явления в медицине, так же. как в природе и обществе, взаимосвязаны между собой. При проведении статистического исследования часто возникает необходимость проанализировать выявленные связи между различными явлениями и дать обобщающую характеристику. Различают 2 формы проявления связей между явлениями: функциональную и корреляционную. Функциональная связь означает строгую зависимость одного признака от другого, когда определенному значению одной величины соответствует строго определенное значение другой. Например, радиусу крута соответствует определенная площадь круга; скорость свободно падающего тела определяется величиной ускорения, силой тяжести и временем падения. Функциональная связь характерна для физико-химических процессов. Корреляционная связь — это такая связь, когда одной и той же величине одного признака соответствует несколько значений другого взаимосвязанного с ним признака. Врачи и биологи хорошо знакомы с этим видом связи: при одинаковой температуре у различных людей наблюдаются индивидуальные колебания частоты пульса; при одинаковом росте отмечаются различные колебания масс тела. Корреляционная связь проявляется между ростом детей и их родителей, массой тела и ростом, числом эритроцитов и содержанием гемоглобина, дозой зараженного агента и летальностью животных и т. д. Корреляционная связь проявляется лишь для всей совокупности наблюдений, тогда как функциональная связь имеет место в каждом отдельном наблюдении. Корреляционная зависимость отличается по форме, направлению и силе связи. По форме корреляционная связь может быть прямолинейной и криволинейной. Прямолинейная связь — равномерные изменения одного признака соответствуют равномерным изменениям второго признака при незначительных отклонениях. Криволинейная связь — равномерные изменения одного признака, соответствуют неравномерным изменениям второго признака, причем неравномерность имеет определенную закономерность. Общая тенденция в определенном моменте изменяет свое направление, дает изгиб. Направление связи может быть прямое (положительное) или обратное (отрицательное). Прямая связь — если с увеличением одного признака второй также увеличивается или с уменьшением одного признака другой тоже уменьшается. Например, с увеличением роста увеличивается масса тела, с уменьшением заболеваемости уменьшается смертность. Обратная связь — когда с увеличением одного признака, другой, корреляционно связанный с ним признак, уменьшается. Например, с увеличением охвата населения прививками уменьшается заболеваемость инфекционными болезнями, с увеличением санитарной грамотности и образованием матери уменьшается младенческая смертность. Под силой связи следует понимать степень корреляции (степень сопряженности между признаками). Измерение силы связи и определение ее направления осуществляется путем вычисления коэффициента корреляции. Существуют следующие методы вычисления коэффициента корреляции: рядов, рангов, путем составления корреляционной решетки. Таблица 13 Критерии оценки коэффициента корреляции
Рассмотрим способы расчета коэффициента корреляции рядов {rху) и коэффициента корреляции рангов (р). I. Коэффициент корреляции рядов (гxy) вычисляется по формуле:
Алгоритм расчета коэффициента корреляции рядов (г^,) приведен в примере 18 (табл. 14). При сопоставлении показателей содержания железа и гемоглобина в крови отмечается увеличение уровня гемоглобина с ростом количества железа. Следует определить степень и направление связи между этими показателями и достоверность полученного результата. Таблица 14 Зависимость уровня гемоглобина от количества содержания железа в крови
Вычисления проводятся по следующему алгоритму:
2. Определяем отклонения вариант каждого ряда от своей средней (dx и dx=Vх-Mх; dy = Vy - My 3. Находим произведение dx на dy (графа 5, табл. 14). Полученные значения суммируются с учетом знаков. 4. Возводим в квадрат dx и dy суммируем полученные значения (графа 6 и 7, табл. 14): 5. Вычисляем коэффициент корреляции:
Вывод: Так как коэффициент корреляции гxy = +0,92, следовательно, между содержанием в крови железа и гемоглобина отмечается сильная и прямая корреляционная связь, т. е. чем больше содержание железа в крови, тем выше уровень гемоглобина. Поскольку исследование проводилось на выборочной совокупности, необходимо оценить достоверность коэффициента корреляции. Для оценки достоверности коэффициента корреляции вычисляется его средняя ошибка:
В рассмотренном примере 18 следует использовать последнюю формулу, поскольку число наблюдений равно 9:
Для оценки величины полученной ошибки следует использовать критерий достоверности (t).
Значение критерия (t) оценивается по специальной таблице Стьюдента. Если полученное значение (t) больше табличного для выбранного уровня доверия и числа степеней свободы, то коэффициент корреляции считается достоверным. В рассмотренном примере t = 37,1. Это значение больше табличного, что подтверждает достоверность выяв-пенной сильной связи и взаимозависимости анализируемых явлений. II. Коэффициент корреляции рангов (р) относится к непараметриче-:ким критериям и предложен Спирменом. Он используется при необходимости получения быстрого результата, при малом числе наблюдений, а также в тех случаях, когда изучаемые признаки не имеют точных количественных значений дли носят описательный характер. Этот метод основан на определении ранга места) каждого из значений ряда. Для вычисления коэффициента корреляции рангов используется следующая формула: где р — (греческая буква «ро») — коэффициент корреляции рангов; d — разность между ранговыми номерами; п — число парных членов в коррелируемых рядах. Пример 19: вычислить коэффициент корреляции рангов между величиной расходов на здравоохранение на душу населения и смертностью детей в возрасте до 5 лет (таблица 15). Таблица 15 Зависимость смертности детей в возрасте 5 лет от расходов на здравоохранение на душу населения в странах в 1997 г.
При сопоставлении показателя смертности детей в возрасте до 5 лет и расходов на здравоохранение на 1 жителя (SCIIIA) отмечается снижение частоты смерти детей в возрасте до 5 лет с увеличением расходов на здравоохранение. Следует определить степень связи между этими показателями и достоверность полученного результата. Вычисления проводятся по следующему алгоритму: 1. Определить ранги по значению каждой величины ряда. Если первый ряд (х) ранжируется от меньшего значения к большему, то второй ряд (у) следует ранжировать в том же порядке (графа 4 и 5, табл. 15). 2. Определить разность рангов каждой пары ряда (х) и ряда (у): (dxy)= (х) - (у) (графа 6, табл. 15). Они в сумме с учетом знаков равны нулю. 3. Возвести в квадрат полученные разности и суммировать их. В нашем примере Σd2xy = 8 (графа 7, табл. 15). 4. Рассчитываем коэффициент корреляции рангов:
Вывод: связь сильная, обратная (р = -0,86). Между смертностью детей в возрасте до 5 лет и расходами на здравоохранение на 1 жителя существует сильная и обратная связь, с увеличением расходов на здравоохранение снижается смертность детей в возрасте до 5 лет. Прежде чем судить о степени связи между изучаемыми признаками, необходимо оценить достоверность коэффициента корреляции рангов. При п > 9 следует рассчитать критерий t по формуле:
Полученное значение критерия t оценивается по таблице Меритерия Стьюдента для числа степеней свободы n' = л-2. Если п < 9, оценка достоверности коэффициента корреляции рангов проводится по специальной таблице критических значений коэффициента корреляции Спирмена (р). Коэффициент корреляции незначим, если рассчитанное значение меньше табличного. РЕГРЕССИЯ Прямолинейная корреляция отличается тем, что при этой форме связи каждому значению одного признака соответствует определенное в среднем значение другого признака. Рассмотренный нами коэффициент корреляции указывает лишь на направление и силу связи двух величин, не дает судить о том, как количественно меняется величина признака по мере изменения другой величины. Применение метода регрессии позволяет ответить на этот вопрос. Та величина, на которую в среднем изменяется второй признак при изменении первого на единицу, называется коэффициентом регрессии. Для расчета коэффициента регрессии (Rx) используется следующая формула:
где σх и σу — среднеквадратические отклонения ряда X и ряда Y; г^ — коэффициент корреляции. Рассмотрим методику расчета коэффициента регрессии на примере 20. При анализе физического развития 7-летних мальчиков были получены следующие средние значения роста M(x) и массы тела М(у): М(х) = 118,4 см σх = ± 6,0 см; М(у) = 24,0 кг σу = ± 2,6 кг. Коэффициент корреляции (гху) между весом и ростом составил +0,7. Расчет коэффициента регрессии выполняется по формуле:
Вывод: с изменением роста 7-летних мальчиков на 1 см, масса тела в среднем изменяется на 0,3 кг. С помощью коэффициента регрессии без специальных измерений можно определить величину одного из признаков, например, массы тела, зная значение другого (роста). С этой целью используется уравнение линейной регрессии: где у — искомая величина массы тела; Му — среднее значение массы тела, характерное для данного возраста; Rxy —- коэффициент регрессии массы тела по росту; х — известная величина роста; Мх — среднее значение роста. Пример 21: определим, какова будет масса тела 7-летних мальчиков при росте 120 см, если среднее значение массы Myравно 24 кг, а средний рост равен 118 см. Подставим в уравнение линейной регрессии известные данные и получим:
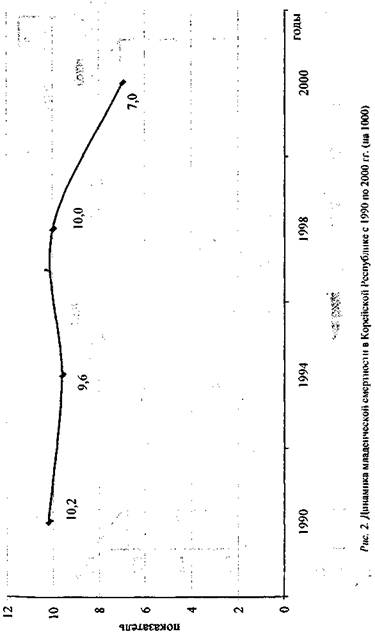
Вывод: группа 7-летних мальчиков с ростом 120 см должна иметь среднюю массу тела 24,6 кг. Коэффициенты регрессии и уравнения линейной регрессии широко применяются для составления шкал регрессии, которые используются при индивидуальной оценке физического развития. ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ Результаты статистического исследования могут быть представлены в виде графических изображений, что позволяет более наглядно продемонстрировать полученные данные и облегчает проведение анализа. Диаграммы можно классифицировать различными способами. По назначению — диаграммы сравнения, структурные, динамики явления; по форме — линейные, плоскостные и объемные. Графические изображения отражают закономерность развития, пространственные распределения, взаимосвязь явлений. Графические изображения помогают эффективному анализу статистических данных. Наиболее часто используют диаграммы (линейные, радиальные, столбиковые, ленточные, секторные, внутристолбиковые и др.), картограммы, картодиаграммы (рис. 2-8). Линейные диаграммы позволяют отображать динамику явления (изменение показателей во времени). Линейная диаграмма строится в системе прямоугольных координат, при ее построении следует учитывать соотношение между основанием (ось абсцисс —x ) и высотой (ось ординат— у), оно должно быть 1,6:1. На ось абсцисс откладываются отрезки, обозначающие периоды времени. На ось ординат наносятся размеры изучаемого явления. Обязательное условие при построении графика — соблюдение масштаба. На одной диаграмме можно изобразить несколько линий, отличающихся Друг от друга цветом, толщиной или формой пунктира. Радиальные диаграммы (полярных координат, линейно-круговые, векторные) применяются для изображения сезонных (подекадных, помесячных, поквартальных) и других колебаний, имеющих замкнутый, циклический характер (за сутки, неделю и т. д.)- Для их построения круг делится на столько секторов, на сколько частей разделен период времени, взятый для изучения явления (например, на 12 — при изучении помесячных колебаний в течение года; на 7 — при изучении явления за неделю). На каждом из радиусов с соблюдением масштаба отмечаются показатели, полученные точки соединяются прямыми линиями. Маркировка начинается с радиуса, соответствующего нулю градусов, и продолжается по движению часовой стрелки. Столбиковые диаграммы строятся по такому же принципу, как и линейные, в системе координат. В них размеры изучаемого явления изображены в виде прямоугольников. Эти диаграммы используются для сравнения величины изучаемого явления за определенные промежутки времени или на какой-то момент времени, например: сравнительной численности населения по странам мира; обеспеченности населения врачами в разные годы и т. д. Гистограммы — это изображения в виде прямоугольников, треугольников и других фигур однородных статистических показателей, не связанных друг с другом. Эти диаграммы используются для графического изображения статистических величин, рассчитанных в разных совокупностях. Они также строятся в системе прямоугольных координат с соблюдением масштаба. Например, гистограммы применяются для графического изображения уровней смертности в разных возрастных группах населения; для демонстрации показателей больничной летальности в различных стационарах города; для изображения распространенности туберкулеза в различных социальных группах населения и т. д. Секторные диаграммы используются для демонстрации структуры изучаемого явления, изображения части в целом явлении. Они представляют собой круг, принимаемый за целое (100%, при этом 1% соответствует 3,6 градуса окружности), в котором отдельные секторы соответствуют частям отображаемого явления. Этот вид диаграмм применяется для графического изображения экстенсивных показателей. Секторы, изображающие отдельные части изучаемого явления, располагаются в порядке возрастания или убывания по движению часовой стрелки и имеют разный цвет или штриховку. Внутристолбиковые диаграммы также могут применяться для изображения структуры явления. При этом высота столбика принимается за 100%, весь столбик делится на составные части, которые соответствуют долям явления в процентах. Картограммы — это графические изображения, нанесенные на географической карте, где различным цветом или штриховкой изображена степень распространенности явления по территории. Они иллюстрируют интенсивность статистических показателей в географических, административных районах, по- зволяют установить соответствие между статистической величиной и ее пространственным распределением. Картодиаграммы — графические изображения, при построении которых на карту или схему карты изучаемой территории наносятся диаграммы (столбиковые, фигурные, линейные). При построении графических изображений необходимо соблюдать следующие правила: - данные на графике размешаются слева направо и снизу вверх; - обязательное условие при построении графика — соблюдение масштаба; - нулевые точки шкал изображаются на диаграмме; - цифры, показывающие деление шкал, располагаются слева или внизу соответствующей шкалы; - линии, изображающие явление, представляются в ином виде, чем вспомогательные (цвет, толщина); - на кривой, отражающей динамику явления, отмечаются все точки, соответствующие отдельным наблюдениям; - в диаграммах, показывающих структуру, должна быть оттенена как нулевая, так «100%-ная линия: - изображенные графические величины должны иметь цифровые обозначения на самом графике или в прилагаемой к нему таблице; - символы, используемые при построении диаграммы (цвет, штриховка, фигуры, знаки), должны быть пояснены; - каждый график должен иметь четкое, краткое название, отражающее его содержание, порядковый номер; - название диаграммы располагается под рисунком.
Приложение Таблица значений критерия / (Стьюдента)
Дата добавления: 2015-02-06 | Просмотры: 1796 | Нарушение авторских прав |
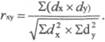
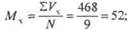
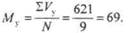
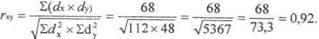
 — при числе наблюдений более 100;
— при числе наблюдений более 100; — при числе наблюдений от 30 до 100;
— при числе наблюдений от 30 до 100; — при числе наблюдений менее 30.
— при числе наблюдений менее 30.