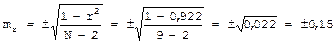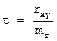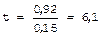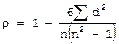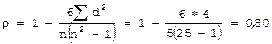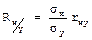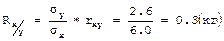|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Оценка достоверности разницы статистических величинПри проведении медико-биологических исследований на двух сравниваемых совокупностях возникает необходимость определить не только их различие, но и его достоверность. Для оценки достоверности различия сравниваемых средних величин используется формула:
где Μ1, Μ2, P1 и P2 - статистические величины, полученные при проведении выборочных исследований: m1 и m2 - их ошибки репрезентативности; t - коэффициент достоверности. Различие достоверно при t>2. что соответствует вероятности безошибочного прогноза равной или более 95%. При величине коэффициента достоверности t<2 степень вероятности безошибочного прогноза менее 95%. При такой степени вероятности мы не можем утверждать, что полученная разность показателей достоверна с достаточной степенью вероятности. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений. Если после увеличения численности выборки, и. соответственно, уменьшения ошибки репрезентативности, различие продолжает оставаться недостоверным, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку. В качестве примера сопоставим уровни общей летальности в двух больницах:
а) рассчитываем средние ошибки показателей летальности (Р1 и Р2).
б) вычисляем критерий достоверности t:
Рассчитанный критерий достоверности равен 10, он больше 2, что указывает на существенную разницу уровней летальности в сравниваемых больницах. Корреляционный анализ Многие явления в медицине, так же, как в природе и обществе, взаимосвязаны между собой. При проведении статистического исследования часто возникает необходимость проанализировать выявленные связи между различными явлениями и дать обобщающую характеристику. Различают 2 Формы проявления связей между явлениями: функциональную и корреляционную. Функциональная связь означает строгую зависимость одного признака от другого, когда определенному значению одной величины соответствует стр о г о определенное значение другой. Например, радиусу круга соответствует определенная площадь круга; скорость свободно падающего тела определяется величиной ускорения, силы тяжести и времени падения. Функциональная связь характерна для физико-химических процессов. Корреляционная связь - это такая связь, когда изменение какого-либо одного признака ведет к изменению другого, но на неопределенное значение. Врачи и биологи хорошо знакомы с этим видом связи. Корреляционная связь проявляется между ростом детей и их родителей, массой тела и ростом, числом эритроцитов и содержанием гемоглобина, дозой зараженного агента и летальностью животных и т.д. Корреляционная зависимость отличается по форме, направлению и силе связи. По форме корреляционная связь может быть прямолинейной и криволинейной. Прямолинейная связь - равномерные изменения одного признака соответствуют равномерным изменениям второго признака при незначительных отклонениях. Криволинейная связь - равномерные изменения одного признака, соответствуют неравномерным изменениям второго признака, причем неравномерность имеет определенную закономерность. Общая тенденция в определенном моменте изменяет свое направление, дает изгиб. Направление связи может быть прямое (положительное) или обратное (отрицательное). Прям а я связь - если с увеличением одного признака второй также увеличивается или с уменьшением одного признака другой тоже уменьшается. Например, с увеличением роста увеличивается масса тела, с уменьшением заболеваемости уменьшается смертность. Обратн а я связь - когда с увеличение одного признака, другой, корреляционно связанный с ним признак, уменьшается. Например, с увеличением охвата прививками уменьшается заболеваемость инфекционными болезнями, с увеличением санитарной грамотности и образованием матери уменьшается младенческая смертность. Под силой связи следует понимать степень корреляции. Таблица 7 Критерии оценки коэффициента корреляции
Измерение силы связи осуществляется путем вычисления коэффициента корреляции. Рассмотрим два способа расчета коэффициента корреляции. I. Парный коэффициент корреляции рядов (rху) вычисляется по формуле:
Рассмотрим на примере методику расчета коэффициента корреляции этим методом (Таблица 8). Таблица 8
При сопоставлении показателей содержания железа и гемоглобина в крови отмечается увеличение уровня гемоглобина с ростом количества железа. Следует определить степень связи между этими показателями и достоверность полученного результата. Вычисления проводятся по следующему алгоритму: 1) Вычисляем средние арифметические рядов X и Y:
2) Определяем отклонения вариант каждого ряда от своей средней (dx и dу): смотри графы 3 и 4 в Таблице 3. 3) Находим произведение dx*dy: смотри графу 5 в Таблице 8. Полученные значения суммируются с учетом знаков. 4) Возводим в квадрат dx и dy и суммируем полученные значения: смотри графы 6 и 7 в Таблице 8. 5) Вычисляем коэффициент корреляции:
Вывод: Отмечается очень сильная корреляционная связь между содержанием в крови железа и гемоглобина.
Для оценки достоверности коэффициента корреляции вычисляется его средняя ошибка:
В рассматриваемом нами примере следует использовать последнюю формулу, поскольку число наблюдений равно 9:
Для оценки величины полученной ошибки следует использовать критерий достоверности (t).
При числе наблюдений более 30 коэффициент корреляции достоверен, если критерий t больше или равен 3. При числе наблюдений менее 30 критерий t оценивается по специальной. В рассматриваемом нами примере Это больше табличного значения, что подтверждает достоверность выявленной сильной связи и взаимозависимости анализируемых явлений. II. Ранговый коэффициент корреляции (ρ) относится к непараметрическим критериям и предложен Спирменом. Он используется при необходимости получения быстрого результата и основан на определении ранга (места) каждого из значений ряда. Для вычисления рангового коэффициента корреляции используется следующая формула:
Рассмотрим методику вычисления рангового коэффициента корреляции на следующем примере (Таблица 9). Таблица 9.
При сопоставлении частоты травматизма и распространенности гнойничковых заболеваний среди рабочих промышленного предприятия отмечается рост гнойничковых заболеваний с увеличением травматизма. Следует определить степень связи между этими показателями и достоверность полученного результата. Вычисления проводятся по следующему алгоритму: 1) Определяем ранги по значению каждой величины ряда. Важно соответствие. Если первый ряд ранжируется от меньшего значения к большему, то второй ряд следует ранжировать в том же порядке. 2) Отмечаем отклонение значимости рангов первого ряда от второго (dxy): смотри графу 6 в таблице 9. Они в сумме с учетом знаков равны нулю. 3) Возводим в квадрат полученные отклонения и суммируем их. В нашем примере d2xy = 4: смотри графу 7 в таблице 9. 4) Рассчитываем ранговый коэффициент корреляции:
Вывод: Корреляция прямая, высокая. Между травматизмом и частотой гнойничковых заболеваний на предприятии существует тесная связь. Оценка достоверности полученного рангового коэффициента корреляции выполняется по методике, которая была разобрана для коэффициента корреляции рядов. Регрессионный анализ Прямолинейная корреляция отличается тем, что при этой Форме связи каждому значению одного признака соответствует определенное в среднем значение другого признака. Та величина, на которую в среднем изменяется второй признак при изменении первого на единицу, называется коэффициентом регрессии. Для расчета коэффициента регрессии используется следующая формула:
Рассмотрим методику расчета коэффициента регрессии на примере. При анализе физического развития 7-летних мальчиков были получены следующие средние значения роста (X) и массы тела (У):
Коэффициент корреляции между весом и ростом составил +0.7. Расчет коэффициента регрессии выполняется по формуле:
Следовательно, с изменением роста 7-летних мальчиков на 1 см. масса тела в среднем изменяется на 0.3 кг. С помощью коэффициента регрессии без специальных измерений можно определить величину одного из признаков (например, массы тела), зная значение другого (роста). С этой целью используется ур а внени е лине й ной регрессии: у = My + Rxy(х - Мх), где у - искомая величина массы тела; My - среднее значение массы тела, характерное для данного возраста; Rxy - коэффициент регрессии массы тела по росту; х - известная величина роста; Мх - средне значение роста. Определим, какова будет масса тела 7-летнего мальчика при росте 120 см. у = Мy + Rxy(х - Мх) = 24 + 0.3(120 - 118) = 24.6 кг Коэффициенты регрессии и уравнения регрессии широко применяются для составления шкал регрессии, которые используются при индивидуальной оценке физического развития. Дата добавления: 2015-02-06 | Просмотры: 1054 | Нарушение авторских прав |
 ,а для относительных величин:
,а для относительных величин:  ,
,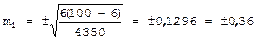
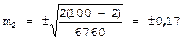

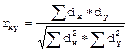
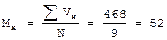


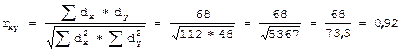
 - при числе наблюдений более 100;
- при числе наблюдений более 100; - при числе наблюдений от 30 до 100;
- при числе наблюдений от 30 до 100; - при числе наблюдений менее 30.
- при числе наблюдений менее 30.