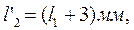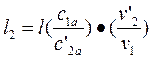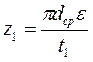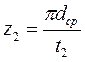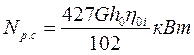|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Расчет регулирующей ступени1. Расчет проточной части регулирующей ступени производят на секундный расход пара с учетом утечки через переднее концевое уплотнение:
где Dут — часовой расход пара через переднее концевое уплотнение причем Dут = 3600Gyт. Формула для определения Gyт приведена в разд. 3—2. 2. Изоэнтропийным теплоперепадом h0, перерабатываемым на регулирующей ступени, задаются, руководствуясь следующими соображениями. Высокое значение, теплоперепада приводит к упрощению конструкции турбины, т. е. к уменьшению числа ступеней и удешевлению турбины; но при этом снижается к. п. д. Выбор малого теплоперепада приводит к увеличению числа ступеней, т. е. удорожает турбину, но к. п. д. повышается. В отечественных турбинах малой и средней мощности h0 выбирают в пределах 210—290 кДж/кг (50—70 ккал/кг) Для вновь проектируемых мощных турбин принимают h0 = 85÷ 105 кДж/кг (20÷25 ккал/кг) Выбор относительно большого теплоперепада h0 = 210 ÷ 290 кДж/кг в турбинах малой и средней мощности вызван тем, что: а) большое влияние на к. п. д. турбины оказывает утечка пара через переднее концевое уплотнение, а чем ниже давление пара в камере регулирующей ступени, тем меньше утечка; б) при пониженном давлении в камере регулирующей ступени с большей степенью парциальности можно выполнить последующие ступени при достаточно высоких соплах и лопатках, что приведет к снижению потерь на вентиляцию. Выбор относительно малого теплоперепада (h0=85 ÷105 кДж/кг) в турбинах большой мощности объясняется тем, что при больших объемных расходах пара через турбину утечка через переднее концевое уплотнение незначительна и мало влияет на к. п. д. турбины, а последующие ступени давления всегда можно осуществить с полным впуском пара при достаточно высоких соплах и рабочих лопатках 3. В качестве регулирующей ступени для многоступенчатых турбин применяют как одновенечный диск Рато, так и двухвенечный диск Кертиса. Первый используется при переработке небольших теплоперепадов на регулирующей ступени и обладает относительно высоким к. п. д. при работе турбины в расчетном режиме. Второй применяется при переработке больших теплоперепадов и характеризуется более постоянным к. п. д. при различных режимах работы турбины. Последнее обстоятельство объясняется тем, что при эксплуатации турбины отклонение от расчетного режима в диске Кертиса меньше сказывается на изменении отношения u/c1, чем в диске Рато. 4. Для уменьшения подсоса пара и увеличения к. п. д. регулирующей ступени на рабочих и направляющих лопатках диска Кертиса вводят реактивность, что целесообразно при полном впуске пара. При парциальном впуске пара и малой высоте лопаток введение реактивности не всегда полезно, так как при этом могут возрасти потери энергии от утечки пара через зазор между лопатками и корпусом турбины, что вызовет понижение к. п. д. турбины. При малом расходе, высоких и средних начальных параметрах принимают, что степень реакции ρ к = 0. 5. Теоретическую скорость истечения пара из сопла для диска Кертиса рассчитывают по формулам: в единицах СИ
в единицах системы МКГСС
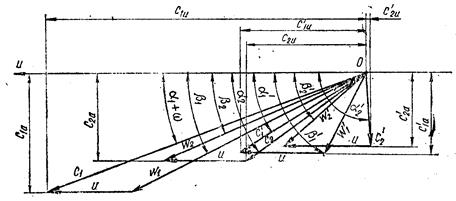
Здесь h0 – изоэнтропийный перепад, приходящий на диск Кертиса; ρк=ρн+ρр – суммарная степень реакции, где ρн — степеньреакции, приходящейся на направляющие лопатки турбины, ρр — степень реакции, приходящейся на рабочие лопатки. Обычно ρн = 0,02, ρρ = 0,02 ÷0,04, так что ρ к, = 0,04÷0,06. 6. Действительная скорость истечения пара из сопла с1 =φс1t где φ — скоростной коэффициент сопла. Последний определяют по формуле
в которой xc-коэффициент потери энергии в сопловой решетке. При известных режимных и геометрических параметрах сопла (выбор профиля сопла описывается в п. 15) коэффициент xc-находят из книги Дейча М. Е. и др. «Атлас профилей решеток осевых турбин» (М., «Машиностроение», 1965). Если же атласа нет или необходимые для расчета данные в нем отсутствуют, то скоростной коэффициент φ выбирают в зависимости от степени обработки поверхностей сопла: при грубо отлитых соплах φ = 0,93 ÷ 0,94; при тщательно отлитых и обработанных соплах φ = 0,95 ÷0,96; при тщательно фрезерованных соплах φ = 0,96 ÷0,97. Часто принимают φ = 0,95. 7. Чтобы найти оптимальное значение отношения окружной скорости и к действительной скорости истечения пара из сопла си задаются рядом отношений u/c1 для двухвенечного диска Кертиса эти отношения берут в пределах 0,20÷0,26 для чисто активных ступеней и 0,23÷0,32 для ступеней с небольшой степенью реакции; для одновенечных дисков с небольшой степенью реакции — в пределах 0,42÷0,58.
Рис. 8. Построение треугольников скоростей для диска Кертиса 8. Задаются углами наклона сопел ai: для одновенечных ступеней в пределах 11—16°; для двухвенечных»»» 16—22°; для трехвенечных»»» 20—24°. 9. По выбранным отношениям u/c1 строят треугольники скоростей для диска Кертиса (рис. 8). Из точки 0 под углом аi +ω (ω — угол отклонения струи пара косым срезом) к оси 0и откладывают вектор с1. И з конца вектора с1 в сторону, противоположную направлению оси 0u, откладывают вектор окружной скорости u=u\c1 c1=u Соединив начало вектора и с точкой 0, получают вектор относительной скорости пара на входе первого ряда рабочих лопаток ω1и входной угол β1 Чтобы построить выходной треугольник скоростей для первого ряда рабочих лопаток (он же — входной треугольник для направляющих лопаток), определяют выходной угол β2 и относительную скорость на выходе первого ряда рабочих лопаток w2:
где ψ- скоростной коэффициент на рабочих лопатках. Коэффициент ψ рассчитывают по формуле, в которой xл — коэффициент потерь энергии в рабочей решетке.
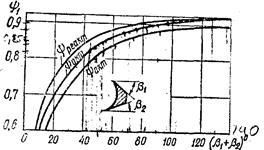
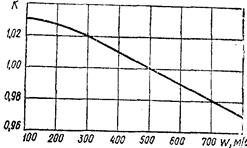
При известных режимных и геометрических параметрах лопаток (выбор лопаток описывается в п. 15) коэффициент xл находят из упомянутого атласа Дейча М. Е.. Если же атласа нет или необходимые для расчета данные в нем отсутствуют, то скоростной коэффициент ψ определяют из графика (рис. 9), который используют при относительной скорости пара около 500 м/с как для активных (ψ акт), так и для реактивных (ψ реакт) ступеней. При других скоростях найденное значение ψ нужно умножить на коэффициент к, определяемый из рис. 10.
Рис. 9. График для определения скоростного коэффициента ψ в зависимости от угла поворота струи
Рис. 10. График для определения поправочного коэффициента, учитывающего скорость пара Отложив вектор w2 из точки 0 под углом β2 к оси 0u, из конца этого вектора в направлении, противоположном направлению оси 0u откладывают вектор и. Соединив точку 0 с началом вектора и, получают вектор с2 — абсолютную скорость пара на выходе из первого ряда рабочих лопаток, направленную под углом а2к оси Ои. Скорость с2 является одновременно абсолютной скоростью пара на входе направляющих лопаток. Абсолютную скорость пара на выходе из направляющих лопаток с учетом степени реакции ρн рассчитывают по формулам: в единицах СИ
в единицах системы МКГСС
Вектор скорости с’1 направлен под углом а’1 к оси Ои, причем
Величину скоростного коэффициента пара на направляющих лопатках ψннаходят с помощью графиков, изображенных на рис. 9 и 10, полагая ψн=f (а2 + а’1).Относительную скорость пара на входе второго ряда рабочих лопаток w’1 определяют путем построения треугольника скоростей. Для этого из точки 0 проводят вектор скорости c’1 под углом a’1 к оси Ои. Из конца этого вектора в направлении, противоположном направлению оси Ои, откладывают вектор и. Соединив точку 0 с началом вектора и, получают вектор w’1, направленный под углом β’1 к оси Ou. Чтобы построить выходной треугольник скоростей, определяют относительную скорость на выходе второго ряда рабочих лопаток w’2: единицах СИ
в единицах системы МКГСС
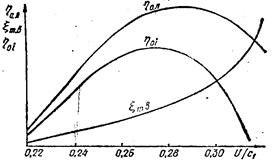
Рис. 11. Зависимость коэффициентов ηо.п, ηоi и поправки ξт в от отношения i/c1
Здесь ρр — степень реакции на втором ряду рабочих лопаток; h0 — теплоперепад, приходящийся на регулирующую ступень турбины; ψр — скоростной коэффициент на рабочих лопатках, определяемый из графиков (рис. 9 и 10), причем ψр =f(β’1 + β’2), а угол β’2 = [β’1 - (3÷5)]°. Из точки 0 под углом β2 откладывают вектор w’2. Из конца этого вектора в направлении, противоположном оси Оu, откладывают вектор и. Соединив начало вектора и с точкой 0, получают вектор с’2 — абсолютную скорость пара на выходе из второго ряда рабочих лопаток, направленную под углом а’2 к оси Оu. Затем проектируют абсолютные скорости на ось Оu. Аналогично строят треугольники скоростей для остальных выбранных отношений u/c1. При этом угол а1 для всех отношений u/c1 остается неизменным. 10.Результаты построения треугольников скоростей, значения относительного к. п. д. на лопатках ηо.л, высоту сопел l; степень парциальности ε; среднюю арифметическую высоту рабочих лопаток l1ср, потери на трение и вентиляцию N’T.B; поправку xт.в, а также внутренний относительный к. п. д. ступени ηо.i для всех выбранных отношений u/c1 записывают в табл. 1. 11. На основании табл. 1 строят кривую зависимости ηо.л =f(u/c1) (рис. 11). Для определения оптимального отношения u/c1 нужно установить зависимость ηо.i=f(u/c1).Для этого необходимо учесть потери на трение и вентиляцию, поскольку потери через внутренние уплотнения не зависят от u/c1. 12. Потери на трение и вентиляцию определяют по формуле Стодола, которую Бауэр для дисков Кертиса представил в следующем виде:
Здесь λ — коэффициент, принимающий значения: 1 — для высоко перегретого пара, 1,1—1,2 — для перегретого пара, 1,3 — для насыщенного пара; d — диаметр ступени, z — число венцов;
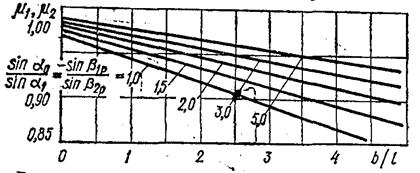
Рис. 12, График для определения коэффициента расхода для сопловых и рабочих решеток
μ1- коэффициент расхода, определяемый из графика (рис. 12); Go — секундный расход пара, кг/с; v1 — удельный объем пара в выходном сечении сопла, м3/кг; l— высота сопел (выбираемая величина, которая должна быть больше 10 мм). Потери на трение и вентиляцию для 1 кг пара, прошедшего через регулирующую ступень, определяют по формулам: в единицах СИ
в единицах системы МКГСС
Таблица 1.
Коэффициент, учитывающий эти потери, рассчитывают по формуле
авнутренний относительный к. п. д. регулирующей ступени — и по формуле
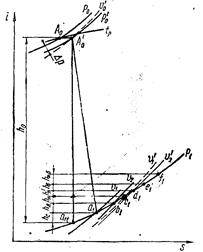
Определив значения ξT.B для выбранных отношений u/c1, занося их в табл. 1 и строят кривую зависимость ξт.в = f(u/c1). Вычтя на графике рис. 11 из ординат кривой η0.л = f(u/c1) ординаты кривой ξт.в = f(u/c1) получают кривую зависимости η0.л = f(u/c1). По этой кривой находят наивыгоднейшее (оптимальна значение отношения (u/c1), соответствующее максимальному значению η0.л 13. По наивыгоднейшему отношению u/c1 производят окончательный расчет, занося все данные в табл. 1. 14. Пользуясь данными, полученными для наивыгоднейшего отношения u/c1, переходят к определению основных размеров проточной части регулирующей ступени. Для этого строят вначале тепловой процесс на диаграмме i — s (рис. 13 вычислив предварительно потери энергии в ступени.) При отсутствии реакции последние рассчитывают по формулам:
или
(потери в соплах);
или
(потери в первом ряду рабочих лопаток);
Рис. 13. Схематическое изображение теплового процесса на i — s-диаграмме для регулирующей ступени турбины
(потери в направляющих лопатках);
(потери во втором ряду рабочих лопаток). С учетом реакции потери определяют по формулам:
или
или
(потери во втором ряду рабочих лопаток);
или
(потери на выходе регулирующей ступени). Относительный к.п.д на лопатках рассчитывают по формуле
и сравнивают со значением, полученным ранее из треугольников скоростей. Отложив на диаграмме i – s (рис. 13) последовательно от точки a1t значения всех потерь, строят тепловой процесс. Точка a1 определяет состояние пара на выходе из сопла, линия A’0a1 характеризует процесс расширения пара в сопле, а точка f1 – состояние пара на выходе из регулирующей ступени. 15. На основании проведенных расчетов и полученных данных, занесенных в табл. 1 для наивыгоднейшего отношения u/c1, а также на основании построенного теплового процесса на диаграмме i – s (рис. 13), определяют основные размеры проточной части регулирующей ступени. В первую очередь выбирают тип сопла.
Рис. 14. радиальный профиль проточной части диска Кертиса. Если отношение p1/p’0>vk (рис. 13), то применяют суживающие сопла; если p1/p’0<vk берут расширяющие сопла, при условии, что косой срез не обеспечивает расширение пара до давления р1 (в противном случае применяют суживающие сопла). Для сухого насыщенного пара vk =0,577, для перегретого vk = 0,546. Суммарную площадь сопел определяют по формулам: в единицах СИ
в единицах системы МКГСС
Здесь G – секундный расход пара, кг/с; p’0 –давление пара перед соплом, бар (кг/см2) v’0 – удельный объем пара перед соплом, м3/кг. Суммарное выходное сечение сопел находят из уравнения неразрывности струи:
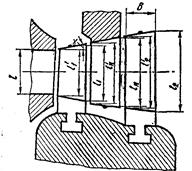
где v1 - удельный объем пара на выходе из сопла в точке а1 на диаграмме i – s (рис. 13). Высоту рабочих лопаток первого ряда на входе l’1 берут на 2 мм больше высоты сопла, т.е. l’1=(l+2)мм, где l - высота сопла (рис.14). Высоту рабочих лопаток первого ряда на выходе определяют по формуле
где c1a и c2a – проекции векторов абсолютных скоростей c1 и с2 на осевое направление, полученные из треугольников скоростей, построенных для наивыгоднейшего отношения u/c1 (рис. 8); v1 и v2 – удельные объемы пара в точках а1и b1, взятые из диаграммы i - s (рис. 13). Высоту направляющих лопаток на входе берут на 2 мм больше высоты рабочих лопаток на выходе:
Высоту направляющих лопаток на выходе определяют по формуле
где с’1а – проекция вектора скорости c’1 на осевое направление, полученная из построенных для наивыгоднейшего отношения u/c1 треугольников скоростей;
Высоту рабочих лопаток на входе второго ряда l’2 берут на 3 мм больше высоты направляющих лопаток на выходе:
а высоту рабочих лопаток на выходе определяют по формуле
где c’2a – проекция вектора скорости c’2 на осевое направление, полученная из треугольников скоростей, построенных для наивыгоднейшего отношения u/с1; v’2 - удельный объем пара в точке d1 , взятый из диаграммы i –s (рис. 13). По полученным размерам вычерчивают радиальный профиль проточной части регулирующей ступени турбины (рис. 14). Иногда этот профиль получается неконструктивным в том смысле, что выходные кромки лопаток чрезмерно увеличены вследствие малых значений с’2а. Это может привести к тому, что струя пара перестанет заполнять «живое» сечение каналов рабочих лопаток, образуются завихрения и увеличатся потери. Для предупреждения завихрений необходимо, чтобы угол γ (рис. 14) не превышал 15-20о. Добиться этого можно путем выбора определенной ширины рабочих лопаток В2 (рис. 22). Если помещенные в атласе профили направляющих и рабочих лопаток удовлетворяют требованиям конструктивного выполнения радиального профиля регулирующей ступени, то на этих профилях можно остановиться. Если же, пользуясь атласом, подобрать профили лопаток не удается, следует воспользоваться заводскими нормалями либо приступить к самостоятельному построению требуемых профилей, руководствуясь методами, изложенными в атласе. Выбор профилей сопловых решеток из атласа начинают с установления того, к какой группе решеток относится рассчитываемая решетка: дозвуковой (А), околозвуковой (Б) или сверхзвуковой (В) (методика определения группы решеток рассматривается в разд. 3.2). Затем из выбранной группы, зная угол наклона сопел а1 (а1эф), выбирают профиль (размер b1 ), удовлетворяющий условию прочности стенки сопловой камеры, на которой крепятся лопатки (рис. 21). Задавшись относительным шагом сопловой решетки t1 = (t1/b1) = 0,7÷0,8 (этим значениям t1 соответствуют минимальные потери энергии), определяют величину шага t1 — t1b1. Зная шаг сопловой решетки, находят число сопел
В том случае, когда число сопел получается дробным, его округляют до ближайшего большего целого числа. Выбор профилей рабочих решеток регулирующей ступени в атласе также начинают с установления того, к какой группе решеток следует отнести рассчитываемую решетку: А, Б или В. Затем из выбранной группы, зная входной угол β1, выбирают профиль (размер b2,), удовлетворяющий условию прочности рабочей лопатки (рис. 22) Задавшись относительным шагом рабочей решетки t2 =t2/b2 таким, чтобы обеспечить минимальные потери энергии в решетке (для этого используют графики, помещенные в атласе; t2=0,5 ÷ 0,75 для всех групп рабочих решеток) из графика β2 = f(t2) путем подбора установочного угла βу находят выходной угол β2эф. Вычислив, шаг рабочей решетки t2 = t2b2, определяют число лопаток
В том случае, когда число рабочих лопаток получается дробным, его округляют до ближайшего меньшего целого числа. Мощность, развиваемую регулирующей ступенью турбины, рассчитывают по формулам: в единицах СИ
в единицах системы МКГСС
Здесь h0 - изоэнтропийный теплоперепад, приходящийся на регулирующую ступень; h0i - внутренний относительный к.п.д. регулирующей ступени. Дата добавления: 2016-03-26 | Просмотры: 1023 | Нарушение авторских прав |
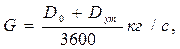
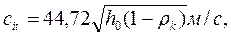
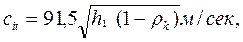
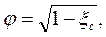

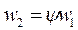
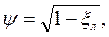
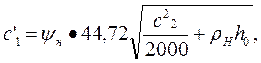
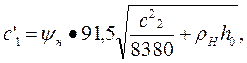
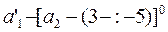
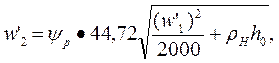
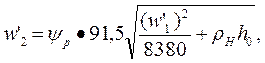
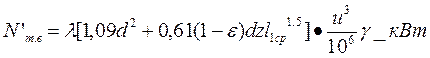
 - средняя высота рабочих лопаток, см;
- средняя высота рабочих лопаток, см; - степень парциальности,
- степень парциальности,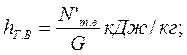
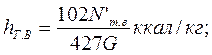
 или
или



 или
или


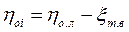
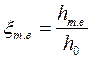
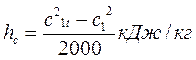
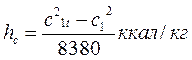
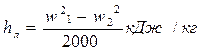
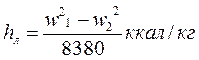
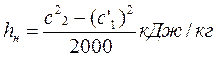
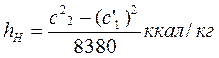
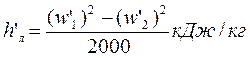
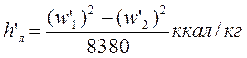
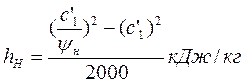
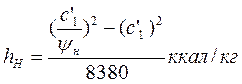
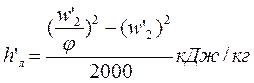
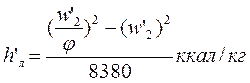
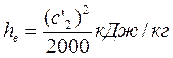
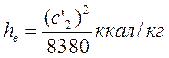
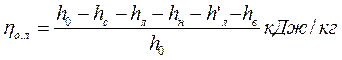
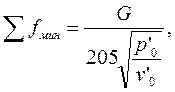
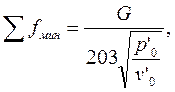
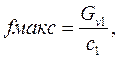
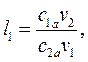
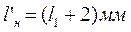
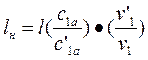
 – удельный объем пара в точке с1, взятый из диаграммы i – s (рис. 13).
– удельный объем пара в точке с1, взятый из диаграммы i – s (рис. 13).