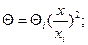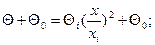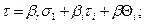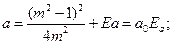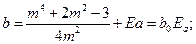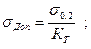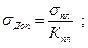АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Определение температурных напряжений в дисках произвольного профиля

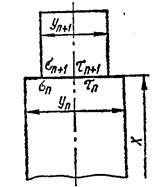
Рис.37. участки постоянной толщины диска.

Вследствие того, что рабочие лопатки диска омываются паром, имеющим высокую температуру, а ступица диска «сидит» на валу турбины, шейки которого охлаждаются смазочным маслом (тем­пература последнего обычно не превышает 60° С), температура различ­ных участков диска будет разной. Закон изменения температуры в диске вдоль радиуса может быть установлен экспериментально; в расчетах же ориентировочно принимают, что температура в дис­ке меняется по закону

где Θ — разность между температурами диска на радиусе х и в цент­ре;

Θ_i, — разность между температурами диска на внутренней поверх­ности расточки ступицы и в центре;

x_t —радиус расточки внутренней поверхности ступицы диска. Поэтому действительная температура диска на радиусе х опреде­ляется выражением

где Θ₀ — действительная температура диска (вала) в его центре.

По этим соотношениям строят кривую изменения температуры в диске вдоль радиуса.

Для расчета температурных напряжений на различных участках диска его профиль заменяют ступенчатым, как это делают при рас­чете динамических напряжений в диске, используя также метод «двух расчетов». Расчет ведут от внутреннего радиуса ступицы к наружному радиусу обода.

Радиальные и тангенциальные температурные напряжения на наружной поверхности первого участка диска рассчитывают по фор­мулам

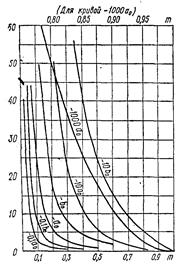
Рис.38. График для определения коэффициентов a₀,b₀ при расчете температурных напряжений в диске постоянной толщины

Здесь σ_t, τ_t — радиальные и тангенциальные температурные напряжения на внутренней поверхности пер­вого участка;

a_r=β _τ и a _τ =β _r — коэффициенты, значения которых определяют точно так же, как и при расчете радиальных и тангенциальных динамических напряжений; а и b — коэффициенты, значения которых определяют так:

где m = x_i/x₁ отношение внутреннего радиуса первого участка диска к наружному радиусу этого же участка.

Для уменьшения вычислений следует воспользоваться графиком, изображенным на рис. 38. Чтобы определить по нему значения коэффициентов а₀ и b_о, нужно из точки на оси абсцисс, соответствующей за­данному т, восстановить перпенди­куляр до пересечения с соответствующими кривыми, и из полученных то­чек опустить перпендикуляры на ось ординат, сделать отсчеты и умножить их на коэффициент, стоящий перед а₀ или b_о на кривой с соответствующим знаком.

В первом расчете на внутренней поверхности первого участка прини­мают σ_i= 0, а τ_i, — произвольным по величине. Используя формулы, рассчитывают а и τ. Для дисков без отверстий радиальные и тангенциаль­ные температурные напряжения в центре диска выбирают произвольны­ми, но одинаковой величины (σ₀ = τ₀).

Напряжения на внутренней по­верхности второго участка определя­ют по формулам для расчета динами­ческих напряжений, приведенным выше.

Переходя от участка к участку, доходят до определения напряже­ний на наружной поверхности последнего участка диска σ_а и τ_а. Если величина σ_а не равна 0, то производят второй расчет для неподвиж­ного диска, нагруженного напряжениями σ_i = 0 и τ_i — произвольным по величине.

Чтобы не делать второго расчета, можно использовать второй расчет при определении динамических напряжений в диске, после чего определить действительные температурные напряжения. Для этого из уравнения σ _а = σ^I_a+kσ^II_a находят значение коэффициента k, на который необходимо умножить температурное напряжение при втором расчете σ^II_a с тем, чтобы, сложив это произведение с напряже­нием при первом расчете σ^I_a, получить действительное радиальное температурное напряжение на наружной поверхности последнего участка диска σ _а= 0. При этом

Рис.39. Динамические и температурные напряжения в диске произвольного профиля.

Данные по расчету коэффициентов, входящих в формулы для опре­деления динамических и температурных напряжений в диске, а также данные по непосредственному расчету этих напряжений заносят в табл. 6, 7. Таблиц 7 составляется две: одна — для динамических, а вторая — для температурных напряжений. Истинные значения динамических и температурных напряжений в диске отображают графически в виде зависимостей σ = f(х) и

τ = f(х), как показано на примере рис. 39. Для изготовления дисков паровых турбин небольшой мощности и работающих при невысоких температурах (до 300° С) применяют сталь марки 45. При более высоких температурах используют стали

перлитного класса следующих марок: 34ХНЗМ (до 400°С), 34ХМ (до 500° С), 25Х1М1Ф (до 540° С) и 20ХЗМВФ (до 560°С). Характе­ристики всех вышеуказанных сталей приведены в табл. 8.

При расчете дисков с температурой металла ниже 430°С крите­рием прочности для перлитных сталей является предел текучести σ_0,2. При более высоких температурах необходимо учитывать также предел длительной прочности σ_дл и предел ползучести σ _пл.

Коэффициенты запаса прочности рекомендуется брать следующие:

К_T = 2,2; K_дл = 1,65; К_пл— 1,25.

Допустимые напряжения соответственно будут:

Допустимым считается минимальное из трех получаемых напря­жений.

Дата добавления: 2016-03-26 | Просмотры: 514 | Нарушение авторских прав