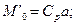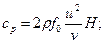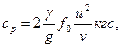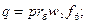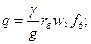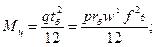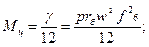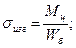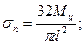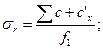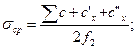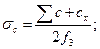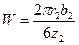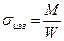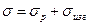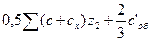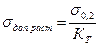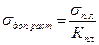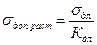АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Изгиб лопатки центробежной силой, приложенной эксцентрично

Если вектор центробежной силы лопатки не пересекает центр тяжести рассматриваемого сечения, то возникает изгибающий момент, равный произведению центробежной силы с_p на эксцентриси­тет этой силы а по отношению к центру тяжести:

Здесь

или

где ρ — плотность материала лопатки, кг/м³;

f0 — площадь сечения профиля лопатки, м²;

ν — отношение среднего диаметра ступени к длине лопатки;

и — окружная скорость на среднем диаметре ступени, м/с;

γ — удельный вес материала лопатки, кг/см⁸;

g = 9,81 м/с² — ускорение земного тяготения.

Этот изгибающий момент складывают с моментом сил действия па­ра (с учетом направления их действия) и получают суммарные изги­бающие напряжения на кромках и спинке лопатки в рассматривае­мом сечении профиля, в том числе и у основания.

5 — 4. Расчет бандажа и шипов лопатки

Центробежная сила собственной массы бандажа или

проволоки действует как изгибающая нагрузка. Часть бандажа между

двумя лопатками можно рассматривать как балку длиной t₆ с жестко

закрепленными концами и с равномерно распределенной нагрузкой

интенсивностью

или

гдеω — угловая скорость вращения;

f_б — площадь поперечного сечения бандажа;

r_б — радиус приложения центра тяжести сечения бандажа. Изгибающий момент за счет центробежной силы в местах закреп­ления бандажа

или

Для скрепляющей проволоки изгибающий момент

где f_п — площадь поперечного сечения проволоки;

t_n — шаг проволоки;

r_п — радиус, на котором расположен центр тяжести сеченияпроволоки.

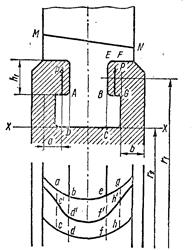
Рис.34. К расчету Т-образного хвостовика рабочих лопаток

Напряжение изгиба в сечении заделки шипом бандажа

где W₆ — момент сопротивления бандажа с учетом ослабления его

отверстием под шип лопатки.

Напряжение изгиба скрепляющей проволоки

где d — диаметр проволоки.

5 — 5. Расчет хвостовика лопаток и ободка диска

Хвостовики рабочих лопаток имеют различную кон­струкцию, но все они подвергаются действию центробежной силы собственных масс, части бандажа и скрепляющей проволоки.

В качестве примера рассмотрим, как рассчитывают Т-образный хвостовик рабочих лопаток (рис. 34).

Наибольшее растягивающее на­пряжение в таком хвостовике возни­кает в сечении АВ. Сумму центро­бежных сил профильной части лопат­ки, бандажей и проволоки, т. е. центробежных сил, развиваемых мас­сами, лежащими над сечением МN, обозначают через ΣС, центробежную силу части хвостовика, ограничен­ной линиями MN и АВ, — через С’_х. Площадь поперечного сечения хвостовика по АВ определяется пло­щадью фигуры befd (или bef'd' для лопаток с отдельной промежуточной вставкой); эту площадь обозначают через f₁. Напряжение разрыва в сечении АВ

Напряжение среза в сечениях AD и ВС хвостовика

где с”_х — центробежная сила участка ABCD (в плане — фигура befd или bef'd' для лопаток с отдельной промежуточной вставкой);

f₂ — площадь среза, равная AD • bd (или AD • bd' для лопаток с отдельной промежуточной вставкой).

На площадках abdc и eghf (или abd'c' и egh'f' для лопаток с отдель­ной промежуточной вставкой) в хвостовике возникает напряжение смятия

где с_х — полная центробежная сила хвостовика между сечениями

MN и хх;

F₃ — площадь фигуры abdc (abd'c') или фигуры eghf (egh'f').

В ободе диска за счет центробежных сил лопаток и самого обода возникают растягивающие и изгибающие напряжения. При расчете пренебрегают кривизной обода диска и рассматривают его как плос­кую балку.

Круговое сечение по хх площадью 4πr₂b нагружено центробежной силой всех лопаток с хвостовиками, т.е. z₂ (ΣC + С_х), и центробеж­ной силой С_об части обода над сечением хх (без хвостовиков лопаток).

Для расчета берут 2/3 С_об, поскольку обод представляет собой кольцо и его центробежная сила вызывает не только радиальные напряжения, но и тангенциальные. Поэтому напряжение в ободе за счет центро­бежных сил будет.

Каждая из двух сил, изгибающих обод в противоположные сторо­ны, является суммой центробежных сил, приходящихся на лопатку:

где С_об — центробежная сила кольца BEFG (рис. 34). Изгибающий момент в сечении хх

М = Ра.