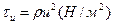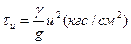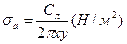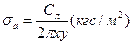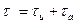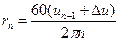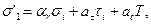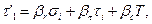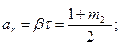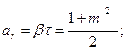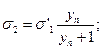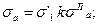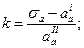АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Определение динамических напряжений

Расчет барабанов. Если толщина барабана намного меньше его диаметра, то такой барабан рассчитывают как свободно вращающееся кольцо. Тангенциальные напряжения, возникающие в барабане за счет центробежной силы его массы, являются функцией скорости вращения барабана и и плотности материала ρ, из которого он изготовлен:

или

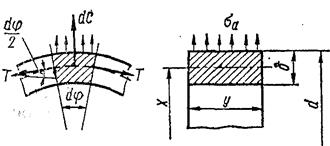
Р ис.35 Напряжения, возникающие в теле барабана.

Так как в теле барабана закреплены рабочие лопатки, то возни­кают дополнительные тангенциальные напряжения τ_а за счет центро­бежных сил собственных масс лопаток и проставных тел.

Предположив, что на 1 см² цилиндрической поверхности барабана вдоль радиуса х (рис. 35) действует центробежная сила С_л, можно записать:

или

Тогда формула для расчета дополнительных тангенциальных напряжений будет:

где δ — толщина стенки барабана.

Суммарные тангенциальные напряжения, возникающие в барабане за счет центробежных сил собственно барабана, лопаток и простав­ных тел,

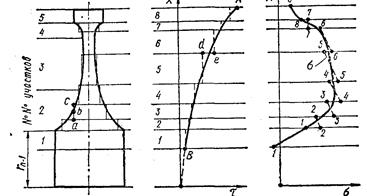
Если толщина барабана большая (δ/d=0,4÷0,47), то такой барабан рассчитывают, используя формулы для диска.

Расчет дисков. При расчете диска турбины любого профиля дан­ный профиль заменяют ступенчатым, составленным из ряда участков постоянной толщины. Число участков выбирают произвольным, но при этом учитывают окружную скорость диска, которая в пределах одного участка не должна превышать 20—30 м/с (при прямолинейном профиле) и 10 м/с (при криволинейном).

Для разбивки диска на участки можно воспользоваться соотноше­нием

где r_п — наружный радиус n-го участка;

u_n-1 — окружная скорость на наружной поверхности предыдуще­го участка радиуса r_n-1 м/с;

Δu — приращение окружной скорости на рассматриваемом уча­стке (Δu = 20÷30 м/с при прямолинейном профиле, Δu = 10 м/с при криволинейном профиле);

п — число оборотов диска, об/мин.

В начале разбивки за r_n-1 следует принять наружный радиус сту­пицы диска (рис. 36).

Выбирая толщину участка в ступенчатом профиле, необходимо сле­дить за тем, чтобы линия истинного профиля пересекала вертикаль­ную линию ступени посредине ее высоты.

Рассчитывают диски по методу «двух расчетов». При этом вычисле­ния можно вести как от внутреннего радиуса ступицы к наружному радиусу обода, так и в обратном направлении.

Для вычислений по первому способу задаются радиальным напря­жением на внутренней поверхности ступицы диска σ_i. При посадке диска на вал с натягом и номинальном числе оборотов ротора берут σ_i = 5÷15 МН/м². Кроме того, на этой же поверхности задаются произвольным значением тангенциального напряжения τ_i. По формулам

рассчитывают радиальные и тангенциальные напряжения на наруж­ной поверхности первого участка (нагружена поверхность ступицы диска).

Рис. 36. К расчету диска произвольного профиля

Коэффициенты α и β, являющиеся функциями отношения радиусов

т = x_i/x₁ (xi,x1 — внутренний и наружный радиусы первого участка), определяют по формулам

Значения коэффициентов а_с и β_с для стальных дисков рассчитывают так:

в единицах СИ

а_с = — 2,74 (3,3 — 2,6/m² — 0,7m⁴),

β_с = — 2,74 (1,9 - 2,6m² — 0,7m⁴);

в единицах системы МКГСС

а_с = — 27,5 (3,3 — 2,6m² — 0,7m⁴),

β_с = — 27,5 (1,9 — 2,6 m ² — 0,7т⁴).

Величина Т =d/1000*n/1000, где d берется в миллиметрах.

Напряжения σ₂ и τ₂ на том же радиусе х₁ второго участка (рис. 37) определяют по формулам

где у_п — ширина первого участка;

у_п+1 — ширина второго участка;

v = 0,3 — коэффициент Пуассона.

Далее находят напряжения σ'₂ и τ'₂ на наружном радиуса второго участка, воспользовавшись формулами, аналогичными формулам для определения напряжений q'₁ и τ'₁ на наружной по­верхности первого участка. При этом величина m будет отношением внутреннего радиуса к наружному радиусу второго участка.

Напряжения σ₃ и τ ₃ на внутренней поверхности третьего участка рассчитывают по формулам

где у_п+2 — ширина третьего участка.

В такой же последовательности определяют на­пряжения на внутренней и наружной поверхностях остальных участков, пока не получат напряжения σ _а и τ _о на наружной поверхности обода диска. Вели­чина напряжения σ_а может не совпасть с действительным напряжением на ободе диска, полученным из расчета хвостовика лопаток и обода диска. Для получения действительных напряжений предполагают, что когда диск находится в покое, в его теле имеются напряжения. Если эти напряжения сложить с напряжениями, получаемыми при вращении диска с номинальным числом оборотов, то суммарные на­пряжения будут действительными напряжениями в диске.

После этого задаются новыми значениями напряжений на внутрен­ней поверхности ступицы диска σ²_i, τ²_i и производят второй расчет, определяя напряжения на внутренних и наружных поверхностях всех участков, в том числе σ¹¹ и τ¹¹ на наружной поверхности обода диска. Эти напряжения также не соответствуют действительным на­пряжениям в диске. Для того чтобы определить их, рассуждают таким образом: на какой коэффициент k. необходимо умножить напряжения σ^II_a с тем, чтобы, сложив это произведение с σ^I_a, получить действитель­ное радиальное напряжение на обеде диска

Решив последнее уравнение относительно k, находят

Умножив все напряжения из второго расчета на коэффициент k и сложив их с напряжениями из первого расчета, получают истинные напряжения на внутренних и наружных поверхностях всех участков диска.

Диск без отверстия (для вала) рассчитывают таким же методом, но принимают, что радиальные и тангенциальные напряжения в центре диска одинаковы, ими и задаются при первом и втором расчетах.

Дата добавления: 2016-03-26 | Просмотры: 477 | Нарушение авторских прав