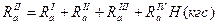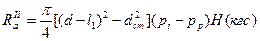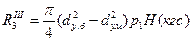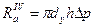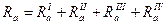|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Расчет последующих ступеней
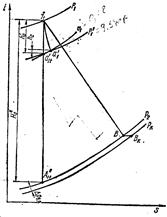
Точка f1 на диаграмме i — s (рис. 1,13) характеризует состояние пара на входе сопел первой ступени, причем она может и не попасть на линию А'оВ. Это может произойти в результате того, что η0i, вычисленный для турбины, может не совпасть с η Oi, рассчитанным для регулирующей ступени. Если из точки f1 (рис. 1) провести изоэнтропу до пересечения ее с изобарой р2 и точку пересечения обозначить A”1t, то отрезок f1 A”1t будет изоэнтропийным теплоперепадом Н”о, приходящимся на остальные ступени турбины. Прежде чем определить число ступеней ираспределить теплоперепад между ними, производят расчет первой и последней ступеней турбины. Расчет первой ступени. Размеры первой ступени должны быть такими, чтобы высота сопел была не меньше 10 мм для фрезерованных и15 мм для залитных лопаток. Диаметр первой ступени определяют по формуле
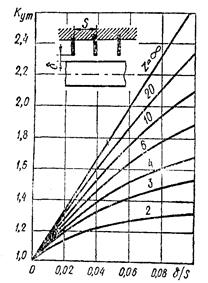
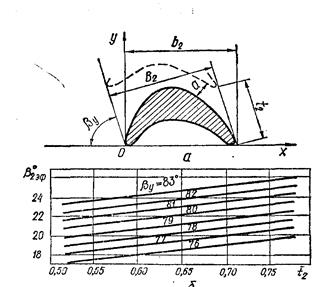
где G — секундный расход пара, кг/с; vi — удельный объем пара на выходе из сопла, м3/кг; х =u/c1 (выбирается в пределах 0,42 — 0,48; большие значения берут для более экономичных турбин) п — число оборотов турбины, об/мин; l — высота сопла, м; μ1— коэффициент расхода в сопловой решетке, определяемый из графика (рис. 12); е > 0,2 — степень парциальности (желательно, чтобы е = 1); а1— угол наклона сопел (выбирается в пределах 11—16° с последующим увеличением до 30—35° в последних ступенях). Задавшись значениями х, l, ε и а1, определяют величину d1 как функцию v1, поскольку v1 неизвестно. Численное значение диаметра d1 получают методом приближений. Для этого задаются каким-либо значением d1 и определяют окружную скорость лопаток
Зная и, рассчитывают действительную скорость пара на выходе из сопла
По величине с1 определяют изоэнтропийный теплоперепад, приходящийся на рассчитываемую ступень, используя формулы: в единицах СИ
в единицах системы МКГСС
а также потерю энергии
или
Откладывая от точки f1 (рис. 15) вниз величину h’о, получают точку а’1t, через которую проводят изобару р’1. Отложив от точки a’1t вверх величину hc, получают точку а’1, характеризующую состояние пара на выходе из сопла. Путем интерполяции определяют удельный объем пара vx в точке а1 . Зная vx, находят диаметр рассчитываемой ступени d1. Если полученный результат совпадает с исходным значением d1, которым задались, то на этом определение диаметра первой ступени заканчивают. В противном случае необходимо задаться новым значением диаметрa d1 и повторять расчет до тех пор, пока численные значения диаметра не совпадут. При этом может оказаться, что размер d1 будет чрезмерно мал и конструктивно невыполним; в этом случае нужно уменьшить степень парциальности е и принять ее такой, чтобы диаметр d1 стал приемлемым.
Рис.15.Схематическое изображение теплового процесса на i – s – диаграмме для ступеней давления. Для того чтобы в случае парциального впуска можно было использовать выходные скорости пара в ступенях турбины следующих за первой, нужно иметь одинаковую степень парциальности, а если это невозможно, — то следует принять ее одинаковой для целой группы ступеней и увеличить до полного впуска пара в последующих группах ступеней. Расчет последней ступени. Диаметр последней ступени определяют по формуле
гдеG — секундный расход пара, кг/с; vB — удельный объем пара на выходе из последней ступени турбины, м3/кг (берется из диаграммы i — s на рис. 15 в точке В); (dz/lz) — отношение среднего диаметра последней ступени к длине лопаток (оно должно быть > 10, в противном случае рабочие лопатки должны иметь переменный профиль); μ2 — коэффициент расхода рабочей решетки, определяемый из графика (рис. 12); £= 0,01÷0,02; H0 — изоэнтропийный теплоперепад, приходящийся на турбину, ккал/кг (рис. 1). Задавшись значением dz/lz, определяют величину оптимального диаметра последней ступени. Если теплоперепад Но выражен в кДж/кг, то
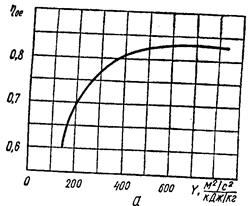
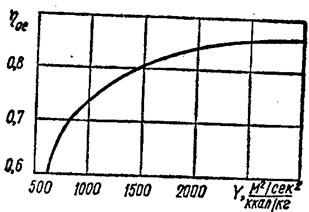
При расчете турбин, работающих с противодавлением, может оказаться, что диаметр последней ступени будет равен диаметру первой ступени или близок к нему. В этом случае диаметры всех ступеней турбины берут одинаковыми. Расчет промежуточных ступеней. Прежде чем приступить к детальному расчету промежуточных ступеней турбины, следует определить число ступеней и распределить теплоперепад между ними. В зависимости от экономичности проектируемой турбины можно по-разному выбирать число ступеней. С увеличением числа ступеней относительный эффективный к. п. д. турбины η0e, как это видно из кривой Парсонса (рис. 16), растет, но турбина при этом будет более сложной в изготовлении и более дорогой. Если важно, в первую очередь, обеспечить простоту конструкции турбины, то ее следует выполнять с ограниченным числом ступеней. Для определения числа ступеней и распределения теплоперепада между ними величину х=u/c1 для всех ступеней принимают постоянной. Изоэнтропийный теплоперепад для любой промежуточной ступени рассчитывают по формулам: в единицах СИ
в единицах системы МКГСС
Рис.16. Зависимость относительного эффективного к.п.д. турбины от коэффициента Парсонса а) в системе СИ; б) в системе МКГСС Здесь с1 – абсолютная скорость пара на выходе из сопла, м/с; Φ=0,095 – скоростной коэффициент сопла. Так как с1= u/x, a u=πdn/60, то
или
При числе оборотов турбины n=3000 об/мин формулы для определения изоэнтропийного теплоперепада в промежуточных ступенях принимают вид: в единицах СИ
в единицах системы МКГСС
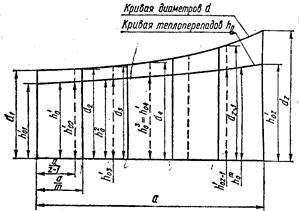
Далее строят вспомогательную диаграмму (рис. 17). Для этого на концах произвольного отрезка прямой а восстанавливают перпендикуляры длиной d1 и dz в любом масштабе и их концы соединяют плавной вогнутой кривой, отображающей изменение диаметров ступеней турбины. В начале кривой рост диаметров незначительный, а затем они увеличиваются более интенсивно. Это объясняется тем, что в начальных ступенях турбины удельный объем пара увеличивается незначительно, а в последующих — растет более интенсивно. Отрезок а делят на т произвольных равных частей. В точках деления восстанавливают перпендикуляры до пересечения с кривой диаметров и получают (т + 1) условных диаметров, для которых, используя последние формулы, определяют изоэнтропийные теплоперепады и строят
Рис. 17. Вспомогательная диаграмма для определения диаметров и теплоперепадов ступеней активной турбины
кривую теплоперепадов h0. Для середины каждого из т участков находят средние значения изоэнтропийных перепадов h’0,h20,h0m-1и т. д., а среднее значение теплоперепада для всей диаграммы рассчитывают так:
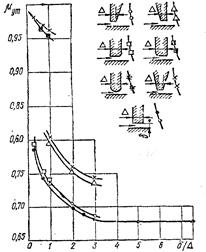
Число ступеней в турбине определяют по формуле
где μ-коэффициент возврата тепла (выбирается в пределах 1,03— 1,08, нижний предел берут для турбин с небольшим числом ступеней, а верхний -для многоступенчатых турбин); Н”о — изоэнтропийный теплоперепад, приходящийся на ступени давления турбины. Полученное значение z округляют до ближайшего целого числа, отрезок а делят на (z — 1) равных частей, а величины теплоперепада и диаметра для каждой из ступеней находят из диаграммы (рис. 17) и заносят в табл. 2.
Сумма всех теплоперепадов, подсчитанная по третьей строке таблицы, может не совпасть с величиной μ H"0. Если расхождение между, последней величиной и так что Распределив теплоперепад между ступенями турбины, приступают к окончательному тепловому расчету ступеней. С этой целью строят треугольники скоростей для каждой ступени с учетом скорости пар на выходе из предыдущей ступени (если эта скорость используется) Зная потери в ступенях, откладывают их на диаграмме i — s и строя тепловой процесс как для отдельных ступеней, так и для всей турбины. После определения размеров проточной части всех ступеней вычерчивают профиль проточной части турбины, следя за тем, чтобы он имел плавные очертания. При наличии резких переходов нужно изменить в соответствующих местах диаметр или выходной угол лопаток. Расчет ступеней давления. По располагаемому изоэнтропийному теплоперепаду на ступень и выбранному скоростному коэффициенту φ определяют скорость выхода пара из сопел с учетом принятой степени реакции r и скорость выхода пара из предыдущей ступени (если эта скорость используется). Задавшись характеристикой ступени давления х и зная абсолютную скорость пара c1, определяют окружную скорость лопаток иуточняют диаметр ступени d. Таблица 2
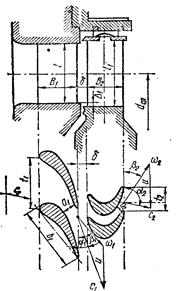
Выбрав угол наклона сопел а1 в пределах, указанных при расчете первой ступени, находят угол направления вектора скорости истечения пара из сопла первой ступени а1 который несколько больше угла а’1 из-за отклонения струи пара косым срезом (при условии, что косой срез расширяет пар до давления, менее критического). По углу а’1, абсолютной с1 и окружной u скоростям строят входной треугольник скоростей, из которого определяют относительную скорость пара на входе лопаток w1 и входной угол β1. Затем строят выходной треугольник скоростей. Для этого находят относительную скорость пара на выходе рабочих лопаток w 3 с учетом степени реакции р, а выходной угол β2 выбирают таким, чтобы после построения выходного треугольника угол a2» » 90°. Определив абсолютную скорость пара на выходе рабочих лопаток с2, по проекциям абсолютных скоростей на направление и(рис. 8) находят относительный к. п. д. на лопатках ηо.л. Определяют потери: в соплах, на рабочих лопатках, выходные, на трение и вентиляцию и на утечку.
Рис. 18. График для определения эмпирического коэффициента расхода пара для уплотнений различной формы Для определения потерь на трение и вентиляцию необходимо знать высоту рабочих лопаток 11 и степень парциальности ε. Для этого, задавшись высотой сопла l и используя формулу, приведенную в п. 12, определяют степень парциальности. Высоту рабочих лопаток находят по формуле
Величину утечки пара рассчитывают по формулам: в единицах СИ
в единицах системы МКГСС
Здесь μут - эмпирический коэффициент расхода, определяемый из графика (рис. 18); FyT — кольцевой минимальный зазор в лабиринтном уплотнении, м2; р0, v0 — параметры пара перед уплотнением, Н/м2(кгс/м2) и м3/кг соответственно;
z — число гребней уплотнения. В случае лабиринтовых уплотнений с гладким валом утечка пара увеличивается и это учитывают поправочным коэффициентом КTу, который определяют из графика (рис 19). Потерю от утечки рассчитывают по формуле
где i0 — энтальпия пара перед уплотнением; i2 — энтальпия пара после рабочего диска с учетом всех потерь, кроме потери на утечку; GyT — секундный расход пара с учетом утечки. Потерю от влажности подсчитывают в ступенях, работающих на влажном паре. Величину этой потери определяют по формуле
где хср — средняя степень сухости пара в ступени; h’i — используемый теплоперепад в ступени с учетом всех потерь, кроме потери от влажности.
Рис. 19. График для определения поправочного коэффициента при расчете лабиринтовых уплотнений с гладким валом После определения всех потерь в ступени на диаграмме i —s откладывают сначала потери в соплах и определяют параметры пара на выходе из сопел рс, vс. Затем откладывают сумму остальных потерь и определяют параметры пара на выходе из рабочих лопаток рр, vp. Скорость звука в среде пара за соплами рассчитывают по формуле
Здесь k — показатель изоэнтропы (для перегретого пара k— 1,3; для насыщенного — k = 1,035 + 0,1 хср, где xсp -средняя степень сухости пара); g = 9,81м/с2; рс,, vc — параметры пара, кг/м2 и м3/кг соответственно. Скорость звука в среде пара за рабочими лопатками находят по формуле
где рр, vp — параметры пара, кг/м2 и м3/кг соответственно. Далее определяют числа Маха Мс1t=c1t/ac, Mw2t=w2t/ap и по ним выбирают профиль сопловой и рабочей решеток из атласа Дейча М. Е. и др. Обозначения профилей в атласе состоят из букв и цифр. Первая буква С, например, указывает, что профиль сопловый и предназначендля сопел активных турбин и для направляющих и рабочих лопатокреактивных турбин. Первая буква Р говорит о том, что профиль предназначен для рабочих решеток активных турбин. Две (или три) первые цифры обозначают входной угол решетки β1 а две последние — выходной угол решетки β2. Последняя буква в обозначении характеризует расчетное число Маха: А — дозвуковые скорости, М < 0,9; Б — околозвуковые скорости, 0,9 < М < 1,2; В — сверхзвуковые скорости, М> 1,2. При выборе профиля сопловой решетки необходимо учитывать, что длина хорды профиля решетки b1должна удовлетворять условиям прочности и жесткости диафрагм (рис. 20, 21). Для активных турбин b1=40÷80 мм (большие значения относятся к первой и последней ступеням турбины).
Рис.20. Проточная часть и профили решеток ступени.
Рис.21. Профиль сопловой решетки (а) и график для определения угла установки сопловой решетки (б) Затем выбирают относительный шаг сопловой решетки t=t1/b1 (t1 — шаг решетки), оптимальные значения которого лежат в пределах 0,7—0,8 (при этом будут минимальные потери в решетке). Величину шага решетки определяют по формуле t1 = t1b1. Длину хорды профиля рабочей решетки b 2 выбирают из условия ее прочности (рис. 22). При выборе профиля рабочих лопаток ориентируются на профили, помещенные в атласе, которые экспериментально проверены в комбинации с сопловыми решетками. В атласе указаны шаг и другие размеры, рабочих лопаток, а также прочностные характеристики профилей лопаток. Выбор профилей сопловых и рабочих решеток, определение их шагов t1 и t2, установочных углов ау и βу, числа сопел z1 и рабочих лопаток z2 осуществляют так же, как и для регулирующей ступени, о чем говорилось выше. Суммируя потери в ступени, определяют используемый теплоперепад, внутренний относительный к. п. д. и мощность ступени. При использовании в ступени скорости выхода пара из предыдущей ступени используемый теплоперепад рассчитывают по формуле
где h0 — располагаемый теплоперёпад; Σh — сумма всех потерь в ступени; h´в— потеря энергии с выходной скоростью и предыдущей ступени. Внутренний относительный к. п. д. ступени определяют по формуле
где Ео = h0 + h'B — располагаемая энергия.
Рис. 22. Профиль активной рабочей решетки (а) и график для определения угла установки рабочей решетки (б) 3 — 3. Определение осевых усилий, действующих На ротор
Пар,расширяясь в проточной части турбины, создает не только окружные усилия, действующие на рабочие лопатки, но и усилия, направленные по ходу пара и стремящиеся сдвинуть ротор в осевом направлении. Последние воспринимаются упорным подшипником. Для расчета упорного подшипника необходимо с достаточно точностью определить эти осевые усилия. Осевое усилие, действующее на венец рабочих лопаток, рассчитывают по формулам: в единицах СИ
в единицах системы МКГСС
Здесь первое слагаемое является динамической составляющей действия пара на рабочий венец, а второе слагаемое — статической составляющей. Если по обе стороны диска давление не одинаково, то осевое усилие, действующее на обод и полотно диска, определяют
по формуле
где dст — диаметр ступицы диска. Если диафрагменные уплотнения, устанавливаемые по обе стороны диска, имеют разные диаметры, то осевое усилие, действующее на торцевую поверхность ступицы диска, находят по формуле
где dу.б — диаметр диафрагменного уплотнения больший; dу.м — диаметр диафрагменного уплотнения меньший; p1— давление пара со стороны меньшего уплотнения. Если в уплотнении ротора выполнены канавки, то возникает осевое усилие из-за неравенства давлений по обе стороны выступа, которое можно рассчитать по формуле
де h — высота выступа в уплотнении; ΔP=0,5(p0-p1) — половина разности давлений по обе стороны диафрагмы. Суммарное осевое усилие, действующее на диск, определяют так:
Суммируя осевые усилия, действующие на все диски, получают усилие ΣRa, стремящееся сдвинуть ротор в осевом направлении. Все данные по расчету первой, последней и промежуточных ступеней турбины, а также по определению осевых усилий, действующих на ее ротор, заносят в табл. 3. Дата добавления: 2016-03-26 | Просмотры: 1002 | Нарушение авторских прав |
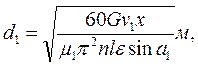
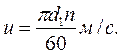
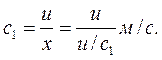
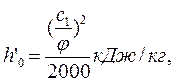
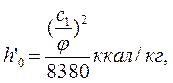
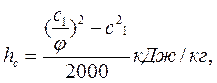
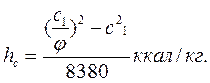
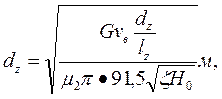
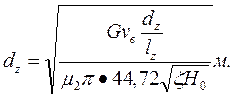
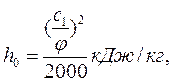
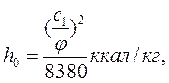
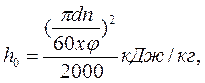
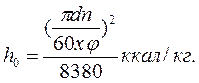

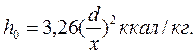
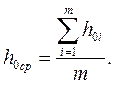
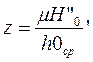
 составит Δ, кДж/кг (или Δ, ккал/кг)
составит Δ, кДж/кг (или Δ, ккал/кг) то величину Δ можно разбить на z ступеней и в четвертую строку таблицы записать окончательно полученные теплоперепады для всех ступеней турбины.
то величину Δ можно разбить на z ступеней и в четвертую строку таблицы записать окончательно полученные теплоперепады для всех ступеней турбины.
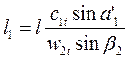
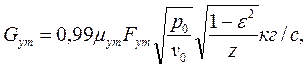
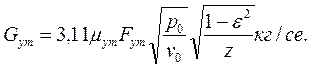
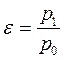 отношение давлений по обе стороны уплотнения
отношение давлений по обе стороны уплотнения
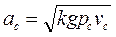
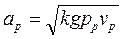

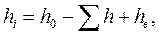
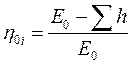
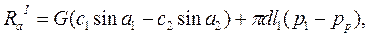
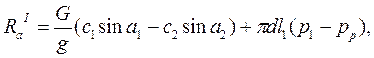

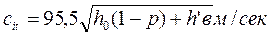
 м/с
м/с
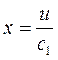
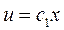 м/с
м/с
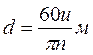
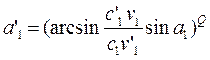
 или
или

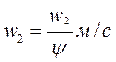

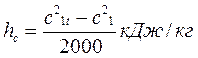 или
или
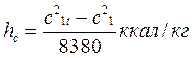
 или
или
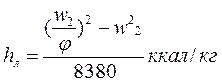
 или
или
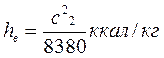

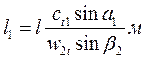

 или
или
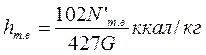

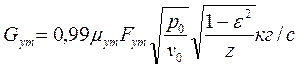 или
или
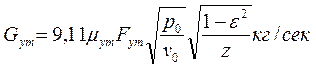
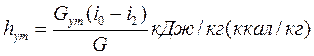


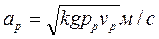



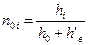
 или
или
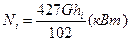
 или
или

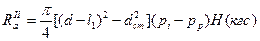 диска,
диска,