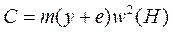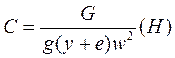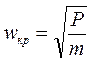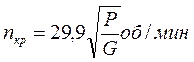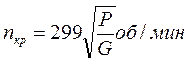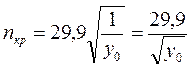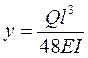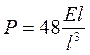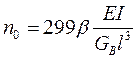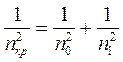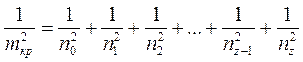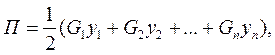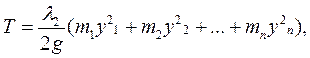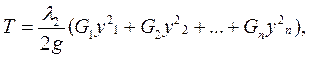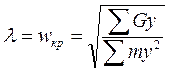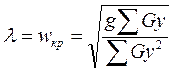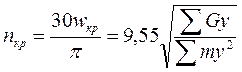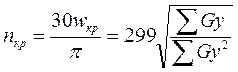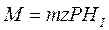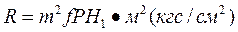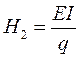АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

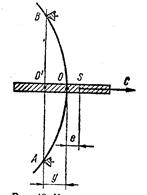
ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОГО ЧИСЛА ОБОРОТОВ РОТОРА

8 — 1. Понятие о критическом числе оборотов

При изготовлении ротора турбины стремятся совмес­тить центр тяжести ротора с геометрической осью вала, т. е. отбалан­сировать ротор, чтобы избежать возникновения центробежных сил, вызывающих колебания ротора. Добиться такого абсолютного совме­щения можно лишь случайно. Но даже при абсолютном совпадении центра тяжести ротора с геометрической осью вала из-за прогиба вала под действием собственного веса и веса насаженных на него дис­ков такое совпадение нарушается, и это приводит к колебаниям ро­тора.

Под критическим числом оборотов ротора понимают такое число оборотов, при котором развивающиеся центробежные силы вызывают прогиб вала ротора, равный бесконечности, т. е. разрушают вал.

Найдем критическое число оборотов ротора с одним диском, до­пуская при этом, что вал невесомый.

Величину центробежной силы, действующей на ротор с одним дис­ком (рис. 40), можно определить по формулам:

в единицах СИ

в единицах системы MKTCC

Здесь

m — масса диска, кг;

у — прогиб вала, м (см);

е — эксцентриситет, м (см);

ω=πτ/30 -угловая скорость диска, рад/с;

G — сила тяжести диска, кгс;

g = 981 см/сек² — ускорение земного тяготения.

Если принять С = Ру, где Р — сила в ньютонах (кгс), котораявызывает прогиб вала на 1 м (1 см), то Ру = т(у + е) ω ², откуда y=meω²/P-mω²

Прогиб вала у может быть бесконечно большим при условии, что P-mω²= 0 (условие разрушения вала). Угловую скорость, при которой происходит разрушение, называют кри­тической угловой скоростью ω_кр, а число обо­ротов ротора — критическим числом оборо­тов n_кр.

Из последнего уравнения, решив его отно­сительно критической угловой скорости, можно получить.

Тогда критическое число оборотов

Рис. 40. К расчету кри­тического числа оборо­тов ротора

Подставив в последнее уравнение значение т = G/g, получают

формулы для определения критического числа оборотов ротора:

в единицах СИ

в единицах системы МКГСС

Сила Р вызывает прогиб вала на 1 м (см). При силе тяжести диска

G величина прогиба вала у₀ = G/P. Поэтому критическое число обо­ротов вала

или

Величину прогиба вала, свободно лежащего на двух опорах с диском посредине, определяют по формуле

где l — длина вала, м (см);

Е — модуль упругости материала, Н/м² (кгс/см^г);

I — момент инерции вала, м⁴ (см⁴);

Q — сила тяжести вала, Н (кгс).

При прогибе вала у == 1 м (см) Q = Р и поэтому

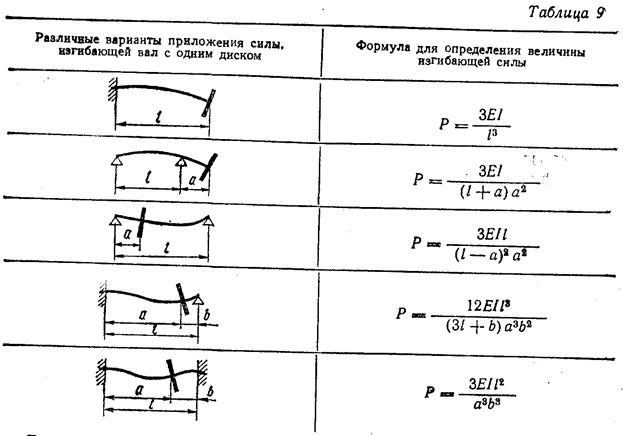
Для иного расположения и выполнения опор и различных точек приложения силы Р ее величину можно определить, используя форму­лы, приведенные в табл. 9.

Зная величину Р и силу тяжести диска G, можно рассчитать кри­тическое число оборотов вала с диском n_кр.

8 — 2. Определение критического числа оборотов вала постоянного диаметра без дисков

Критическое число оборотов собственно вала на основа­нии теории колебаний определяют по формуле

где Е — модуль упругости материала, из которого изготовлен вал,Н/м² (кгс/см²);

I — момент инерции сечения вала, м⁴ (см⁴);

G_B — сила тяжести вала, Н (кгс);

I — расстояние между точками опор вала, м (см);

Р — коэффициент, зависящий от угловой скорости и типа опор вала (выбирается из табл. 10).

Таблица 10

Примечания: 1. Под тоном следует понимать форму упругой линии ва­ла при колебаниях, которая меняется с изменением угловой скорости. Более подробно см. книгу Г. С. Жирицкого «Конструирование и расчет на прочность деталей паровых турбин».

2. Самым опасным является 1-й тон, поскольку при этом величина стрелы прогиба будет максимальной.

8 — 3. Определение критического числа оборотов вала постоянного диаметра с дисками

Для приближенного определения критического числа оборотов вала с диском п_кр (с учетом массы вала) используют формулу

где п₀ — критическое число оборотов собственного вала;

п₁ — критическое число оборотов невесомого вала с диском. Критическое число оборотов вала постоянного диаметра с несколь­кими дисками находят из соотношения

где п₁, п₂,...., п_z-1, п_z — критические числа оборотов вала с одним

первым, одним вторым и т. д. дисками.

8 — 4. Энергетический метод определения критического числа оборотов многодисковых роторов

Этот метод, основанный на равенстве потенциальной и кинетической энергии ротора за период колебаний, применяется в случае ступенчатого вала.

Потенциальная энергия деформации вала, накапливаемая за вре­мя максимального отклонения вала от положения равновесия,

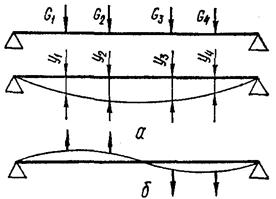
где G₁, G₂,..., G_n — силы тяжести дис­ков и соответству­ющих участков ва­ла;

y₁,y₂,…,y_n - стрелы прогиба ва­ла под соответ­ствующими силами тяжести (рис. 41).

Рис. 41. Схема вала многоступенчатой турбины

Кинетическая энергия ротора за это же время

или

где λ — круговая частота колебаний, равная крити­ческой угловой скорости ротора ω_кр;

т₁, т₂,..., т_п — массы дисков и соответствующих участков вала.

Из условия П = Т можно определить значение круговой частоты:

в единицах СИ

в единицах системы МКГСС

Зная ω_кр, можно рассчитать критическое число оборотов ротора: в единицах СИ

где G [Н], т [кг], у [м];

в единицах системы МКГСС

где G [кгс], у [м];

Рис. 42. Графический метод расчета вала.

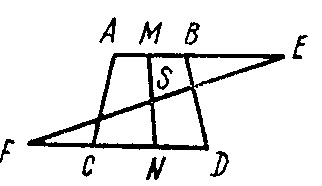
Рис. 43. Определение центра тяжести трапеции.

Из последних формул видно, что для определения п_кр, кроме известных сил тяжести, необходимо знать величины прогиба вала под действием этих сил, т. е. нужно иметь кривую прогиба вала.

Чтобы построить кривую прогиба, удобнее всего воспользоваться графическим методом, применяемым в курсе сопротивления материалов и заключающемся в следующем.

Пусть имеется вал, изображенный на рис. 42, а. Вал состоит из трех участков, диаметры которых d₁, d, d₂, и нагружен четырьмя си­лами G₁, G₂, G₃, G₄.

Вал вычерчивают в масштабе: 1 см == т м (см) натуральной вели­чины, а векторы действующих сил — в масштабе 1 см = Р Н (кгс).

Для определения реакций опор G₅ и G₆, графическим методом, применяемым в курсе теоретической механики, строят:

1) многоугольник сил (рис. 42, б) с полюсным расстоянием Н₁, выбранным произвольно (масштабы сил сохраняют те же, что и на рис. 42, а);

2) веревочный многоугольник (рис. 42, в).

Так как вал под действием реакций G₅, G₆ и сил G₁ —G₄ находится в равновесии, то и многоугольник сил, и веревочный многоугольник должны быть замкнутыми. Имея реакции опор и действующие силы, а также точки их приложения, определяют изгибающие моменты под всеми приложенными к валу силами G₁ —G₄. По полученным изги­бающим моментам строят эпюру изгибающих моментов (рис. 42, г).

Масштаб для построения эпюры выбирают следующим образом. Изгибающий момент в любой точке вала можно найти, умножив соот­ветствующую ординату эпюры z, измеренную в масштабе длин т, на полюсное расстояние Н₁, измеренное в масштабе сил Р:

Приняв z = 1 см, находят, что 1 см чертежа соответствует М = тРН₁ Н·м (кгс). Зная М, по выбранному масштабу строят эпюру изгибающих моментов.

Чтобы учесть непостоянство диаметра вала, один из его участков (с наибольшим диаметром d) принимают за основной, а ординаты эпюры других участков пересчитывают пропорционально отношению моментов инерции сечении вала I/I_x, где I — момент инерции вала с диаметром d, I_x — момент инерции рассматриваемого участка вала. Исходя из этого, на первом участке вала ординаты эпюры изгибающих моментов увеличивают в (d/d₁)⁴

раз, а на третьем участке вала — в(d/d₂)⁴ раз. Таким же образом поступают при учете непостоянства температуры вала, влияющей на ве­личину модуля упругости: взяв для вычислений, модуль Е участка с наибольшим диаметром d, умно­жают ординаты эпюры остальных участков на вели­чину E/E_x, где Е_х — модуль упругости рассматри­ваемого участка при соответствующей температуре.

Для построения упругой линии вала его нужно рассматривать под нагрузкой, измеряемой площадью эпюры изгибающих моментов. Для этого эпюру делят на ряд участков (на рис. 42, г заштрихованы в разные стороны) и в центре тяжести каждого из них прикладывают силу R, равную площади этого участка, выраженную в единицах Н • м³ (кгс/см²). Если площадь рассматриваемого участка в масшта­бе чертежа равна f[см²], то величина изгибающей силы

Участки эпюры изгибающих моментов представляют собой тре­угольники или трапеции (рис. 42, г). Центр тяжести треугольника на­ходится на пересечении медиан. Центр тяжести трапеции определяют графически (рис. 43).

Для этого проводят линию MN, соединяющую середины параллель­ных сторон трапеции, и на продолжении стороны АВ откладывают отрезок BE, равный основанию CD. На продолжении основания DC откладывают отрезок CF, равный основанию АВ. Точки Е и F соеди­няют прямой. Точка пересечения линией EF и MN и есть центр тя­жести трапеции.

Многоугольник сил (рис. 42, д), необходимый для построения кри­вой прогиба, строят в масштабе 1 см == q H • м² (кгс • см²). Полюсное расстояние Н₂ должно равняться EI, а в выбранном масштабе

Эта величина получается слишком большой и для того, чтобы ее можно было отложить на чертеже, ее уменьшают в произвольное (удобное для вычисления) число раз r:

Прогиб вала определяют из кривой прогиба (рис. 42, ё). Величина прогибов на чертеже будет в масштабе 1: m/r. Прогибы вала у ₁ —y₄ берут под точками приложения сил G₁ — G₄. Для определения истин­ных прогибов снятые с рис. 42, е величины нужно умножить на m/r.

Чтобы рассчитать теперь критическое число оборотов ротора, необходимо подсчитать

G₁y₁ + G₂y₂ + G₃y₃ + G_4y4 = Σ Gy