 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Распределенными параметрами
Спектр силы резания и внешних возмущений, вызванных неуравновешенностью заготовки, по данным исследований достигает 100 МГц. Если собственные частоты подвижного люнета и подсистемы инструмента в каждом конкретном случае могут быть приняты стабильными, то жесткость и спектр подсистемы маложесткой детали в связи с изменением положения зоны резания непрерывно меняется, что, в конечном счете, увеличивает вероятность резонанса на высших гармониках. Для реальных нелинейных систем оценить распределение энергии при резонансе по формам колебаний чрезвычайно трудно, поэтому трудно предсказать, какая из собственных форм колебаний окажет наибольшее влияние на поведение систем. Из практики известно, что виброустойчивость такой системы низка, и поэтому мехобработку ведут на очень низких скоростях, т.е. в квазистационарном режиме, что резко снижает производительность и не гарантирует точности мехобработки. С целью повышения производительности и точности мехобработки маложестких деталей необходима разработка эффективных систем управления процессом, синтез которых основывается на современных методах управления технологическими процессами. Расчеты частотных и точностных характеристик процесса мехобработки маложестких деталей базируются на общих закономерностях колебаний сложных механических систем. При этом широко применяется математический аппарат теории автоматического управления и, в частности, рассмотрение задач в комплексной области. Переход в комплексную область позволяет свести динамическую задачу для линейной системы при гармоническом возбуждении к квазистатической с комплексными коэффициентами, зависящими от частоты. Введение комплексных модулей упругости позволяет применить единый подход при рассмотрении вынужденных и собственных колебаний демпфированных и недемпфированных систем. При расчетах сложных механических систем приходится упрощать расчетные модели отдельных деталей и узлов. Эти упрочнения идут по пути линеаризации подсистем и внешних нагрузок, замены гистерезисных потерь колебательной энергии в сочленениях деталей упруго вязкими, рассмотрение части подсистем, как абсолютно жестких и пренебрежения колебаниями по некоторым степеням свободы. Вместе с тем расчет динамических характеристик сложный систем имеет свои специфические задачи: 1. Оптимальное распределение системы на подсистемы. 2. Разработка расчетных моделей подсистем и накопление необходимой для них экспериментальной информации. 3. Создание моделей и алгоритмов расчета, обеспечивающих необходимую точность вычисления и соответствие результатов основным характеристикам реального процесса. 4. Оценка зависимости результатов расчета от точности задания исходной информации. 5. Создание алгоритмов расчета, обеспечивающих минимальное время вычислений на - ЭЦВМ и т.п. С целью разработки системы автоматического управления точностью механической обработки маложестких деталей выделим в качестве объекта управления технологическую систему станка с учетом процесса резания. Из экспериментальных исследований обоснуем следующее разбиение технологической системы на подсистемы: 1. Деталь-опоры. 2. Суппортная группа. 3. Процесс резания. Исследует каждую из подсистем и на базе проведенного анализа объекта управления проведем исследование функциональных и структурных схем автоматического управления точностью мехобработки маложестких деталей. Рассмотрим деталь как однородный стержень, закрепленный в произвольных опорах. Свободные изгибные колебания стержня без действия диссипативных сил описываются уравнением
Когда стержень колеблется по собственным формам колебаний
Подставляя (2.27) в (2.26), получим для собственной формы
где Общее решение (2.28) можно записать в виде
Формы кривых, описывающих прогибы, задаются нормальной функцией
Таким образом, формы колебаний имеют вид синусоид. Применим теперь метод нормальных форм колебаний к исследованию поперечных динамических перемещений стержней. Положим, что на вал действует распределенная поперечная сила N(x, t). В этом случае уравнение движения имеет вид:
Будем искать решение в виде
где Будем изучать устойчивый процесс мехобработки (например, устойчивый процесс резания на токарном станке). Вынужденные колебания детали в плоскости YОХ под действием произвольной гармонической силы
Здесь Пусть к детали, закрепленной в шарнирных опорах, приложена сосредоточенная гармоническая сила
Определим входную передаточную функцию
где Используя (2.36), преобразуем (2.37) к стандартному виду
где Передаточная функция (2.38) реализуется параллельно соединенным звеньям направленного действия. Количество звеньев схемы (число членов ряда 2.38), достаточное для достижения требуемой точности мехобработки, зависит от физических свойств ( Таким образом, передаточная функция подсистемы "деталь-опоры" с распределенными параметрами приводил к сумме нескольких стандартных звеньев с сосредоточенными параметрами, соединенных параллельно. На рис.2.16 приведены АФЧХ подсистемы "деталь-опоры", определенные по формуле при следующих значениях исходных параметров:
Рис.2.16. АФЧХ подсистемы «деталь-опоры» Из построенных АФЧХ следует, что рассматриваемая подсистема является острорезонансной и практически описывается первым слагаемым сумм (2.38). Динамическая характеристика резания как элемента динамической системы станка представляет собой зависимость изменения силы резания от вызвавшего это изменение относительного смещения заготовки и инструмента. Будем использовать динамическую характеристику резания, основанную на анализе полного выражения силы резания. Это выражение силы, резания следует из эмпирических зависимостей и поэтому имеет определенные границы применения: в частности, оно не отражает особенностей замкнутой деформационной системы и ее сложных связей, присущих процессу резания. Однако, выражение силы резания позволяет обнаружить важные закономерности, составляющие основу динамической характеристики, которую можно рассматривать как первое приближение. Динамическая характеристика процесса резания может быть построена только для условий, когда процесс является собственно устойчивым. Для практических расчетов может быть использовано выражение динамической характеристики в форме:
где Постоянные времени При анализе среднечастотной области характеристики в случае обработки с усадкой В случае отсутствия автоколебаний процесс резания целесообразно описать квазистатической характеристикой Этому же соответствует и малость постоянных времени процесса резания по сравнению с постоянной времени упругой системы Теоретический анализ способов обработки нежестких деталей типа "вал-ротор" и анализ динамики системы СПИЗ как объекта управления показали, что одним из эффективных путей повышения точности обработки является разработка систем автоматического управления (САУ) точностью. Потеря точности обработки маложестких деталей вызвана в первую очередь податливостью детали и низкой виброустойчивостью системы СПИЗ в рассматриваемых процессах. Поэтому, естественно, первым вариантом САУ точностью обработки рассматривается САУ положением обрабатываемой детали (и жесткости подсистемы "деталь-опоры") в зоне резания. САУ исследована и реализована как часть комплексной САУ точностью обработки жестких деталей в работах, где доказана работоспособность такой САУ для жестких деталей. Вместе с тем, рассмотренные САУ, компенсируя статистические упругие перемещения, не могут полностью скомпенсировать динамические упругие перемещения нежестких деталей в зоне резания и поэтому не обеспечивают требуемой точности обработки. Можно показать, что высокий уровень динамических усилий (и как следствие, перемещений) в зоне резания вызывается имеющейся всегда неуравновешенностью нежесткой детали. Неуравновешенность детали, состоящая в несовпадении оси вращения с осью инерции, связано с припуском на обработку и его колебаниями, погрешностями предыдущих операций и, особенно, центровочных операций, влиянием веса деталей и др. Важным обстоятельством, обеспечивающим изучение влияния неуравновешенности маложестких деталей на точность обработки является следующее. Любая распределенная по длине вала неуравновешенность может быть разложена на составляющие, каждая из которых соответствует определенной форме упругой линии и вызывает вынужденные колебания только этой формы. Поэтому учет неуравновешенности маложестких деталей можно проводить по собственным формам. Так как частота вынужденных колебаний при обработке нежестких валов, как правило, значительно меньше частоты собственных колебаний подсистемы "деталь-опоры", то для оценки неуравновешенности достаточно учитывать не более трех первых собственных форм, а при определенных условиях достаточно учесть первую собственную форму. Под действием сил инерции и неуравновешенности нежесткий "вал-ротор" в процессе обработки изгибается по пространственной кривой, представляющей наложение гармоник последовательных порядков. Плоскости гармоник, вообще говоря различны. Совокупность плоскостей с лежащими в них гармониками, образует как бы "жесткую" конфигурацию, вращающуюся с валом. При изменении угловой скорости нарушаются соотношения модулей и фаз гармоник. Динамические реакции в опорах и в зоне резания (как было показано выше, воздействие процесса резания на обрабатываемый нежесткий вал может быть заменено при определенных условиях, эквивалентной упругой опорой) можно разбить на слагаемые, соответствующие отдельным гармоникам, лежащие в плоскостях этих гармоник и вращающиеся с угловой скоростью. Модуль амплитуды динамической составляющей можно найти по формуле
где использованы обозначения:
Здесь Анализ формулы показывает, что величина опорных реакций сильно зависит от угловой скорости, ширина диапазонов резонансных колебаний растет с номером Следует заметить, что повышение точности обработки немыслимо без снижения уровня вибраций при резании. Следовательно, ставится вопрос о создании особого класса систем управления, обеспечивающих оптимизацию динамических характеристик системы СПИЗ в процессе резания. При разработке контура управления возникает вопрос о выборе его входного и выходного сигналов. Очевидно, что в задачах, связанных с точностью управления, выходом объекта управления подсистемы "деталь-опоры" должно быть перемещение оси детали и амплитуды колебаний детали относительно принятой базы. Входом же в объект управления могут быть управляющие усилия или управляющие перемещения. На рис.2.17 представлена многоконтурная, многосвязная система управления с тремя точками входа и выхода в объект управления, выходом которого является перемещение оси детали, а входом - управляющее усилие. Связи контуров осуществляются через объект и введенные в рассмотрение передаточные функции объекта управления
Рис.2.17. Структурная схема многоконтурной САУ обработкой длинномерных маложестких заготовок В теоретическом варианте рассматриваемая САУ точностью обработки нежестких деталей в сечении 1 может быть представлена следующими звеньями: датчиком малых перемещений с передаточной функцией Теоретический анализ структурной схемы управления, представленной на рис.2.17, обнаружил следующие недостатки: 1) управляющие усилия Указанных недостатков не имеет схема управления, где входом и выходом в объекте управления являются перемещения оси детали (и амплитуда колебаний детали). Перейдем к анализу такой схемы, представленной на рис.2.18, причем, как следует из сказанного выше, достаточно рассмотреть два канала управления в сечениях 1 и 2. Рассматриваемая система представляет собой двухканальную систему с идентичными каналами. Здесь
Рис.2.18. Структурная схема многоконтурной САУ перемещениями заготовки – двухканальной системы с идентичными каналами
Будем предполагать выполненными необходимые и достаточные условия того, чтобы в системе со связанными между собой через объект управляемыми величинами можно было в каждом контуре управления неограниченно увеличивать коэффициент усиления без нарушения устойчивости в каждом контуре и во всей системе в целом: а) каждая отдельная система без учета взаимовлияния других контуров управления имела структуру, устойчивую при сколь угодно большом коэффициенте усиления; б) вырожденное и вспомогательное уравнения для всей многосвязной системы, каждое в отдельности, удовлетворяли условиям устойчивости. Для повышения устойчивости и качества управления в двухканальных системах получили широкое распространение обратные перекрестные связи между каналами, т.е. связи, имеющие равные, но обратные по знаку, передаточные функции. Обратная связь передает воздействие с выхода одного звена в одном канале на вход идентичного звена в другом канале (связи Прямые перекрестные связи, когда воздействие передается с входа одного звена в одном канале на выход идентичного звена в другом канале, осуществляются самим объектом управления. Комбинация же прямых и обратных связей дает весьма сильный положительный эффект. Далее, исходя из общих усилий устойчивости системы связями через объект управления и того обстоятельства, что контуры управления в рассматриваемой системе образуют друг по отношению к другу отрицательную обратную связь, мы переходим к теоретическому анализу одного канала системы управления приложенного в сечении резания и представленного на рис.2.19.
Рис.2.19. Канал САУ в сечении резания
Здесь на вход объекта управления прикладывается усилие Для анализа такой системы управления составим общую передаточную функцию цепи обратной связи
Передаточная функция объекта с встроенным контуром управления
АФЧХ системы в целом и объекта, рассчитанные при следующих исходных данных: Дата добавления: 2015-01-18 | Просмотры: 991 | Нарушение авторских прав |
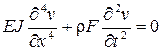 . (2.26)
. (2.26)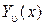 , его прогибы будут изменяться во времени по геометрическому закону
, его прогибы будут изменяться во времени по геометрическому закону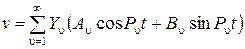 . (2.27)
. (2.27)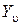 уравнение
уравнение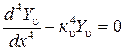 , (2.28)
, (2.28)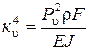 . (2.29)
. (2.29)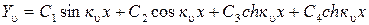 , (2.30)
, (2.30)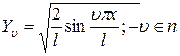 . (2.31)
. (2.31)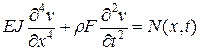 . (2.32)
. (2.32)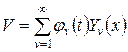 . Используя условия ортогональности и нормируемости собственных функций, получим
. Используя условия ортогональности и нормируемости собственных функций, получим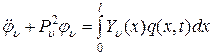 (2.33)
(2.33)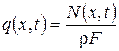 . (2.34)
. (2.34)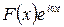 описывается уравнением.
описывается уравнением.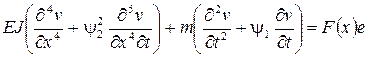 . (3.35)
. (3.35)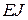 - жесткость при изгибе;
- жесткость при изгибе; 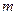 - масса единицы длины детали;
- масса единицы длины детали; 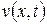 - поперечное смещение;
- поперечное смещение; 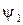 и
и 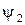 - коэффициенты внешнего и внутреннего трения.
- коэффициенты внешнего и внутреннего трения.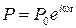 на расстоянии
на расстоянии 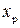 от правой опоры, тогда решение примет вид
от правой опоры, тогда решение примет вид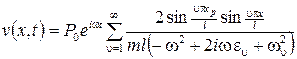 . (2.36)
. (2.36)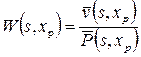 , (2.37)
, (2.37)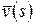 и
и 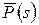 - изображения по Лапласу соответственного перемещения
- изображения по Лапласу соответственного перемещения 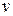 и силы Р.
и силы Р.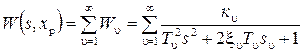 , (2.38)
, (2.38)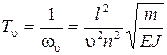 - постоянные времени;
- постоянные времени; 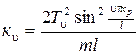 - коэффициенты усиления;
- коэффициенты усиления; 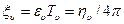 - коэффициенты колебательности (демпфирования);
- коэффициенты колебательности (демпфирования); 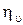 - коэффициент поглощения.
- коэффициент поглощения.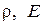 ) и размеров (
) и размеров (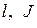 ) детали, а также от близости зон частот вынужденных колебаний и собственных (
) детали, а также от близости зон частот вынужденных колебаний и собственных (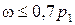 ), то достаточно оставить 2…3 члена.
), то достаточно оставить 2…3 члена.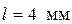 ,
, 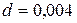 м,
м, 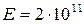 Н/м,
Н/м, 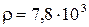 кг/м3.
кг/м3.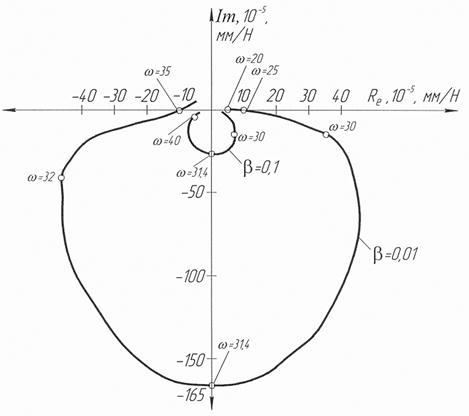
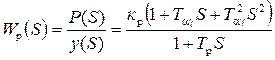 , (2.39)
, (2.39)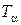 - постоянная времени заднего угла;
- постоянная времени заднего угла; 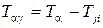 ;
; 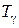 - постоянная времени переднего угла;
- постоянная времени переднего угла; 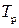 - постоянная времени стружкообразования;
- постоянная времени стружкообразования; 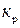 - коэффициент резания, определяемый из выражения
- коэффициент резания, определяемый из выражения 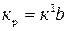 ; где
; где 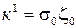 удельная сила резания;
удельная сила резания; 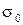 - условное напряжение;
- условное напряжение; 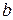 - ширина срезаемого слоя;
- ширина срезаемого слоя; 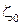 - усадка стружки.
- усадка стружки.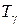 ,
, 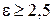 можно пользоваться упрощенным выражением
можно пользоваться упрощенным выражением 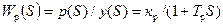 .
.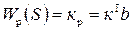 .
.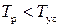 .
.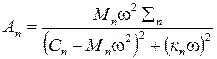 , (2.40)
, (2.40)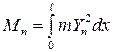 ;
; 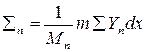 ;
; 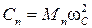 ;
; 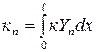 .
.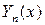 - собственная функция соответствующей недемпфированной системы;
- собственная функция соответствующей недемпфированной системы; 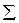 - результирующая неуравновешенность;
- результирующая неуравновешенность; 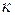 - коэффициент пропорциональности в линейной силе трения.
- коэффициент пропорциональности в линейной силе трения.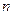 . Поэтому на высших критических скоростях вибрации, как правило, имеют более интенсивный характер, чем на низших, даже несмотря на уменьшение коэффициентов
. Поэтому на высших критических скоростях вибрации, как правило, имеют более интенсивный характер, чем на низших, даже несмотря на уменьшение коэффициентов 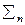 с ростом
с ростом 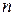 . Из сказанного следует, что для стабилизации процесса резания и, следовательно, повышения точности обработки маложестких деталей надо стабилизировать оси или управлять положением оси вала с целью повышения точности обработки. Таким образом, мы обращаемся ко второму варианту САУ точностью обработки, представляющую многократную систему управления, связанную через объект, которая управляет положением оси и колебаниями детали в точке управления. Количество точек управления и соответственно контуров системы управления, выбирается в зависимости от податливости детали и требуемой точности обработки в статическом режиме.
. Из сказанного следует, что для стабилизации процесса резания и, следовательно, повышения точности обработки маложестких деталей надо стабилизировать оси или управлять положением оси вала с целью повышения точности обработки. Таким образом, мы обращаемся ко второму варианту САУ точностью обработки, представляющую многократную систему управления, связанную через объект, которая управляет положением оси и колебаниями детали в точке управления. Количество точек управления и соответственно контуров системы управления, выбирается в зависимости от податливости детали и требуемой точности обработки в статическом режиме.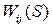 . В сечении 1 на объект действует сила резания
. В сечении 1 на объект действует сила резания 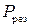 , сила, связанная с неуравновешенностью вала
, сила, связанная с неуравновешенностью вала 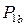 и управляющее усилие
и управляющее усилие 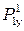 , которые суммируются со своими знаками, образуя силу
, которые суммируются со своими знаками, образуя силу 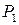 . Сила
. Сила 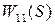 , вызывает смещение оси детали в сечении 1
, вызывает смещение оси детали в сечении 1 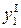 . Результирующие усилия
. Результирующие усилия 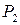 и
и 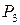 , действующие соответственно в сечениях 2 и 3, вызывают в сечении 1 через передаточные функции
, действующие соответственно в сечениях 2 и 3, вызывают в сечении 1 через передаточные функции 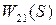 и
и 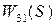 смещение оси
смещение оси 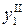 и
и 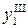 . Полное смещение (или амплитуду колебаний оси детали в сечении 1 получаем сложением слагаемых
. Полное смещение (или амплитуду колебаний оси детали в сечении 1 получаем сложением слагаемых 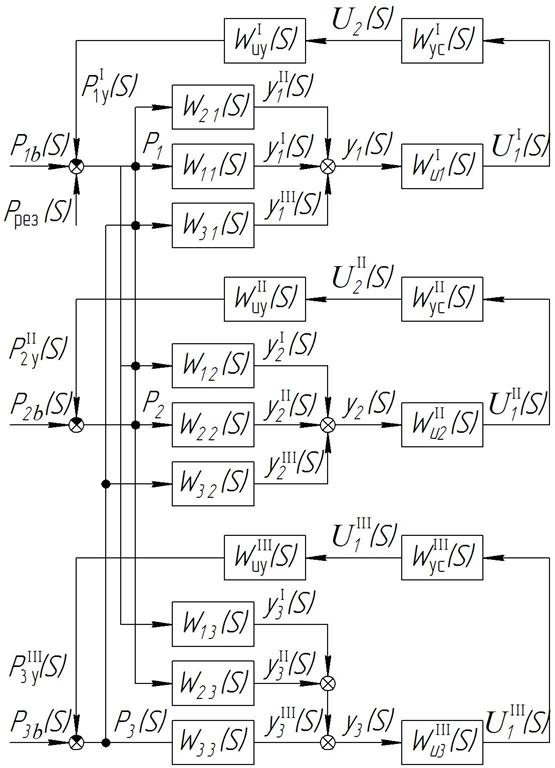
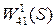 входом которого является перемещение (амплитуда) оси детали в сечении 1
входом которого является перемещение (амплитуда) оси детали в сечении 1 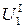 ; усилителя
; усилителя  ; который усиливает сигнал датчика до уровня
; который усиливает сигнал датчика до уровня 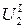 ; исполнительного устройства
; исполнительного устройства 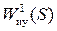 , включенного на выход усилителя и преобразующего его сигнал в управляющее усилие
, включенного на выход усилителя и преобразующего его сигнал в управляющее усилие 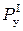 . Аналогично устроены каналы управления в сечениях 2 и 3.
. Аналогично устроены каналы управления в сечениях 2 и 3.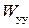 - передаточная функция управляющего устройства в идентичных каналах.
- передаточная функция управляющего устройства в идентичных каналах.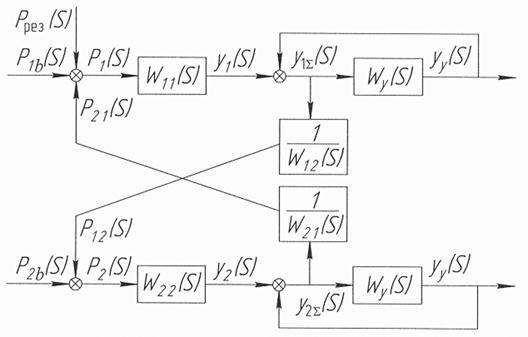
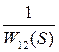 и
и 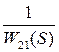 ,
, 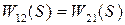 ) рис.2.18.
) рис.2.18.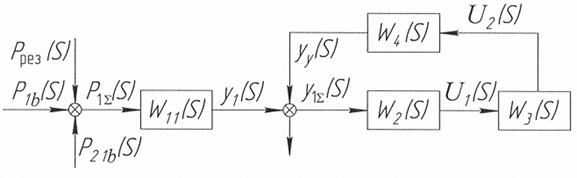
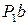 и возмущение, передаваемое с выхода второго канала
и возмущение, передаваемое с выхода второго канала 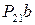 Система управления представлена тремя звеньями: 1) датчиком малых перемещений с передаточной функцией
Система управления представлена тремя звеньями: 1) датчиком малых перемещений с передаточной функцией 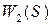 , выходом которого является напряжение
, выходом которого является напряжение 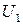 ; 2) усилителем
; 2) усилителем 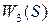 , который усиливает сигнал
, который усиливает сигнал 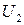 ; 3) исполнительного механизма
; 3) исполнительного механизма 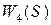 , который преобразует сигнал
, который преобразует сигнал 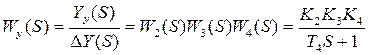 . (2.41)
. (2.41)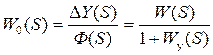 . (2.42)
. (2.42)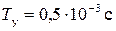 ;
; 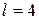 м;
м; 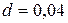 м;
м;