 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Технологической системы при механической обработке
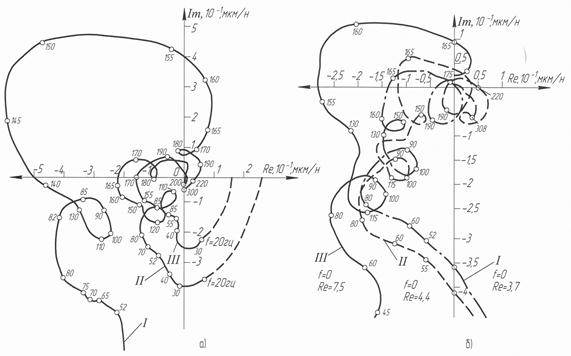
Для синтеза САУ уровнем вибраций и упругими перемещениями в процессе резания необходимо располагать математическим описанием системы СПИЗ как объекта управления. Для проведения математического описания объекта управления - системы СПИЗ токарного станка - на первом этапе исследования необходимо выявить узлы, наиболее существенно влияющие на уровень вибраций, а также принять исходную модель. Задача исследования - анализ известных моделей УС токарных станков, выбор одной из них, наиболее приемлемой для целей математического описания объекта, ее качественная идентификация путем экспериментального изучения и, наконец, опытная оценка допустимости использования линейной модели. Как правило, рассматривается одна из подсистем "деталь-опоры" - ПДО или "резец-суппорт" - ПРС в одной или двух координатной системе. В том и другом случае процесс резания заменялся внешней силой, изменяющейся по синусоидальному закону или учитывался как линейная функция. Целью создания таких моделей явилось теоретическое определение собственных частот элементов УС, либо частот колебаний системы. Для решения указанной задачи были экспериментально получены АФЧХ УС станка модели 1A616. Характеристики представлены на рис.2.1. При снятии АФЧХ деталь зажималась в трехкулачковом патроне (расположение кулачков строго фиксировалось) и прижималась вращающимся центром с постоянным вылетом пиноли l п=25 мм. Деталь имела следующие параметры: диаметр - 54 мм и 85 мм, длину l д=450 мм. Входное и выходное в воздействие регистрировалось по оси Y. Применительно к токарным станкам вибрации и статические перемещения в этом направлении оказывают наибольшее влияние на точность, форму обрабатываемых деталей, чистоту поверхности. Это следует из опыта исследовательской работы в лаборатории ТолПИ и работ других ученых. АФЧХ снимались в зависимости от точки приложения силы по длине заготовки и от жесткости задней бабки, что позволило наиболее полно проанализировать УС станка. На рис.2.1, а представлены экспериментальные АФЧХ в зависимости от точки приложения входного воздействия. Первый годограф снят у задней бабки, второй - в середине детали, третий - у шпинделя (диаметр детали 85 мм). На рис.2.1, б представлены АФЧХ как функции жесткости задней бабки. Первый годограф снят, когда деталь жестко закреплена, второй годограф снят с незакрепленной пинолью, третий - без поджатия задним центром. Из рассмотрения АФЧХ следует, что в формировании амплитуды относительных колебаний - АОК в основном участвуют узлы-массы с собственными частотами 80 Гц и 150 Гц. Для выявления указанных узлов было проведено дополнительное экспериментальное исследование. При этом методом импульсных нагрузок определялись для отдельных элементов собственные частоты. Последние оказались равными для ПДО f =150 Гц, ПРС f = 80 Гц, что соответствует петлям на подографе. Это указывает на ведущую роль данных подсистем в формировании движений инструмента и заготовки. Попутно была проведена оценка влияния этих узлов на динамику процесса резания. Осциллограммы АОК показали, что упомянутые частоты в наибольшей мере влияют на амплитуду формообразующих узлов при резании. Соответственно принятая модель может быть использована при математическом описании объекта управления - системы СПИЗ.
Рис. 2.1. АФЧX технологической системы СПИЗ токарного станка: а – АФЧХ в зависимости от зоны входного воздействия; б – АФЧХ в функции жесткости задней бабки
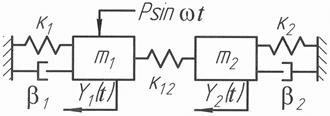
Таким образом, результаты проведенного исследования показали, что УС токарных станков могут с удовлетворительным приближением рассматриваться как двухмассовые при l / d £5,0. При этом жесткость системы СПИЗ и изменение точки приложения основного возмущающего воздействия качественно не меняют характера кривых АФЧХ. Соответственно использование двухмассовой модели для цепей анализа и синтеза остается правомерным во всем диапазоне изменения параметров системы. Это весьма существенно для изучения, реализации и функционирования САУ. Экспериментально показана допустимость (в диапазоне действующих возмущающих) рассмотрения принятой модели в линейной постановке. Кроме то того, проведенное исследование (АФЧХ) показало, что УС может быть представлена в виде комплекса динамических звеньев, доведение которых удовлетворительно описывается уравнениями, как минимум, второго порядка. Полученные результаты позволяют перейти к построению специфической модели системы СПИЗ и ее математическому описанию. С целью выявления доминирующих сил, действующих на СПИЗ, были проведены специальные исследования, при которых на токарном станке модели 1A616 предварительно обрабатывалась заготовка (диаметром 85 мм, длиной 450 мм), которая закреплялась в трехкулачковом патроне и поджималась вращающимся центром, с вылетом пиноли 25 мм. АОК регистрировалась датчиком малых перемещений, который жестко крепился на державке резца и был установлен на 400 мм от шпинделя. Анализируя полученные данные, можно сделать вывод, что основным внешним силовым воздействием является периодическая сила от неуравновешенности вращающейся детали, изменяющаяся по синусоидальному закону. Влиянием остальных внешних воздействий можно пренебречь, они в 8…10 раз меньше. Следует отметить, что хотя УС токарных станков представляет собой многомассовую многосвязную систему, нарушение формы при обработке деталей зависит от главных формообразующих узлов: "деталь-опоры" и "резец-суппорт". Вторая группа сил, порождаемая процессом резания, зависит от многих факторов: режимов резания, геометрии инструмента, материала заготовки и т.д. В случае отсутствия автоколебаний (устойчивом процессе резания, а при этих условиях), процесс резания целесообразно описать квазистатической характеристикой. Этому же соответствует и малость постоянных времени процесса резания по сравнению с постоянными времени упругой системы (T рез< Т ус). Следует отметить, что такая характеристика процесса резания приемлема для решения вопроса об управлении только вынужденными колебаниями, когда УС и процесс резания являются собственно устойчивыми элементами замкнутой системы СПИЗ. Ниже рассматривается модель, учитывающая взаимное влияние основных формообразующих узлов, процесс резания и внешних силовых воздействий на систему. Модель (рис.2.2) представляет собой две сосредоточенные массы m 1, и m 2, закрепленные с неподвижным основанием с помощью пружин и демпферов (с линейными характеристиками и коэффициентами: жесткости к 1, к 2 и демпфирования b1, b2). Взаимное влияние масс осуществляется за счет процесса резания, который описан линейной характеристикой (с коэффициентом жесткости резания к 12). В этом случае амплитуды колебаний резца и детали взаимодействуют друг с другом через процесс резания. Следовательно, амплитуда колебаний детали является функцией амплитуды колебаний резца и изменяется в зависимости от условий протекания процесса резания. Это позволяет считает систему СПИЗ как замкнутую систему. Такая модель принята на основе экспериментальных данных. Приведенная модель описывается системой неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
Здесь
Рис. 2.2. Механическая модель системы СПИЗ с сосредоточенными параметрами
Анализ принятой модели показывает, что формообразующие узлы взаимодействуют между собой через процесс резания. При этом амплитуды колебаний каждой подсистемы представляют собой замкнутый контур, поведение которых зависит от динамических характеристик процесса резания. Последнее накладывает ряд специфических особенностей на поведение системы СПИЗ, в частности, существенно проявляется взаимное влияние отдельных элементов - узлов. Его учет весьма важен для решения поставленной задачи. Решение системы (2.1) позволит исследовать влияние параметров модели на ее поведение. Указанное в дальнейшем дает возможность принципиально обосновать метод минимизации AOK посредством автоматического изменения - подбора параметров системы СПИЗ. Введем новые переменные
Разделим правые и левые части уравнений (2.1) на m 1, и m 2 соответственно
Решаем совместно первое и второе уравнение системы (2.2). Группируем постоянные коэффициенты относительно новых переменных. Вводим обозначения
Получим
Решение ищем в виде
где Подставляя полученное решение в систему (2.3), дифференцируя по х 1 и сократив на
Определитель системы имеет вид
при Используя правило Крамера, находим
Где
при Обозначим
Уравнение (2.6) имеет вид
Ищем решение в виде где Выразим z 0 через постоянные коэффициенты
Введем обозначения:
Часто в системе СПИЗ демпфирование ничтожно мало. Кроме того, это может быть достигнуто специальными конструктивными мероприятиями или на стадии проектирования станка. Для данного случая, (полагая в (2.8) d = 0), имеем
Исследуем полученное решение. Дифференцируем правую часть (2.60) по l2; одновременно числитель приравниваем к нулю
Корни уравнения l12 и l22 отыщем при условии тогда
Очевидно, что решение (2.11) справедливо при
Специально проведенный анализ полученного решения показал, что при наличии демпфирования в системе отсутствие АОК можно достичь только путем одновременного изменения (подбора) как жесткости, так и демпфирования. Управление только жесткостью не позволяет полностью устранить указанные колебания. В то же время последние могут быть существенно снижены. Совместное регулирование жесткости и демпфирования значительно усложнит структуру ж соответственно реализацию, а так же внедрение САУ. Отмеченное делает целесообразным проведение специального исследования. Его цель - выявление принципиально достижимых показателей качества - степени минимизации вибраций в условиях автоматического изменения только жесткости системы СПИЗ. Известно, и др., что снижение уровня вынужденных колебаний на металлорежущих станках обычно достигается изменением параметров системы СПИЗ. При этом обеспечивается "уход" (отстройка) от резонанса. Одной из задач настоящей работы - исследование возможности АОК снижения путем автоматического изменения параметров упругой системы. В предыдущем параграфе отмечалось, что достичь этого путем изменения только жесткости системы СПИЗ невозможно. Ниже расчетно-экспериментальным методом исследуется влияние демпфирования реальных УС токарных станков на амплитуду указанных колебаний и достижимый уровень их минимизации посредством изменения жесткости. При этом используются (2.1) и (2.9). Для численного анализа (2.9) необходимо располагать значениям коэффициентов (2.1) – m 2, к, b, к 12, Р 0. Их величины отыскивались в эксперименте и расчетом, применительно к станку модели 1A616. При этом использовались полученные опытным путем АЧХ и временные характеристики. Усредненные значения постоянных коэффициентов приведены в таблице 2.1. 2.1. Значения коэффициентов формообразующих узлов
Следует отметить, что принятые в расчетах собственные частоты приведенных масс в зависимости от точки приложения возмущающего воздействия, геометрических параметров детали и технологического состояния системы СПИЗ отклонялись от средних на 3…6 %. Это позволяет считать приемлемой точность полученных результатов. В принятой модели системы СПИЗ возмущающая сила представлена в виде явной функции времени. Соответственно она приложена к формообразующим узлам, поведение которых на нее не влияет. И далее, в расчетной схеме внешнее воздействие выражено через силу. Ее составляющая по оси у определяется Штрихпунктирными линиями на тех же рисунках для аналогичных условий дано решение (2.8). Как видно, характер зависимостей остается прежним, но "веер" кривых эквидистантно смещается в сторону увеличения х 1. Отсюда следует, что при наличии в системе затухания путем изменения жесткости может быть достигнут глубокий минимум АОК. Однако добиться их полного устранения невозможно. Последнее является следствием того, что порождаемый демпфированием фазовый сдвиг движении инструмента и заготовки только изменением жесткости системы СПИЗ не устраняется. Здесь для обеспечения минимума АОК необходимо дополнительное управление демпфированием. Дальнейший анализ приводит к выводу о целесообразности использования для значительного класса рассматриваемых систем управления демпфированием и жесткостью. При этом имеет место существенное (приемлемое для технологической практики) снижение х 1. Так, например, для станков токарной группы указанный параметр может быть уменьшен в 10…15 раз и доведен до 2…5 мкм. Это практически не снижает точности формообразования (макрогеометрии детали и чистоты поверхности) и удовлетворяет самым высоким нормам точности.
Рис. 2.3. Графики численного решения уравнений: а, б, в – амплитуды относительных колебаний инструмента и заготовки в функции оборотов шпинделя Обращает на себя внимание падение х 1 с увеличением жесткости резания к12. Это позволяет предположить о наличии, резерва повышения производительности станка и качества обработки изделия. Указанный вопрос выходит за рамки настоящего исследования и в данной работе специально не рассматривается. Таким образом, глубокий минимум AOK достигается только при равенстве частот возмущающей силы (круговой частоты вращающейся детали) и собственной ПРС. Последняя является функцией жесткости и демпфирования. Соответственно путем их подбора или автоматического изменения можно устранить указанные колебания и тем самым повысить точность обработки. Поскольку составляющая х 1, обусловленная демпфированием, порождающий фазовый сдвиг перемещений инструмента и заготовки, относительно мала, поскольку указанную процедуру целесообразно проводить только изменением жесткости. Очевидно, что полученные результаты могут быть использованы применительно к станкам, системы СПИЗ которых могут с достаточным приближением аппроксимироваться принятой моделью. При резании соответствующее изменение параметров УС позволяет получить минимум АОК. При этом осуществляется оптимальный (по минимуму вибраций) подбор параметров системы СПИЗ. Анализ численного решения системы (2.1) показал, что в его практической реализации существуют определенные сложности. Так, например, на современных малообрабатывающих станках с фиксированными параметрами системы СПИЗ, у которых скорость вращения шпинделей не превышает 3.103…6.103 об/мин, на высокопроизводительных режимах обработки, практически невозможно получить точное изделие. Это обусловлено тем, что приведенная частота ПРС не может быть равна частоте внешнего воздействия. Кроме того, технологическая жесткость указанной группы при тех же условиях резко понижается, что способствует снижению ее собственной частоты. Отмеченные затруднения могут быть успешно преодолены введением контуров управления в систему СПИЗ. Для синтеза систем автоматического управления АОК необходимо располагать аналитическими зависимостями с допустимой достоверностью описывающими поведение объекта управления системы СПИЗ с учетом процесса резания. Это требует проведения дополнительного анализа физической картины процессов, разработки (на его основе) динамической структуры, математического описания ее отдельных звеньев и ряда других вопросов. Как отмечалось ранее, основным возмущением в рассматриваемой системе принята сила неуравновешенности Р. Последняя, воздействуя на деталь в процессе резания, характеризующимся коэффициентом к 12, порождает ее перемещение Дальнейший анализ физики явлений, протекающих в системе СПИЗ при резании, обнаруживает существование второго контура преобразований. В частности, отмеченное выше Приведенная трактовка поведения системы позволяет представить динамическую структуру объекта управления в виде, показанном на рис.2.4. Здесь обозначены передаточные функции: W 1(S) - преобразования возмущающей силы Р (S) в одну из составляющих
Рис. 2.4. Структурная схема СПИЗ – модели с сосредоточенными параметрами
Как показывает анализ приведенной динамической структуры, система СПИЗ в условиях принятой модели включает в себя две параллельные ветви, каждая из которых охвачена положительной обратной связью. Очевидно, что в процессе математического описания отдельных звеньев структуры второстепенные связи между ПРС, ПДО и процессом резания должны быть отражены в получаемых выражениях путем ввода параметров одной подсистемы в зависимости, описывающие поведение другой. Для систем управления, обладающих заданными показателями качества, необходимо располагать динамическими характеристиками объекта и аналитическими зависимостями, описывающими его поведение. С этой целью используется ранее приведенный анализ системы СПИЗ с учетом процесса резания. Отыскивается ее передаточная функция как объекта управления и разрабатывается динамическая структура. Поведение объекта можно описать системой линейных неоднородных дифференциальных уравнений. Соответственно (2.1) запишем в операторной форме
Введем обозначения:
Тогда (2.63) примет вид
Из (2.13) применительно к структуре рис. 2.4, а передаточные функции по возмещению (нагрузке), связывающие внешнее силовое воздействие с выходными параметрами
Для оценки влияний движения ПДО и ПРС на формирование относительных колебаний инструмента и заготовки целесообразно располагать соответствующими передаточными функциями (согласно структурной схеме рис. 2.4, а).
И, окончательно, системы СПИЗ в целом
В передаточные функции Такая структура позволяет по-новому рассмотреть динамику процессов, протекающих в станках при резании. В отличии от одномассовых моделей (в которых не вскрывается влияние друг на друга главных формообразующих узлов, а процесс резания вынесен отдельным звеном) в полученной структуре хорошо прослеживается влияние каждого параметра УС и процесса резания на статику и динамику подсистем ПРС и ПДО. В то же время учтена взаимосвязь УС и процесса резания. Как видно из рассмотренного, сила резания зависит от двух переменных 2.2. Значения постоянных времени и коэффициентов усиления
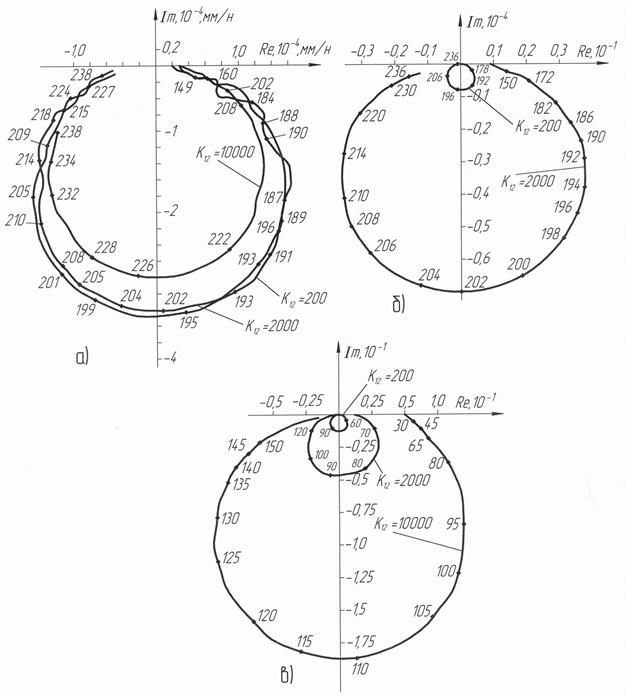
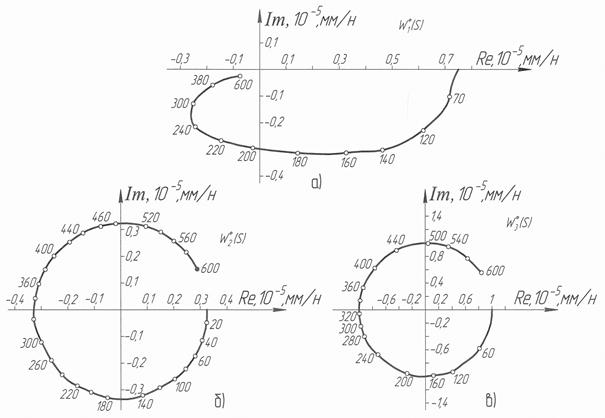
Рис. 2.5. Годографы передаточных функций объекта управления в зависимости от коэффициента связи к 12: а, б, в – АФЧХ звеньев с передаточными функциями W 1(S), W 2(S), W 3(S) соответственно
На рис.2.5, а приведены АФЧХ звена с передаточной функцией Таким образом, увеличение глубины резания, подачи и прочностных характеристик материала приводит к уменьшению составляющих амплитуды колебаний детали, порождаемых процессом, резания. При тех же условиях обработки колебания резцовой группы многократно возрастают, а передача движения от нее к детали так же увеличивается, что показывает чрезвычайную сложность процессов, протекающих в анализируемой системе, даже при упрощающих допущениях принятой модели. Все три звена по своему характеру колебательные и их характеристики не пересекают отрицательную действительную ось. Причем, с увеличением частоты радиус-вектор годографа стремится к нулю. Зависимости выходных координат Заметим, что при возрастании коэффициента связи к 12 собственно частоты ПДО и ПРС повышаются по сравнению с аналогичными частотами отдельно взятого элемента. Эти выводы соответствуют результатам аналитических исследований, проведенных ранее.
Рис. 2.6. Годографы передаточных функций объекта управления: а, б – АФЧХ звеньев с передаточными функциями W 4(S), W 5(S) соответственно
Ранее объект описывался при условии линейности процесса резания. Это вполне допустило при квазистатическом режиме, т.е. когда указанный процесс собственно устойчив. Между тем, при определенных режимах (с учетом свойств обрабатываемого материала и технологического состояния системы СПИЗ) он является нелинейным. При этом автоколебания объясняются тем, что процесс резания и упругая система образуют замкнутый контур, в котором определяющую роль играет упомянутая нелинейность. Ранее задача повышения неустойчивости решалась методом параметрического синтеза (подбора глубины и скорости резания, оптимальной геометрии инструмента, выбором его правильной ориентации и т.д.). Такая постановка не всегда с достаточной полнотой решает задачу повышения производительности и экономического эффекта. Одним из продуктивных путей преодоления возникающих затруднений является введение контура управления. Следует отметить, что в последние годы появились работы, где теоретически (на одномассовой модели) доказана эффективность такого подхода. Проанализируем объект в зависимости от изменения параметров процесса резания. Как показали исследования сила резания отстает по фазе от изменения толщины срезаемого слоя. Принимая это явление за основу и представляя его в виде запаздывания (
где t - время запаздывания. Запишем (2.3) в оперативном виде, вводя следующие обозначения:
Численные значения постоянных коэффициентов в (2.18) применительно к станку модели 1A616: На основе анализа модели с учетом запаздывания динамическую структуру объекта представим в виде, показанном на рис.2.7. Согласно уравнениям (2.18) запишем передаточные функции звеньев
Рис. 2.7. Структурная схема СПИЗ
Полученная структурная схема позволяет вскрыть зависимость выходных координат объекта
Преобразуем структуру рис.2.7 к виду, удобному для анализа устойчивости, рис.2.8. Из ее рассмотрения видно, что устойчивость объекта определяется замкнутым контуром, которой состоит из двух звеньев с передаточными функциями
Рис. 2.8. Структурная схема СПИЗ
АФЧХ, построенные по передаточным функциям
Рис. 2.9. Годографы технологической системы с нелинейным процессом резания: а, б, в – АФЧХ передаточных функций
Анализ полученных АФЧХ показывает, что годографы смещаются во вторую и первую четверть, относительно аналогичных характеристик рис.2.5. С ростом частоты и времени запаздывания фазовый сдвиг выходной величины относительно входной растет, что существенно сказывается на устойчивости объекта управления. Годограф разомкнутого контура Амплитуда относительных колебаний инструмента и заготовки уменьшается по мере роста коэффициента жесткости резаная. Однако, при этом увеличивается постоянная составляющая силы резания, что существенно снижает точность формы обрабатываемой детали. Отсюда следует, что достижение точности обработки при высокой производительности станка может быть получено при введении САУ и, в частности, автоматического управления положением вершины резца и стабилизации положения оси детали.
Дата добавления: 2015-01-18 | Просмотры: 1690 | Нарушение авторских прав |
 (2.1)
(2.1)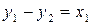 относительное перемещение детали и резца (изменение толщины срезаемого слоя); P (t); P1 (t); Р2 (t) - периодические силы, действующие вследствие неуравновешенности вращающейся детали, передаваемые фундаментом в систему и переменные резания, вызванные неоднородностью материала заготовки, изменениями величины припуска, неравномерностью движения узла. Заметим, что
относительное перемещение детали и резца (изменение толщины срезаемого слоя); P (t); P1 (t); Р2 (t) - периодические силы, действующие вследствие неуравновешенности вращающейся детали, передаваемые фундаментом в систему и переменные резания, вызванные неоднородностью материала заготовки, изменениями величины припуска, неравномерностью движения узла. Заметим, что  - может рассматриваться как квазистатическая характеристика процесса резания. В качестве основного внешнего воздействия принята P (t)изменяющаяся по синусоидальному закону
- может рассматриваться как квазистатическая характеристика процесса резания. В качестве основного внешнего воздействия принята P (t)изменяющаяся по синусоидальному закону  .
.
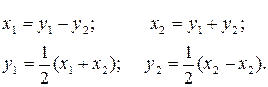
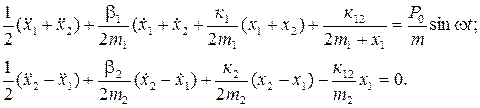 (2.2)
(2.2)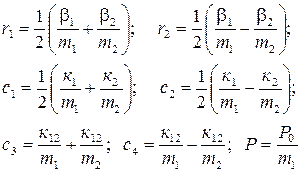
 (2.3)
(2.3)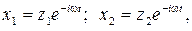
 .
.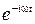 , получим
, получим (2.4)
(2.4) (2.5)
(2.5)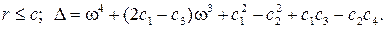
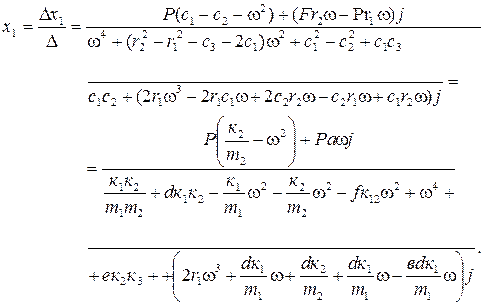 (2.6)
(2.6)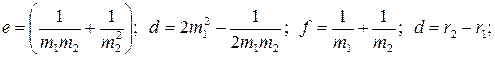
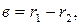
 и
и 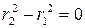 .
.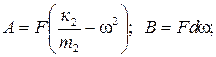
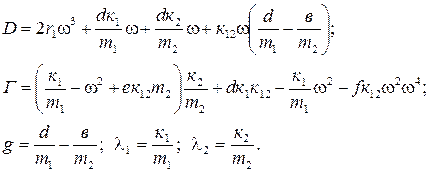
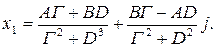
 ,
, .
. (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) . (2.10)
. (2.10)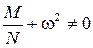 ,
,
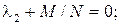 откуда
откуда 
 . Подставив полученные корни в решение (2.8)
. Подставив полученные корни в решение (2.8) . (2.11)
. (2.11)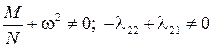
 . Определение коэффициента связи (жесткости резания) было найдено аналитически. Это дает основание в принятой модели процесс резания представить в виде пружины с коэффициентом жесткости к 12 = кв, где
. Определение коэффициента связи (жесткости резания) было найдено аналитически. Это дает основание в принятой модели процесс резания представить в виде пружины с коэффициентом жесткости к 12 = кв, где  - удельная сила резания (отнесенная к площади срезаемого слоя), z - усадка стружки, для сталей среднее значение z0 = 3, s = (1,3 … 1,4)s в, где s в = 4,8 … 8,0 Н/мм2, в - ширина срезаемого слоя. Численное решение (2.9) представлено сплошными линиями на графиках рис. 2.3. Из рассмотрения результатов видно, что в отсутствие демпфирования в системе можно полностью устранить АОК в широком диапазоне частот (скорости вращения шпинделя), прочностных характеристик s0 материала заготовки, ширины срезаемого слоя и усадки стружки z.
- удельная сила резания (отнесенная к площади срезаемого слоя), z - усадка стружки, для сталей среднее значение z0 = 3, s = (1,3 … 1,4)s в, где s в = 4,8 … 8,0 Н/мм2, в - ширина срезаемого слоя. Численное решение (2.9) представлено сплошными линиями на графиках рис. 2.3. Из рассмотрения результатов видно, что в отсутствие демпфирования в системе можно полностью устранить АОК в широком диапазоне частот (скорости вращения шпинделя), прочностных характеристик s0 материала заготовки, ширины срезаемого слоя и усадки стружки z.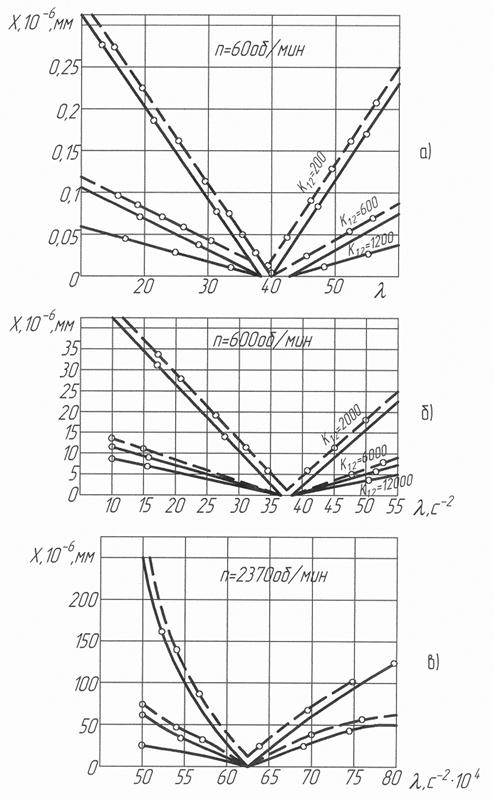
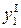 - первую составляющую, которая пропорциональна Р и силе резания. Воздействие резцовой группы на деталь порождает вторую составляющую -
- первую составляющую, которая пропорциональна Р и силе резания. Воздействие резцовой группы на деталь порождает вторую составляющую - 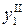 движения заготовки. В итоге после суммирования
движения заготовки. В итоге после суммирования  .
.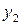 . Последнее, алгебраически суммируясь с
. Последнее, алгебраически суммируясь с 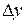 .
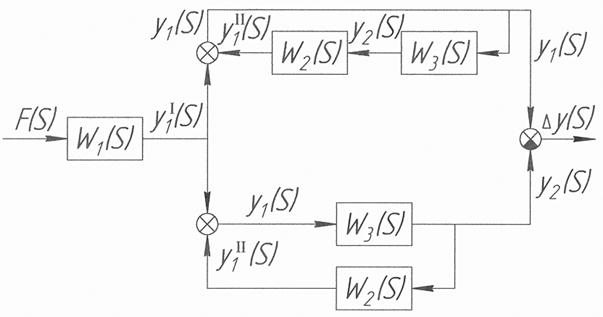
.
 (2.12)
(2.12)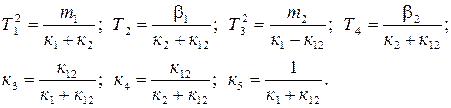
 (2.13)
(2.13) ;
;  ;
;  имеют вид:
имеют вид: (2.14)
(2.14) (2.15)
(2.15) . (2.16)
. (2.16) входит коэффициент жесткости резания к 12, через который осуществляется не показанная на структуре связь между ПДО и ПРС. Кроме того, в каждую из ветвей структуры входят передаточные функции (рис.2.4), содержащие параметры, присущие указанным подсистемам. Соответственно имеет место их взаимовлияние при формировании
входит коэффициент жесткости резания к 12, через который осуществляется не показанная на структуре связь между ПДО и ПРС. Кроме того, в каждую из ветвей структуры входят передаточные функции (рис.2.4), содержащие параметры, присущие указанным подсистемам. Соответственно имеет место их взаимовлияние при формировании 



 . Их анализ показывает, что с увеличением коэффициента связи к 12 амплитуда
. Их анализ показывает, что с увеличением коэффициента связи к 12 амплитуда  (рис.2.5, б) приводят к следующим выводам:
(рис.2.5, б) приводят к следующим выводам:  , как видно здесь влияние к 12 аналогично предыдущему случаю.
, как видно здесь влияние к 12 аналогично предыдущему случаю.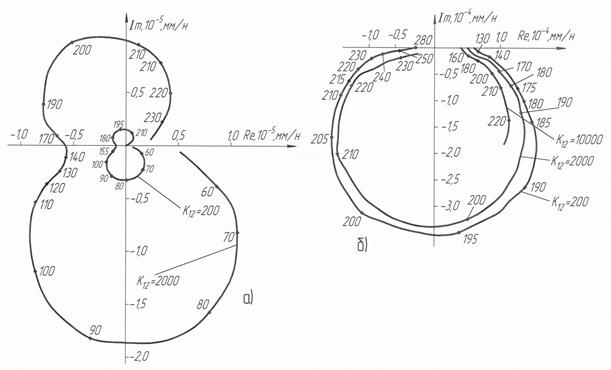
 ), уточним математическое описание объекта. Тогда уравнения (2.1), описывающие объект управления как двухмассовую модель, примут вид:
), уточним математическое описание объекта. Тогда уравнения (2.1), описывающие объект управления как двухмассовую модель, примут вид: (2.17)
(2.17) (2.18)
(2.18) ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 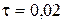
 (2.19)
(2.19)
 и
и  ), а в другой - три (
), а в другой - три (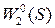 …
… 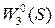 ). Причем, между
). Причем, между  . На выходам этих ветвей -
. На выходам этих ветвей -  (2.20)
(2.20) . (2.21)
. (2.21)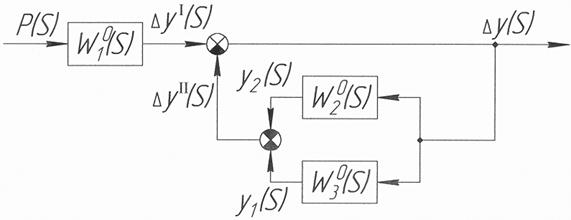
 …
… 
 (по критерию устойчивости Настквиста), охватывающей точку - 1, j, 0 показывает, что система неустойчива. Такое расположение годографа АФЧХопределяется значениями коэффициента к 12 и времени t, т.е. режимом резания, геометрией инструмента, прочностными свойствами обрабатываемого материала, технологическим состоянием самого станка и т.д.
(по критерию устойчивости Настквиста), охватывающей точку - 1, j, 0 показывает, что система неустойчива. Такое расположение годографа АФЧХопределяется значениями коэффициента к 12 и времени t, т.е. режимом резания, геометрией инструмента, прочностными свойствами обрабатываемого материала, технологическим состоянием самого станка и т.д.