Производная по заданному направлению. Градиент
Из определения частных производных и из механического смысла 1-й производной следует, что 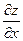 и и 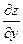 характеризуют скорость изменения функции характеризуют скорость изменения функции  в положительном направлении осей Ох и Оу соответственно. Но в ряде приложений математического анализа приходится рассматривать вопрос о быстроте изменения функции в положительном направлении осей Ох и Оу соответственно. Но в ряде приложений математического анализа приходится рассматривать вопрос о быстроте изменения функции 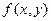 при смещении точки при смещении точки 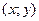 в произвольном направлении. Решение этого вопроса приводит к понятию производной функции по заданному направлению. в произвольном направлении. Решение этого вопроса приводит к понятию производной функции по заданному направлению.
Пусть в некоторой области D задана функция двух переменных  . Возьмем в D точку . Возьмем в D точку 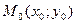 и проведем через нее прямую l. Придадим ей определенное направление. Пусть и проведем через нее прямую l. Придадим ей определенное направление. Пусть 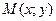 – точка прямой l, лежащая в D и такая, что отрезок – точка прямой l, лежащая в D и такая, что отрезок 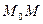 принадлежит D. Разность принадлежит D. Разность 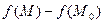 назовем приращением функции назовем приращением функции 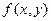 по данному направлению l и обозначим ее через по данному направлению l и обозначим ее через 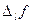 , т.е. , т.е. 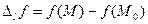 . Составим . Составим
| |         
отношение 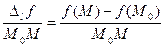 , взяв длину отрезка , взяв длину отрезка 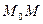 со знаком плюс, если направление этого отрезка совпадает с прямой l, и со знаком минус в противном случае. Это отношение называют средней скоростью изменения функции со знаком плюс, если направление этого отрезка совпадает с прямой l, и со знаком минус в противном случае. Это отношение называют средней скоростью изменения функции  при переходе из точки при переходе из точки 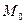 в точку М по направлению l. в точку М по направлению l.
Если существует
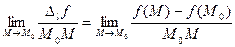 , ,
то он называется производной в точке 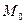 от функции от функции 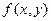 по направлению l и обозначается по направлению l и обозначается 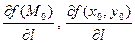 или или 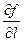 . .
Эту производную естественно рассматривать как скорость изменения функции 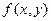 в данной точке в данной точке 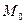 по направлению прямой l. При этом по направлению прямой l. При этом 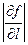 определяет величину скорости, а знак производной – возрастание (при определяет величину скорости, а знак производной – возрастание (при  и убывание (при и убывание (при 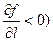 функции функции 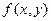 в направлении l. в направлении l.
Если прямая l совпадает с Ох или Оу, то получаем частные производные 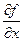 и и 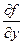 соответственно, т.е. производная по направлению является обобщением частных производных. соответственно, т.е. производная по направлению является обобщением частных производных.
Установим достаточные условия существования производной по направлению и формулу для ее вычисления.
Теорема. Если функция 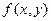 дифференцируема в точке дифференцируема в точке 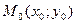 области D, то она имеет в этой точке производную по любому направлению l, причем области D, то она имеет в этой точке производную по любому направлению l, причем
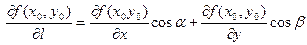 , (22.1) , (22.1)
где 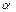 и и 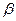 – углы, образованные направлением прямой l соответственно с положительными направлениями осей Ох и Оу. – углы, образованные направлением прямой l соответственно с положительными направлениями осей Ох и Оу.
Доказательство. В силу дифференцируемости функции 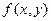 в точке в точке 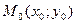 приращение приращение 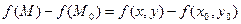 можно записать в виде можно записать в виде
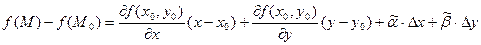 , ,
где 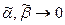 при при 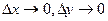 . Отсюда . Отсюда
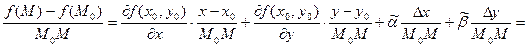
|см. рисунок| 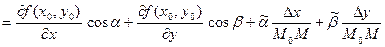 . .
Поскольку 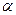 и и 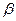 постоянны, а постоянны, а 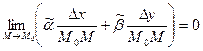 (так как (так как 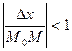 и и 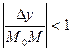 ), имеем ), имеем
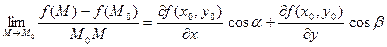 , ,
т.е. производная 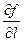 существует и существует и
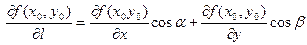 . .
Теорема доказана.
В случае функции большего числа переменных производная по направлению определяется и вычисляется аналогично. Например, для функции 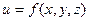
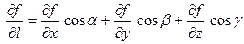 , ,
где 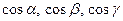 – направляющие косинусы прямой l. – направляющие косинусы прямой l.
Для изучения вопроса о направлении быстрейшего возрастания функции  введем в рассмотрение вектор с координатами введем в рассмотрение вектор с координатами 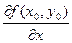 и и 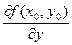 . Этот вектор называется градиентом функции . Этот вектор называется градиентом функции 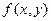 в точке в точке 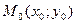 и обозначается и обозначается  , а в произвольной точке , а в произвольной точке 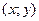 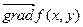 или или 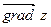 . Таким образом, . Таким образом,
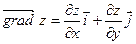 , ,
где производные 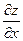 и и 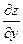 вычислены в соответствующей точке. вычислены в соответствующей точке.
Предположим, что функция  дифференцируема в некоторой области. Тогда в любой точке дифференцируема в некоторой области. Тогда в любой точке 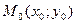 этой области существует производная этой области существует производная 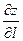 по любому направлению l, определяемая по формуле (22.1). Выразим эту производную через градиент данной функции. Рассмотрим единичный вектор по любому направлению l, определяемая по формуле (22.1). Выразим эту производную через градиент данной функции. Рассмотрим единичный вектор 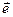 , имеющий то же направление, что и прямая l. Ясно, что проекции , имеющий то же направление, что и прямая l. Ясно, что проекции 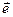 на Ох и Оу равны на Ох и Оу равны 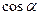 и и 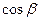 , т.е. , т.е.     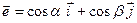 . Тогда очевидно, что . Тогда очевидно, что 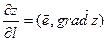 – скалярное произведение, или – скалярное произведение, или 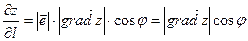 , так как , так как 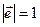 , где , где 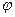 – угол между векторами – угол между векторами 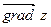 и и 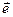 . Таким образом, производная по направлению равна проекции градиента на это . Таким образом, производная по направлению равна проекции градиента на это
| |
направление.
Из последней формулы видим, что производная по направлению 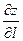 в точке в точке 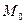 имеет наибольшее значение, и притом положительное, при имеет наибольшее значение, и притом положительное, при 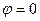 , т.е. когда производная функции в точке , т.е. когда производная функции в точке 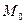 берется по направлению, определяемому градиентом этой функции в точке берется по направлению, определяемому градиентом этой функции в точке 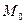 . При этом . При этом
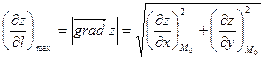 . .
Таким образом, модуль градиента дифференцируемой функции равен наибольшему значению 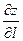 , т.е. наибольшей скорости изменения функции z в данной точке, а направление градиента данной функции в рассматриваемой точке совпадает с тем, для которого это наибольшее значение , т.е. наибольшей скорости изменения функции z в данной точке, а направление градиента данной функции в рассматриваемой точке совпадает с тем, для которого это наибольшее значение  достигается. Ясно, что направление, противоположное градиенту, является направлением наиболее быстрого убывания функции. достигается. Ясно, что направление, противоположное градиенту, является направлением наиболее быстрого убывания функции.
Пример 1. Найдем производную функции 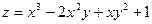 в точке М(1;2) в направлении, идущем от этой точки к точке N (4;6). в точке М(1;2) в направлении, идущем от этой точки к точке N (4;6).
Решение. Имеем  , т.е. , т.е. 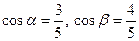 , частные производные функции , частные производные функции 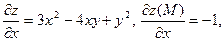 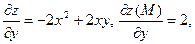 поэтому поэтому 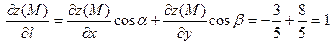 . .
Ответ: 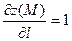 . .
Пример 2. Найдем 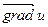 в точке М (1;2;3), если в точке М (1;2;3), если 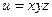 . .
Решение. Имеем 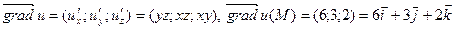 . .
Дата добавления: 2015-01-18 | Просмотры: 1352 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|






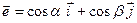 . Тогда очевидно, что
. Тогда очевидно, что 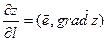 – скалярное произведение, или
– скалярное произведение, или 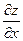 и
и 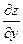 характеризуют скорость изменения функции
характеризуют скорость изменения функции  в положительном направлении осей Ох и Оу соответственно. Но в ряде приложений математического анализа приходится рассматривать вопрос о быстроте изменения функции
в положительном направлении осей Ох и Оу соответственно. Но в ряде приложений математического анализа приходится рассматривать вопрос о быстроте изменения функции 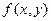 при смещении точки
при смещении точки 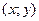 в произвольном направлении. Решение этого вопроса приводит к понятию производной функции по заданному направлению.
в произвольном направлении. Решение этого вопроса приводит к понятию производной функции по заданному направлению.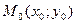 и проведем через нее прямую l. Придадим ей определенное направление. Пусть
и проведем через нее прямую l. Придадим ей определенное направление. Пусть 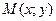 – точка прямой l, лежащая в D и такая, что отрезок
– точка прямой l, лежащая в D и такая, что отрезок 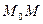 принадлежит D. Разность
принадлежит D. Разность 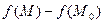 назовем приращением функции
назовем приращением функции 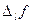 , т.е.
, т.е. 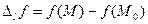 . Составим
. Составим
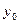
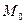
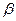
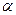 О
О 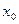
 х х
х х
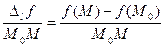 , взяв длину отрезка
, взяв длину отрезка 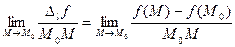 ,
,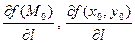 или
или 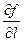 .
.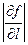 определяет величину скорости, а знак производной – возрастание (при
определяет величину скорости, а знак производной – возрастание (при  и убывание (при
и убывание (при 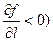 функции
функции 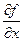 и
и 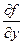 соответственно, т.е. производная по направлению является обобщением частных производных.
соответственно, т.е. производная по направлению является обобщением частных производных.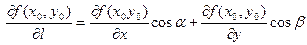 , (22.1)
, (22.1)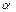 и
и 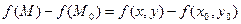 можно записать в виде
можно записать в виде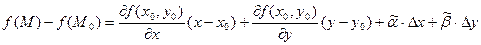 ,
,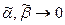 при
при 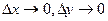 . Отсюда
. Отсюда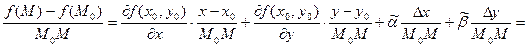
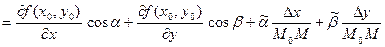 .
.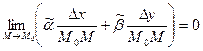 (так как
(так как 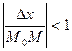 и
и 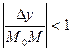 ), имеем
), имеем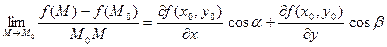 ,
,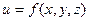
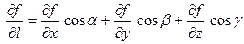 ,
,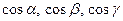 – направляющие косинусы прямой l.
– направляющие косинусы прямой l.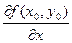 и
и 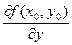 . Этот вектор называется градиентом функции
. Этот вектор называется градиентом функции  , а в произвольной точке
, а в произвольной точке 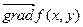 или
или 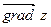 . Таким образом,
. Таким образом,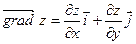 ,
,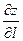 по любому направлению l, определяемая по формуле (22.1). Выразим эту производную через градиент данной функции. Рассмотрим единичный вектор
по любому направлению l, определяемая по формуле (22.1). Выразим эту производную через градиент данной функции. Рассмотрим единичный вектор 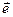 , имеющий то же направление, что и прямая l. Ясно, что проекции
, имеющий то же направление, что и прямая l. Ясно, что проекции 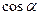 и
и 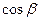 , т.е.
, т.е. 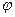
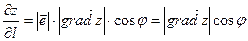 , так как
, так как 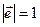 , где
, где 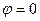 , т.е. когда производная функции в точке
, т.е. когда производная функции в точке 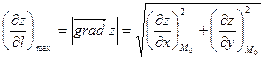 .
.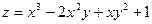 в точке М(1;2) в направлении, идущем от этой точки к точке N (4;6).
в точке М(1;2) в направлении, идущем от этой точки к точке N (4;6). , т.е.
, т.е. 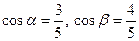 , частные производные функции
, частные производные функции 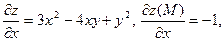
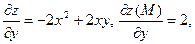 поэтому
поэтому 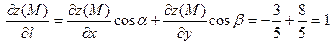 .
.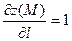 .
.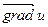 в точке М (1;2;3), если
в точке М (1;2;3), если 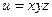 .
.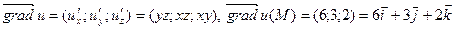 .
.