 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Понятие, предел и непрерывность функции нескольких переменных 7 страница
Выполним расчет вероятности безопасного прохода судна по выходу из порта Ливерпуль.
где: где: dМС – средняя квадратическая погрешность места судна; МСМ – средняя квадратическая погрешность счислимого места судна.
где: М 0 – последняя обсервация с помощью РЛС. КС – коэффициент счисления, принимаем равным 0,2; t – время до траверза опасности, t = 0,5. Обсервацию проводим по 2-м дистанциям по формуле:
Находим нормированное по средней квадратической величине mD расстояние до опасности по нормали к линии пути по формуле:
Оценку надёжности прохождения судна мимо опасности рассчитываем по формуле:
Для случая односторонней опасности показатель надежности Р благополучного прохода рассчитываем по формуле:
где: РОП – вероятность отсутствия необнаруженных промахов, РОП = 0,95.
Полученные результаты сводим в таблицу 2.20.
Таблица 2.20 – Расчет оценки навигационной безопасности
В целом же, вопрос о том какой уровень навигационной безопасности считать разумно достаточным зависит от многих дополнительных аргументов и решается конкретно для каждого отдельного случая. 2.4. Учет маневренности судна.
В стесненных водах, где через навигационные опасности и интенсивное судоходство ограниченный выбор маневра, суда проводят 5-10% ходового времени. Но именно здесь происходит более 80% всех навигационных аварий. Главной особенностью судовождения в таких водах есть то, что путь судна определен навигационной обстановкой: -плавания происходит в непосредственной близости от навигационных опасностей; -ширина фарватера находится в предельном соотношении с шириной полосы, которая очерчивается судном; -изменяется направление фарватера; -наблюдаются резкие перепады глубин, а также значительного приливного колебания уровня моря и приливные течения; -плавания происходит при сниженных скоростях, когда силы внешних влияний на судно в сравнении с силами управляющих влияний, т.е. движение происходит на гране потери управляемости. Навигационная подготовка к плаванию в стесненных водах включает: -тщательное предыдущее планирование пути судна; -более частое определение места судна; -повышенную точность исчисления пути судна; -контроль за достоверностью узнавания ориентиров; -учет ветрового дрейфа и износа от течения. При плавании в сжатых водах необходимо учитывать ширину полосы Вп, занятой судном при дрейфе и течении и зависимой от длины L и ширины В судна. Ширину полосы определяют по формуле:
где: С° = 3° - суммарный угол износа, который учитывается, от дрейфа, течения, рыскание при управлении судном и погрешностей их определения.
Ширина полосы Вп при повороте больше на величину ∆В, что по обобщенным статистическим данным оценивается по формуле:
Т.к. длина судна L = 134б55 м, тогда:
В=Вп+∆В (2.20)
Тогда получим:
В = 23,5 + 47,1 = 70,6 м.
Опасные участки в стесненных водах необходимо определять раньше времени. Следует принимать все предупредительные меры как при планировании перехода, так и во время плавания. К таким мерам относятся: выбор времени прохождения опасных участков в зависимости от естественной освещенности, прогнозов погоды, заведомо рассчитанных уровней воды в приливных районах.
2.5. Подъем карт.
Подъём карт выполняют с учётом особенностей судна, намечаемого пути и времени перехода. Это повышает их информативность и облегчает решение задач в плавание. Процедура нанесения на карты дополнительной навигационной информации, особо выделяя на них те сведения, которые будут иметь важное значение при выполнении намеченного перехода носит название «подъём карт» и осуществляется обычными цветными карандашами, а в отдельных случаях и цветной тушью. Подъем карт - особая процедура, заключающаяся в нанесении на карты дополнительной навигационной информации. Осуществляется подъем карт обычным и цветным карандашом. Прежде всего, необходимо нанести на карты границы районов действия особых правил плавания. Наиболее важные сведения из таких правил можно выписать на нерабочем месте карты. Цветным карандашом отмечают участки берега и ориентиры, четко отображаемые на экранах НРЛС. Далее простым карандашом наносят границы дальности видимости маяков и знаков, магнитное склонение приводится к году плавания. Особое внимание уделяется подъему карт на тех участках, где путь судна пролегает в непосредственной близости от различного рода опасностей, а так же там, где он проходит через узости и акватории, стесненные навигационными опасностями. В таких случаях более четко выделяют секторы маяков, ограждающие опасности. В целях обеспечения судовождения на случай пониженной видимости необходимо наметить и провести предостерегающие изобаты, цветным карандашом отметить границы акватории, выделить районы с характерным рельефом дна, пригодные для определения места судна по глубинам, провести ограждающие изобаты. Опасный для навигации участок показан на рисунке 2.4 и на плакате.
Рисунок 2.4 – Опасный участок
2.6 Составление маршрутных листов.
В соответствии с рекомендациями ИМО, навигационная подготовка к переходу должна заканчиваться составлением маршрутных листов, которые должны лежать на штурманском столе. Безусловно, в течение рейса в маршрутные листы вносятся необходимые изменения. Имеются три формы маршрутных листов: для океанского участка, для прибрежного и для участка лоцманской проводки. Пример маршрутного листа с реального рейса приведен в приложении.
2.7 Графический план перехода.
Результаты всей предыдущей работы по навигационному проектированию перехода оформляют в виде графического плана перехода. По координатам поворотных точек на план наносят намеченный путь судна и у каждого участка надписывают путевой угол и плавания по нему. Поперечными засечками намечают на линии пути места восхода и заката Солнца и Луны, надписывая расчетное судовое время явления. На крупномасштабном плане опасного участка дополнительно отмечают пеленги ожидаемого открытия и закрытие маяков. На плане для каждого участка перехода надписывают основные и резервные способы намеченных обсерваций с указанием ориентиров. На крупномасштабном плане опасного участка отмечают красным все навигационные опасности. При возможности на план перехода наносят ожидаемую гидрометеорологическую обстановку и все другие сведения которые влияют или могут повлиять на безопасность плавания. Графический план перехода представлен на плакате и на рисунке 2.5. .
Понятие, предел и непрерывность функции нескольких переменных
Понятие функции нескольких переменных вводится с помощью понятия отображения множеств, которое было нами введено в 1 семестре. Определение 1. Пусть Х – множество пар (х; у) действительных чисел. Отображение f Х в R, сопоставляющее каждой паре чисел (х; у) Аналогично определяется функция трех переменных Определение 2. Естественной областью определения функции нескольких переменных называется множество значений ее аргументов, при которых функция имеет смысл. Пример 1. Найдем области определения функций Решение. Все три функции имеют смысл, когда подкоренные выражения неотрицательны, т.е. Для функции
  О х x О х x
y y При Как известно, каждой точке плоскости с заданной декартовой системой координат соответствует единственная пара чисел – ее координат, и наоборот. Поэтому пары чисел и точки плоскости можно отождествлять и для пар чисел применять геометрическую терминологию, называя пару чисел (х; у) точкой плоскости. Аналогично, тройку чисел Продолжая аналогию, назовем n -мерной точкой систему n действительных чисел:
n -мерное пространство с введенным по формуле (18.1) расстоянием между любыми его двумя точками называется n-мерным евклидовым пространством В качестве окрестности точки
Определение 3. Предельной точкой данного множества Е точек пространства Как и в случае множества одномерного пространства, т.е. множества числовой прямой, предельная точка Определение 4. Непустое n -мерное точечное множество называется замкнутым, если оно содержит все свои предельные точки. Таким образом, множество Определение 5. Точка А данного n -мерного множества Е называется его внутренней точкой, если существует такая окрестность этой точки, которая целиком состоит из точек данного множества. n -мерное точечное множество называется открытым, если все его точки являются внутренними. Например, круг Определение 6. Пусть
Пишут: Можно дать и другое определение предела функции в точке (на языке последовательностей), равносильное данному определению. Определение 7. Пусть Второе определение особенно полезно при доказательстве того, что функция не имеет предела в данной точке. Для этого достаточно указать две последовательности точек, сходящихся к данной точке, такие, что соответствующие последовательности значений функции сходятся к разным пределам. Часто оказывается удобным брать последовательности точек на кривых, проходящих через предельную точку, причем при движении по кривой координаты могут изменяться и непрерывно. Пример 2. Покажем, что функция Решение. Заметим, что через начало координат
Видим, что величина предела зависит от k, т.е. от пути движения к предельной точке. Поэтому предела нет. Бесконечно малые и бесконечно большие функции, предел функции на бесконечности определяются аналогично случаю функции одной переменной. При вычислении пределов функции нескольких переменных можно использовать замечательные пределы. Пример 3. На пределы функций нескольких переменных распространяются основные теоремы о пределах, доказанные нами для функций одной переменной: об ограниченности функции, имеющей предел, о пределе суммы, произведения и частного функций, леммы о бесконечно малых функциях и т.д. Доказательства их аналогичны приведенным в 1-м семестре. Введем теперь понятие непрерывности функции нескольких переменных. Определение 8. Функция короче, Пример 4. Покажем, что функция Решение. Для любой точки Для того, чтобы доказать непрерывность функции в точке
Пример 5. Исследуем на непрерывность функцию Решение. Так же, как в примере 4, с помощью теорем о пределе функции доказываем непрерывность функции Таким образом, функция Пример 6. Исследуем на непрерывность функцию Решение. Так же, как в примерах 4 и 5, доказывается, что функция Для функций нескольких переменных имеет место ряд теорем, аналогичных соответствующим теоремам для функций одной переменной: теоремы о непрерывности суммы, произведения, частного непрерывных функций, сложной функции и т.д. Справедливы также теоремы, аналогичные теоремам Вейерштрасса и Больцано-Коши.
Дата добавления: 2015-01-18 | Просмотры: 1127 | Нарушение авторских прав |
 (2.12)
(2.12)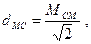
 (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18)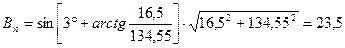 м
м (2.19)
(2.19) м
м
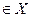 число
число  , называется функцией двух переменных, заданной на множестве Х. При этом х и у называются аргументами функции f, Х – областью ее определения,
, называется функцией двух переменных, заданной на множестве Х. При этом х и у называются аргументами функции f, Х – областью ее определения,  – значением функции. Множество
– значением функции. Множество 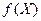 называется множеством значений функции.
называется множеством значений функции.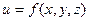 и функция n переменных
и функция n переменных 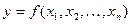 , если в качестве Х рассматривать множества систем
, если в качестве Х рассматривать множества систем  и
и  действительных чисел соответственно.
действительных чисел соответственно. ,
, 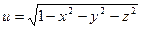 ,
,  .
. . В первом случае имеем
. В первом случае имеем  – круг с центром в начале координат и радиусом 1, во втором –
– круг с центром в начале координат и радиусом 1, во втором –  – шар с центром в начале координат и радиусом 1, в третьем случае
– шар с центром в начале координат и радиусом 1, в третьем случае  – n -мерный шар с центром в начале координат и радиусом 1.
– n -мерный шар с центром в начале координат и радиусом 1.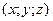 трехмерного пространства, для которых
трехмерного пространства, для которых  , а z – значение функции в точке (х; у). Графиком обычно является некоторая поверхность. Например, графиком функции
, а z – значение функции в точке (х; у). Графиком обычно является некоторая поверхность. Например, графиком функции  является поверхность параболоида вращения, график функции
является поверхность параболоида вращения, график функции 



 z
z
 z
z
 график функции
график функции  , а числа
, а числа  назовем координатами точки М. Множество всех n -мерных точек назовем n-мерным пространством. Обобщая известную формулудля расстояния между двумя точками плоскости, определим расстояние между точками
назовем координатами точки М. Множество всех n -мерных точек назовем n-мерным пространством. Обобщая известную формулудля расстояния между двумя точками плоскости, определим расстояние между точками  n -мерного пространства формулой
n -мерного пространства формулой . (18.1)
. (18.1) . При
. При  получаем евклидову плоскость, при
получаем евклидову плоскость, при  – трехмерное евклидово пространство.
– трехмерное евклидово пространство. n -мерного евклидова пространства будем рассматривать n -мерный шар с центром в этой точке, т.е. множество всех точек
n -мерного евклидова пространства будем рассматривать n -мерный шар с центром в этой точке, т.е. множество всех точек  . (18.2)
. (18.2)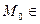
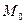 точка М этого множества.
точка М этого множества. , где m и n – любые натуральные числа, точка
, где m и n – любые натуральные числа, точка  – предельная, не принадлежащая этому множеству. Если же множество Е =
– предельная, не принадлежащая этому множеству. Если же множество Е =  (прямоугольник), то все его предельные точки принадлежат этому множеству.
(прямоугольник), то все его предельные точки принадлежат этому множеству.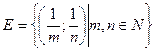 не является замкнутым, а прямоугольник Е =
не является замкнутым, а прямоугольник Е =  – открытое множество, открытым множеством является и все пространство
– открытое множество, открытым множеством является и все пространство  – предельная точка области определения
– предельная точка области определения  функции
функции  n переменных. Число l называется пределом этой функции в точке А, если для любого
n переменных. Число l называется пределом этой функции в точке А, если для любого  найдется окрестность точки А такая, что для всех точек
найдется окрестность точки А такая, что для всех точек  этой окрестности,
этой окрестности,  , имеет место неравенство
, имеет место неравенство , т.е.
, т.е. 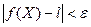 .
. или
или  .
. , принадлежащих
, принадлежащих  сходится к числу l.
сходится к числу l. в точке
в точке  не имеет предела.
не имеет предела. , где k = const. Найдем предел функции, когда точка
, где k = const. Найдем предел функции, когда точка 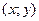 приближается к точке О по прямой
приближается к точке О по прямой 
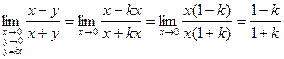 .
. при
при  и
и  .
.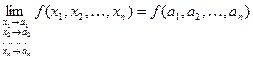 , или,
, или,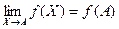 . В противном случае функция терпит разрыв в точке А, А – точка разрыва функции.
. В противном случае функция терпит разрыв в точке А, А – точка разрыва функции. непрерывна в каждой точке
непрерывна в каждой точке  .
.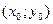 , отличной от точки
, отличной от точки 
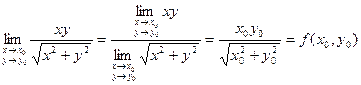 , т.е. в этой точке функция непрерывна.
, т.е. в этой точке функция непрерывна.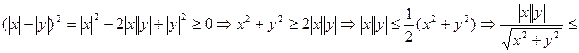
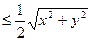 . Поскольку
. Поскольку  , то и
, то и 
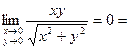 =
= 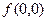 по теореме о промежуточной переменной, т.е. требуемое равенство выполнено.
по теореме о промежуточной переменной, т.е. требуемое равенство выполнено.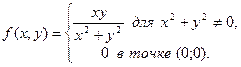
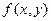 в точке
в точке  – зависит от k, т.е. предел не существует, поэтому функция разрывна в этой точке.
– зависит от k, т.е. предел не существует, поэтому функция разрывна в этой точке. и терпит разрыв в точке
и терпит разрыв в точке  .
. . Если
. Если  , то функция терпит разрыв, так как в этих точках функция не определена, т.е. функция разрывна в точках прямой
, то функция терпит разрыв, так как в этих точках функция не определена, т.е. функция разрывна в точках прямой