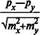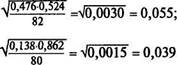АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

СОВОКУПНОСТЕЙ

При сравнении средних арифметических двух генеральных со­вокупностей любая разность между ними будет достоверна. В ве­теринарии, зоотехнии и т. д. приходится сравнивать между собой средние величины не генеральных совокупностей, а выборочных (породы, линии, семейства, опытная и контрольная группы и т. д.). Поэтому необходимо установить достоверность разности между средними двух групп. Недостаточно, например, знать, что 20 дочерей какого-то производителя превосходят по удою своих матерей. Следует, кроме того, вычислить критерий достоверности разности, чтобы с определенной вероятностью судить о том, что следующие 100, 200 и т. д. дочерей этого производителя также будут превосходить по молочности своих матерей в аналогичных условиях. Для оценки достоверности разности между средними арифметическими двух выборочных совокупностей применяется критерий достоверности (td), который вычисляют по формуле

где mi, тг — ошибки сравниваемых выборочных средних арифметических х\, xj; d —разность между средними арифметическими х\, хг; пи —средняя ошибка выборочной разности; /«— стандартное значение критерия, определяемое по таб­лице Стьюдента (табл. 13) с учетом числа степеней свободы (v) для трех уровней вероятности; щ, т — численность сравниваемых групп.

Пример. Нужно установить, различаются ли дочери двух быков по титру лизоцима в крови, если получены следующие показатели:

_т =

= 0,005, или 0,5 %.

30; xi±»»i = l,612±0,021g5 28; х_г±т₂= l,538±0,031gx

Для этого определяем

_t _ 1,612—1,538 _ 0,074 _ 0,074 _ 2 06
V^{2 2} ~^Щ~°^О36~ '

По таблице 13 с учетом числа степеней свободы v = Л1 + яг — 2 = 30 + 28 — 2 = 56 находим значения fa (нижняя строка), которые равны: при р = 0,95 У = 1,96; при р = 0,99 fe = 2,58 и при р = 0,999 U = 3,29. Сравниваем величину U с t_st. Здесь возможны два вывода: 1) если и равен или больше значения t_s, для первого уровня вероятности {td £ fe), то раз­ность между средними арифметическими двух групп статистически достоверна; 2) если td меньше значения tst для первого уровня вероятности, то разность между средними арифметическими двух групп статистически недостоверна. В нашем примере td = 2,06 больше значения /_я = 1,96 для первого уровня вероятности (0,95), н». меньше fe = 2,58 для второго уровня вероятности (0,99). Поэтому нужно сделать следующий вывод: разность между потомством двух производите­лей по титру лизоцима в крови достоверна с вероятностью р > 0,95. У дочерей первого быка более высокий титр лизоцима в крови.

Статистический анализ изменчивости по качественным призна­кам. Средняя арифметическая для качественных признаков отра­жает долю или процент особей, имеющих данный признак. На­пример, в одном хозяйстве из 1030 коров заболело лейкозом 28 голов и 1002 остались здоровыми. В этом случае совокупность состоит из двух групп: первая — больные животные, вторая — здоровые. Численность первой группы обозначим р\, числен­ность второй — ро, общую численность — п. Тогда долю больных (т. е. имеющих изучаемый признак) животных (р) определяют по формуле

^ ^ = 0,027, или 2,7%.

Здесь р соответствует средней арифметической (х) при коли­чественной изменчивости. Доля здоровых животных (q) состав­ляет

Среднее квадратическое отклонение вычисляют по формуле c = <p~q~ = V0,027 0,973 = 0,163, или 16,3 %.

Средняя ошибка. Частота качественного признака, вы­раженная в долях единицы или в процентах, также имеет свою ошибку:

Ошибка является одинаковой для доли больных и здоровых животных: р±т = 0,027 + 0,005; q + m = 0,973 + 0,005, или 2,7 ±0,5 и 97,3 ±0,5%.

Определение достоверности разности между выборочными до­лями или процентами. 6 одном стаде из 82 дочерей быка № 25588 заболели бруцеллезом 39, а из 80 дочерей быка № 1406— 11. Необходимо установить, различаются ли производители по вос­приимчивости дочерей к бруцеллезу. Для этого воспользуемся формулой

_t -

82 = 0,476 и

_т -

У

По таблице 13 с учетом числа степеней свободы v = п_х + + п_у — 2 = 82 + 80 — 2 = 160 находим значения у (последняя строка), которые равны 1,96; 2,58; 3,29. Так как величина td = 14,9 больше у ⁼ 3,29 для третьего уровня вероятности, можно сделать вывод: разность между быками-производителя­ми по частоте заболевания дочерей бруцеллезом достоверна с вероятностью р > 0,999. Это значит, что дочери быка № 25588 отличаются большей восприимчивостью к бруцеллезу, чем по­томство производителя № 1406.

Дата добавления: 2015-12-16 | Просмотры: 470 | Нарушение авторских прав