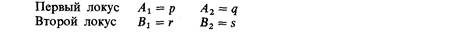АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 3. Пер. с англ.: – М.: Мир, 1988. – 336 с.

Прочитайте:
  1. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  2. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  3. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  4. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  5. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  6. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  7. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  8. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  9. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  10. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.

25. Инбридинг, коадаптация и дифференциация 181

дет повышаться, если аллели всегда (или чаще всего) будут передаваться из поколения в поколение в комбинациях А 1 В 1и А2В2 и никогда (или редко)-в комбинациях А1В2 или А2В1.

Когда аллели различных локусов в одних комбинациях встречаются чаще, чем в других, то говорят, что существует неравновесностъ по сцеплению. Когда же аллели различных локусов сочетаются друг с другом случайным образом (т. е. пропорционально частотам самих аллелей), то говорят, что популяция равновесна по сцеплению.

Предположим, что частоты аллелей двух локусов равны:

 

Значит, р + q= l и r + s=l. Если аллели двух локусов встречаются в популяции в случайных комбинациях, то теоретически ожидаемые частоты гамет четырех возможных типов задаются произведениями частот, входящих в эти гаметы аллелей, т.е.

Поскольку сочетания этих четырех типов исчерпывают все возможные комбинации аллелей, сумма их частот должна быть равна единице. Действительно,

рг + qs + ps + qr = p(r + s) + q(r + s) = p + q = 1.

Если сочетания аллелей в гаметах случайны, то произведение частот двух гамет, находящихся в состоянии «притяжения» (рг·qs = pqrs), равно произведению частот двух гамет, находящихся в состоянии «отталкивания» (ps · qr = pqrs). Однако если сочетания аллелей в гаметах неслучайны, то эти произведения различны. Их разность служит мерой неравновесности по сцеплению:

d — (частота А1В1) · (частота А2В2) — (частота A 1 B 2) · (частота А2B1)· Условие равновесия по сцеплению записывается, следовательно, как d = = 0.

 

Таблица 25.5. Максимально возможные значения неравновесности по сцеплению d для трех различных случаев. В первом столбце для каждого случая указана частота наиболее распространенного аллеля, одинаковая в обоих локусах
    Частота гамет
  Случай Α1Β1 А2В2 А 1 В2 А2В 1 d
1. Частота 0,5          
  Притяжение 0,5 0,5     (0,5 ·0,5) - (0·0) = 0,25
  Отталкивание     0,5 0,5 (0·0) -(0,5· 0,5)= -0,25
2. Частота 0,6          
  Притяжение 0,6 0,4     (0,6 ·0,4) -(0·0) = 0,24
  Отталкивание     0,6 0,4 (0·0) -(0,6· 0,4)= -0,24
3. Частота 0,9          
  Притяжение 0,9 0,1     (0,9 ·0,1) -(0·0) = 0,09
  Отталкивание     0,9 0,1 (0·0) -(0,9· 0,1)= -0,09

Дата добавления: 2015-12-16 | Просмотры: 376 | Нарушение авторских прав

При использовании материала ссылка на сайт medlec.org обязательна! (0.003 сек.)