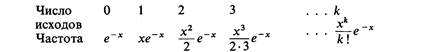АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 3. Пер. с англ.: – М.: Мир, 1988. – 336 с.

Прочитайте:
  1. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  2. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  3. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  4. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  5. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  6. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  7. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  8. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  9. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.
  10. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 2. Пер. с англ.: – М.: Мир, 1988. – 368 с.

Приложение 1. Вероятность и статистика 269

 

Таблица 6.П.1. Наблюдаемые и теоретически ожидаемые на основе распределения Пуассона результаты в эксперименте с бактериями
Число колоний на чашку Число чашек Число колоний Ожидаемая частота чашек Ожидаемое количество чашек
      0,311 18,7
      0,363 21,8
      0,212 12,7
      0,082 4,9
      0,024 1,44
    5 0,006 0,34
Всего     0,998 59,9

Когда вероятность отдельного события (в данном случае мутации) очень мала, а число испытаний (бактерий) очень велико, то частота событий подчиняется распределению Пуассона. (При этом предполагается также, что события независимы; в нашем примере это означает, что возникновение мутации у одной бактерии не влияет на вероятность ее возникновения у другой бактерии.) Другим примером пуассоновского распределения может служить число случаев ахондроплазии на каждые 10 000 новорожденных в браке нормальных родителей по всему населению земного шара.

Значения членов распределения Пуассона задаются следующей общей формулой:

 

где p (k) -вероятность того, что в данной выборке реализуется k интересующих нас исходов события, x -среднее число таких исходов в выборке данного размера, a k! (k факториал) - произведение вида 1·2·3... ·k. Другими словами, в соответствии с распределением Пуассона частоты выборок с данным числом исходов составляют:

В рассмотренном примере среднее число интересующих нас исходов (мутантов) в выборке (на чашке Петри) равно χ = 1,17. Ожидаемую частоту чашек Петри без колоний и с одной, двумя, тремя и т. д. колониями можно рассчитать по приведенной формуле членов распределения Пуассона (четвертый столбец таблицы П.6). Ожидаемое число чашек с соответствующим числом колоний (пятый столбец таблицы) получается умножением частоты на 60 - общее число чашек Петри в эксперименте. Теперь мы можем, например, определить с помощью критерия χ2, соответствуют ли результаты эксперимента теоретически ожидаемым на основе распределения Пуассона.

Удобная особенность пуассоновского распределения состоит в том, что у него среднее значение совпадает с дисперсией. Дисперсия данных,


Дата добавления: 2015-12-16 | Просмотры: 342 | Нарушение авторских прав

При использовании материала ссылка на сайт medlec.org обязательна! (0.003 сек.)