 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Виды распределений
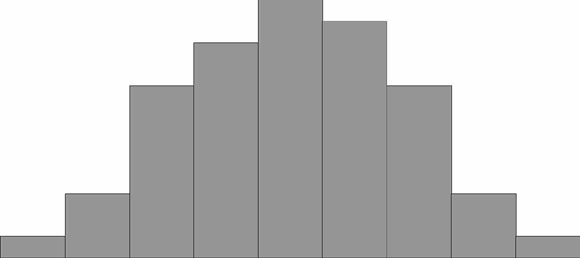
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход и т.п., а потом построить график любой из этих величин, то получится функция распределения данной величины. В зависимости от исследуемого признака получаемые графики могут быть различны. Посмотрим, как можно построить такой график на примере данных роста. Сначала, просто запишем результаты исследования. Потом, отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, "от 180 до 181 включительно". После этого необходимо посчитать количество людей в каждой подгруппе (диапазоне) – это будет частота попадания роста жителей города в данный диапазон. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить гистограмму – упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а высота будет равна той частоте, которая соответствует каждому диапазону роста. Если зарегистрированных данных было достаточно много, то полученный график будет выглядеть примерно так:
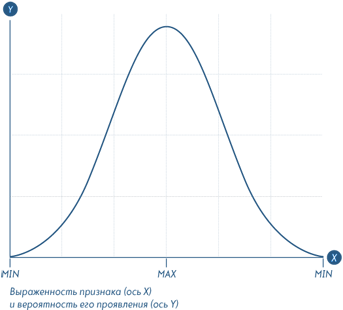
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения:
Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста – достоверное событие. Выделяют большое количество видов распределения признака в статистической совокупности. Остановимся на их краткой характеристике: 1) нормальное распределение 2) асимметричное распределение - правостороннее - левостороннее - бимодальное 3) альтернативное распределение
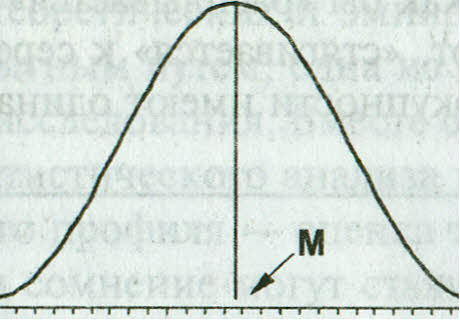
Нормальное (Гауссово, симметричное, колоколообразное) распределение – одно из самых важных распределений в статистике. Оно характеризуется тем, что наибольшее число наблюдений имеет значение, близкое к среднему, и чем больше значения отличаются от среднего, тем меньше таких наблюдений. Примерами характеристик, подчиняющихся нормальному распределению, являются показатели роста, веса, какие-либо биохимические показатели крови. Гауссово распределение характеризует распределение непрерывных случайных величин и встречается в природе наиболее часто, за что и получило название «нормального». Кривая нормального распределения имеет следующие свойства: · колоколообразна (унимодальна); · симметрична относительно среднего; · сдвигается вправо, если среднее увеличивается, и влево, если среднее уменьшается (при постоянной дисперсии). Среднее арифметическое, мода и медиана при нормальном распределении равны и соответствуют вершине распределения:
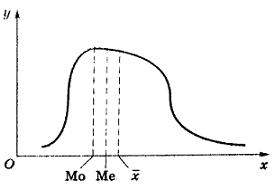
Нормальное распределение описывает явления, которые носят вероятностный, слу При асимметричном распределении данных наиболее полезной мерой центральной тенденции становится медиана. Это связано с тем, что на простую среднюю арифметическую сильно влияют экстремальные (очень высокие или очень низкие) значения, из-за чего она может стать причиной неверной интерпретации результатов. Медиана же менее подвержена влиянию экстремальных величин. Если график распределения имеет правостороннюю асимметрию ("хвост" вправо, в вариационном ряду преобладают варианты меньших значений), то в этом случае мода размещена левее, а среднее арифметическое (на рисунке обозначено как
Обратное расположение имеет место при левосторонней асимметрии графика. При этом, чем больше асимметричен график, тем больше расстояние между его средними точками. Проиллюстрируем важность выбора медианы, а не среднего арифметического значения на следующем примере. График заработной платы для жителей России имеет правостороннее асимметричное распределение (большинство людей имеет небольшую заработную плату). В силу того, что разброс минимальной и максимальной величин заработной платы очень велик, экстремальные значения сильно сказываются на значении среднего арифметического М (на рисунке обозначено как Бимодальное (двугорбое) распределение наблюдается тогда, когда исследуемый признак анализируется вне однородной совокупности и, следовательно, необходимо учитывать два средних значения признака для достоверного анализа. Пример: при оценке физического развития детей подростков распределение роста будет иметь две моды (соответствующие девочкам и мальчикам). Альтернативное распределение наблюдается в том случае, когда значения исследуемого признака распределяются по принципу: «да/нет», т.е. взаимоисключают друг друга. Подобное распределение характерно для описания качественных признаков (пример: мужской, женский пол).
Использование средних величин в медицине и здравоохранении: а) для оценки состояния здоровья — например, параметров физического развития (средний рост, средний вес, средний объем жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средний пульс, средняя СОЭ и др.); б) для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений за 1 ч. приема в поликлинике и др.); в) для оценки состояния окружающей среды.
В медицинских исследованиях из средних величин наиболее часто используется среднее арифметическое. В то же время, у больных людей значения многих физиологических параметров имеют асимметричное распределение, ввиду того, что изменяются в сторону увеличения или уменьшения под влиянием заболевания. Поэтому для характеристики центральной тенденции их распределения, во многих случаях, более обоснованным является как раз использование медианы, а не средней арифметической.
1. Вопросы по теме занятия:
1. Понятия генеральной и выборочной совокупностей. 2. Репрезентативность выборочной совокупности, качественная и количественная репрезентативность. 3. Одномерные, двумерные и многомерные наборы данных, понятия и примеры. 4. Виды признаков: качественные, порядковые, количественные. Их характеристика, примеры. 5. Факторные и результативные признаки. 6. Понятие временного ряда, медико-биологические примеры. 7. Шкалы измерения признаков. 8. Понятие вариационного ряда, его характеристики. 9. Виды вариационных рядов. 10. Понятия среднего арифметического, моды и медианы для вариационного ряда. Расчет этих характеристик. 11. Примеры использования среднего арифметического, моды и медианы в медицинских исследованиях. 12. Виды распределения случайной величины. 13. Мода, медиана и среднее арифметическое для нормального и ассиметричного распределений.
2. Тестовые задания по теме с эталонами ответов:
1. СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ – ЭТО 1) группа определенных признаков 2) группа объектов, обладающих признаками сходства и различия 3) группа относительно однородных элементов (единиц наблюдения), взятых в единых границах времени и пространства 4) группа явлений, объединенных в соответствии с целью исследования
2. ПЕРВИЧНЫМ ЭЛЕМЕНТОМ СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ ЯВЛЯЕТСЯ 1) объект наблюдения 2) признак 3) единица наблюдения 4) группа признаков
3. ЕДИНИЦА НАБЛЮДЕНИЯ В СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ – ЭТО 1) признак 2) первичный элемент совокупности, обладающий учитываемыми признаками 3) группа признаков 4) заболевание
4. ЕДИНИЦА СОВОКУПНОСТИ – ЭТО 1) описка по рассеянности или невнимательности 2) первичный элемент объекта статистического наблюдения, являющийся носителем признаков, подлежащих регистрации 3) разметка бланков по условным знакам 4) первичный элемент, из которых состоит вся наблюдаемая статистическая совокупность
5. ПРИЗНАК – ЭТО 1) объект статистического исследования 2) первичный элемент статистической совокупности 3) свойство, проявлением которого один предмет отличается от другого 4) характеристика статистической совокупности
6. К КАЧЕСТВЕННЫМ ПРИЗНАКАМ ОТНОСЯТСЯ 1) рост 2) пол 3) масса тела 4) жизненная емкость легких
7. К КОЛИЧЕСТВЕННЫМ ПРИЗНАКАМ ОТНОСЯТСЯ 1) рост 2) пол 3) исход заболевания 4) вид заболевания
8. ВЫБОРОЧНАЯ СОВОКУПНОСТЬ ЭТО 1) группа, состоящая из относительно однородных элементов, взятых в единых границах времени и пространства 2) совокупность, состоящая из всех единиц наблюдения, которые могут быть к ней отнесены в соответствии с целью исследования 3) часть генеральной совокупности, отобранная специальными методами и предназначенная для ее характерис-тики 4) совокупность всех единиц наблюдения, которые могут быть отнесены к ней в соответствии с целью исследования
9. РЕПРЕЗЕНТАТИВНОСТЬ – ЭТО 1) достаточный объем генеральной совокупности 2) достаточный объем выборочной совокупности 3) непохожесть выборочной совокупности на генеральную 4) способность выборочной совокупности наиболее полно представлять генеральную
10. РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНОЙ СОВОКУПНОСТИ ПО ОТНОШЕНИЮ К ГЕНЕРАЛЬНОЙ ОБЕСПЕЧИВАЕТ 1) обязательное соблюдение временных границ 2) достаточный объем наблюдений 3) оценка показателей в динамике 4) обязательное соблюдение пространственных границ
11. ДОСТОИНСТВА СРЕДНЕЙ ВЕЛИЧИНЫ СОСТОЯТ В ТОМ, ЧТО ОНА 1) позволяет анализировать большое число наблюдений 2) позволяет выявить закономерности при малом числе наблюдений и большом разбросе показателей 3) позволяет с помощью одного числа получить представления о совокупности массовых явлений 4) позволяет с помощью одного числа получить представления о распространенности массовых явлений
12. ЕДИНИЦА НАБЛЮДЕНИЯ ОПРЕДЕЛЯЕТСЯ В ЗАВИСИМОСТИ ОТ 1) программы исследования 2) плана исследования 3) цели и задач исследования 4) количества наблюдений
13. ВАРИАЦИОННЫЙ РЯД – ЭТО 1) ряд числовых измерений признака, расположенных в ранговом порядке и характеризующихся определенной частотой 2) ряд цифровых значений различных признаков 3) генеральная совокупность 4) ряд чисел, отражающих частоту (повторяемость) цифровых значений изучаемого признака
14. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ – ЭТО 1) варианта с наибольшей частотой 2) разность между наибольшей и наименьшей величиной 3) обобщающая величина, характеризующая размер варьи-рующего признака совокупности 4) варианта, находящаяся в середине ряда
15. МЕДИАНА – ЭТО 1) варианта с наибольшей частотой 2) разность между наибольшей и наименьшей величиной 3) обобщающая величина, характеризующая размер варьи-рующего признака совокупности 4) варианта, находящаяся в середине ряда
16. МОДА – ЭТО 1) варианта с наибольшей частотой 2) разность между наибольшей и наименьшей величиной 3) обобщающая величина, характеризующая размер варьи-рующего признака совокупности 4) варианта, находящаяся в середине ряда
17. ПРОЦЕСС СЛУЧАЙНОГО ОТБОРА ДАННЫХ НАЗЫВАЕТСЯ 1) рандомизацией 2) выборкой 3) репрезентативностью 4) экспликацией
18. ПРИЗНАК: «НАЛИЧИЕ ИЛИ ОТСУТСТВИЕ БОЛЕЗНИ» ЯВЛЯЕТСЯ 1) количественным 2) непрерывным 3) дискретным 4) дихотомическим
19. ЗАВИСИМЫЙ ПРИЗНАК, ИЗМЕНЯЮЩИЙ СВОЕ ЗНАЧЕНИЕ ПОД ВЛИЯНИЕМ ДРУГОГО, НАЗЫВАЕТСЯ 1) факторный 2) результативный 3) дискретный 4) непрерывный
20. ШКАЛА, УКАЗЫВАЮЩАЯ СТЕПЕНЬ ВЫРАЖЕННОСТИ ПРИЗНАКА 1) номинальная 2) интервальная 3) порядковая 4) логарифмическая
21. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ СОСТОИТ ИЗ 1) отдельных единиц наблюдения, взятых в известных границах времени и пространства 2) всех единиц наблюдения, которые могут быть отнесены к ней в соответствии с целью исследования 3) всех единиц наблюдения, которые могут быть отнесены к ней независимо от цели исследования 4) всех единиц наблюдения, обладающих определенным признаком
22. ОДНОЙ ИЗ СРЕДНИХ ВЕЛИЧИН ЯВЛЯЕТСЯ 1) показатель соотношения 2) медиана 3) среднее квадратическое отклонение 4) интенсивный показатель
23. ОТНОШЕНИЕ СУММЫ ЗНАЧЕНИЙ ВСЕХ ВАРИАНТ К ОБЩЕМУ ИХ КОЛИЧЕСТВУ – ЭТО 1) медиана 2) средняя арифметическая 3) мода 4) среднее квадратическое отклонение
24. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА ПРИМЕНЯЕТСЯ В ЦЕЛЯХ 1) обобщения числовых характеристик варьирующего явления при разработке или сводке материала 2) обобщения качественных характеристик 3) сравнения и сопоставления явлений 4) разработки нормативов
25. ИЗ ПРИВЕДЕННЫХ СРЕДНИХ НАИБОЛЕЕ ЧАСТО В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ ИСПОЛЬЗУЮТСЯ 1) средняя геометрическая 2) средняя арифметическая 3) средняя гармоническая 4) средняя алгебраическая
26. ВЕЛИЧИНЫ, РАЗБИВАЮЩИЕ ВАРИАЦИОННЫЙ РЯД НА ОТДЕЛЬНЫЕ (ПО ВОЗМОЖНОСТИ РАВНЫЕ) ЧАСТИ, ЭТО 1) квантили 2) варианты 3) ошибки средних величин 4) уровни ряда
27. НА ЧЕТЫРЕ РАВНЫЕ ЧАСТИ ВАРИАЦИОННЫЙ РЯД РАЗДЕЛЯЮТ 1) медиана 2) терцили 3) квартили 4) процентили
28. ЕСЛИ ДВА СОСЕДНИХ ЗНАЧЕНИЯ ВАРИАЦИОННОГО РЯДА ИМЕЮТ ОДИНАКОВУЮ ЧАСТОТУ, ТО 1) ряд не имеет моды 2) мода равняется среднему арифметическому этих значений 3) вариационный ряд имеет две моды 4) модой является число, стоящее ближе к середине ряда
29. ЕСЛИ ДВА ЗНАЧЕНИЯ ВАРИАЦИОННОГО РЯДА, НЕ ЯВЛЯЮЩИЕСЯ СОСЕДНИМИ, ИМЕЮТ ОДИНАКОВУЮ ЧАСТОТУ, ТО 1) ряд не имеет моды 2) мода равняется среднему арифметическому этих значений 3) вариационный ряд имеет две моды 4) модой является число, стоящее ближе к середине ряда
30. В ЗАВИСИМОСТИ ОТ ВИДА СЛУЧАЙНОЙ ВЕЛИЧИНЫ РАЗЛИЧАЮТ СЛЕДУЮЩИЕ ВИДЫ ВАРИАЦИОННЫХ РЯДОВ 1) несгруппированный и сгруппированный 2) моментный и интервальный 3) дискретный и непрерывный 4) простой и сложный
31. КАЧЕСТВЕННЫЕ ДАННЫЕ, КОТОРЫЕ МОГУТ БЫТЬ ОТНЕСЕНЫ ТОЛЬКО К ДВУМ ПРОТИВОПОЛОЖНЫМ КАТЕГОРИЯМ, ПРИНИМАЮЩИЕ ОДНО ИЗ ДВУХ ЗНАЧЕНИЙ, НАЗЫВАЮТСЯ 1) дискретные 2) дихотомическими 3) количественными 4) непрерывные
32. КОЛИЧЕСТВЕННЫЕ ПРИЗНАКИ, ПРИНИМАЮЩИЕ ЗНАЧЕНИЯ ЛИШЬ ИЗ НЕКОТОРОГО СПИСКА ОПРЕДЕЛЕННЫХ ЧИСЕЛ, ОБЫЧНО ЦЕЛЫХ, НАЗЫВАЮТСЯ 1) непрерывными 2) дихотомическими 3) случайными 4) дискретными
33. РЯД ПОСЛЕДОВАТЕЛЬНЫХ ЗНАЧЕНИЙ, ХАРАКТЕРИЗУЮЩИХ ИЗМЕНЕНИЕ ПОКАЗАТЕЛЯ ВО ВРЕМЕНИ, И ИМЕЮЩИЙ СОДЕРЖАТЕЛЬНЫЙ СМЫСЛ, ЭТО 1) временной срез 2) временной ряд 3) произвольный ряд 4) вариационный ряд
34. ДАННЫЕ, СОДЕРЖАЩИЕ ИНФОРМАЦИЮ О ТРЕХ ИЛИ БОЛЕЕ ПРИЗНАКАХ ДЛЯ КАЖДОГО ОБЪЕКТА, НАЗЫВАЮТСЯ 1) одномерные 2) двумерные 3) многомерные 4) множественные
35. КАЖДОЕ ЧИСЛОВОЕ ЗНАЧЕНИЕ В ВАРИАЦИОННОМ РЯДУ НАЗЫВАЮТ 1) вариантой 2) случаем 3) медианой 4) модой
36. ПРИ ПРАВОСТОРОННЕЙ АСИММЕТРИИ СЛЕВА НАПРАВО РАСПОЛОЖЕНЫ 1) мода, медиана и среднее арифметическое совпадают 2) мода, далее медиана, затем среднее арифметическое 3) среднее арифметическое, далее медиана, потом мода 4) среднее арифметическое, мода, медиана
37. ЕСЛИ ГРАФИК РАСПРЕДЕЛЕНИЯ ИМЕЕТ СИММЕТРИЧНУЮ ФОРМУ, ТО 1) левее расположена мода, затем медиана и среднее арифметическое 2) левее расположена среднее арифметическое, затем медиана и мода 3) левее расположено среднее арифметическое, затем мода и медиана 4) мода, медиана и среднее арифметическое совпадают
38. ЕСЛИ ВСЕ ЗНАЧЕНИЯ В ВАРИАЦИОННОМ РЯДУ ВСТРЕЧАЮТСЯ ОДИНАКОВО ЧАСТО, СЧИТАЕТСЯ, ЧТО ЭТОТ РЯД 1) не имеет моды 2) имеет две моды 3) имеет одну моду 4) имеет три моды
39. КОЛИЧЕСТВЕННЫЕ ПРИЗНАКИ, ПРИНИМАЮЩИЕ ЛЮБОЕ ЗНАЧЕНИЕ НА НЕПРЕРЫВНОЙ ШКАЛЕ, НАЗЫВАЮТСЯ 1) дискретные 2) случайные 3) непрерывные 4) порядковые
40. РЕПРЕЗЕНТАТИВНОСТЬ, ОБОЗНАЧАЮЩАЯ СТРУКТУРНОЕ СООТВЕТСТВИЕ ВЫБОРОЧНОЙ И ГЕНЕРАЛЬНОЙ СОВОКУПНОСТЕЙ, НАЗЫВАЕТСЯ 1) количественной 2) качественной 3) выборочной 4) случайной
Эталоны ответов к тестовым заданиям:
Дата добавления: 2014-12-11 | Просмотры: 3544 | Нарушение авторских прав |
чайный характер, а также совместное воздействие на изучаемое явление небольшого числа случайно сочетающихся факторов. Однако, если какой-либо фактор играет преобладающую роль, то распределение не будет подчиняться Гауссову закону. Например, при исследовании показателя сахара крови для больных сахарным диабетом кривая распределения, имеющая симметричную форму для совокупности здоровых пациентов, станет несимметричной, и ее максимум сместится вправо (левостороннее асимметричное распределение).
) – правее медианы: